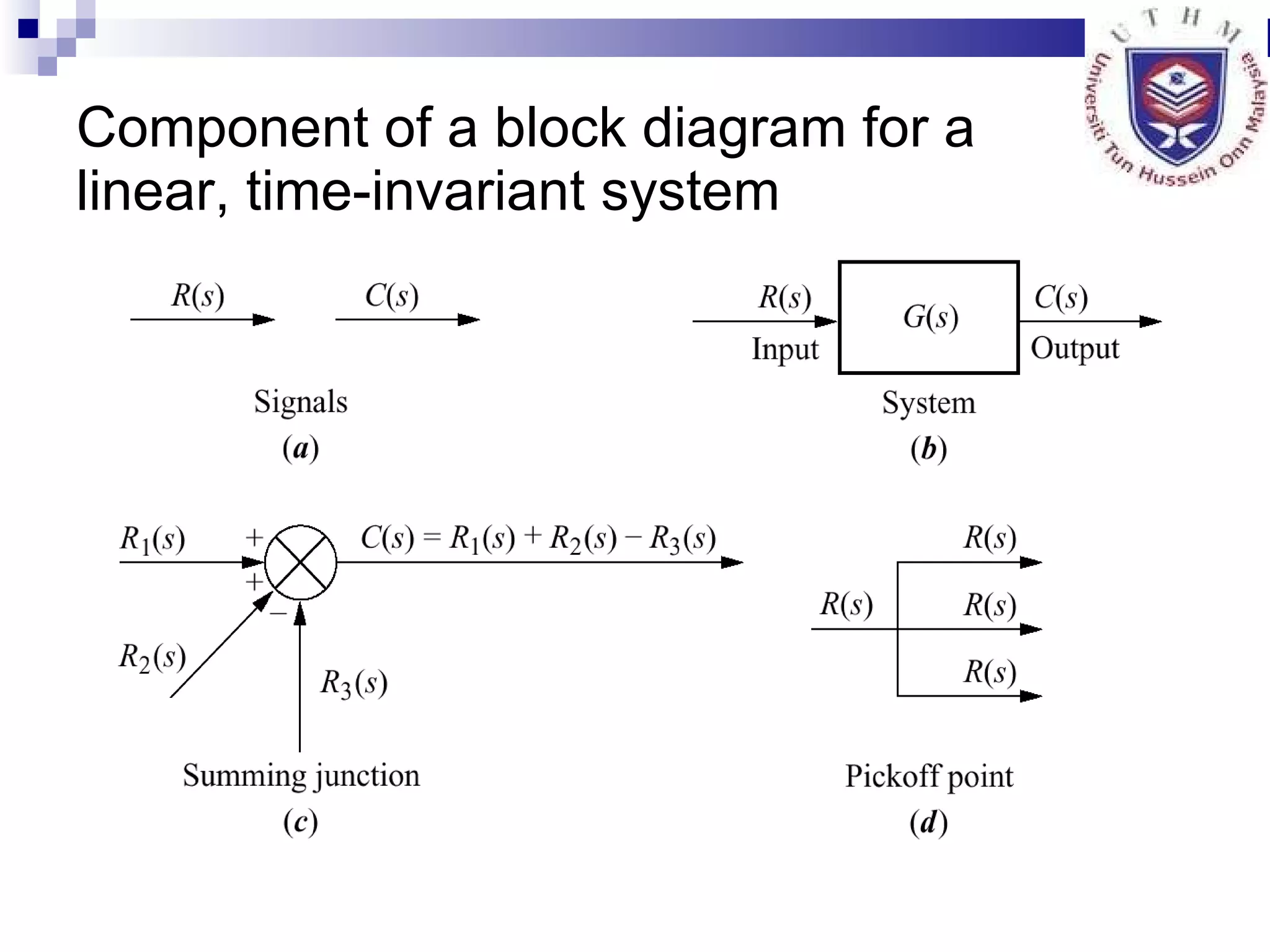
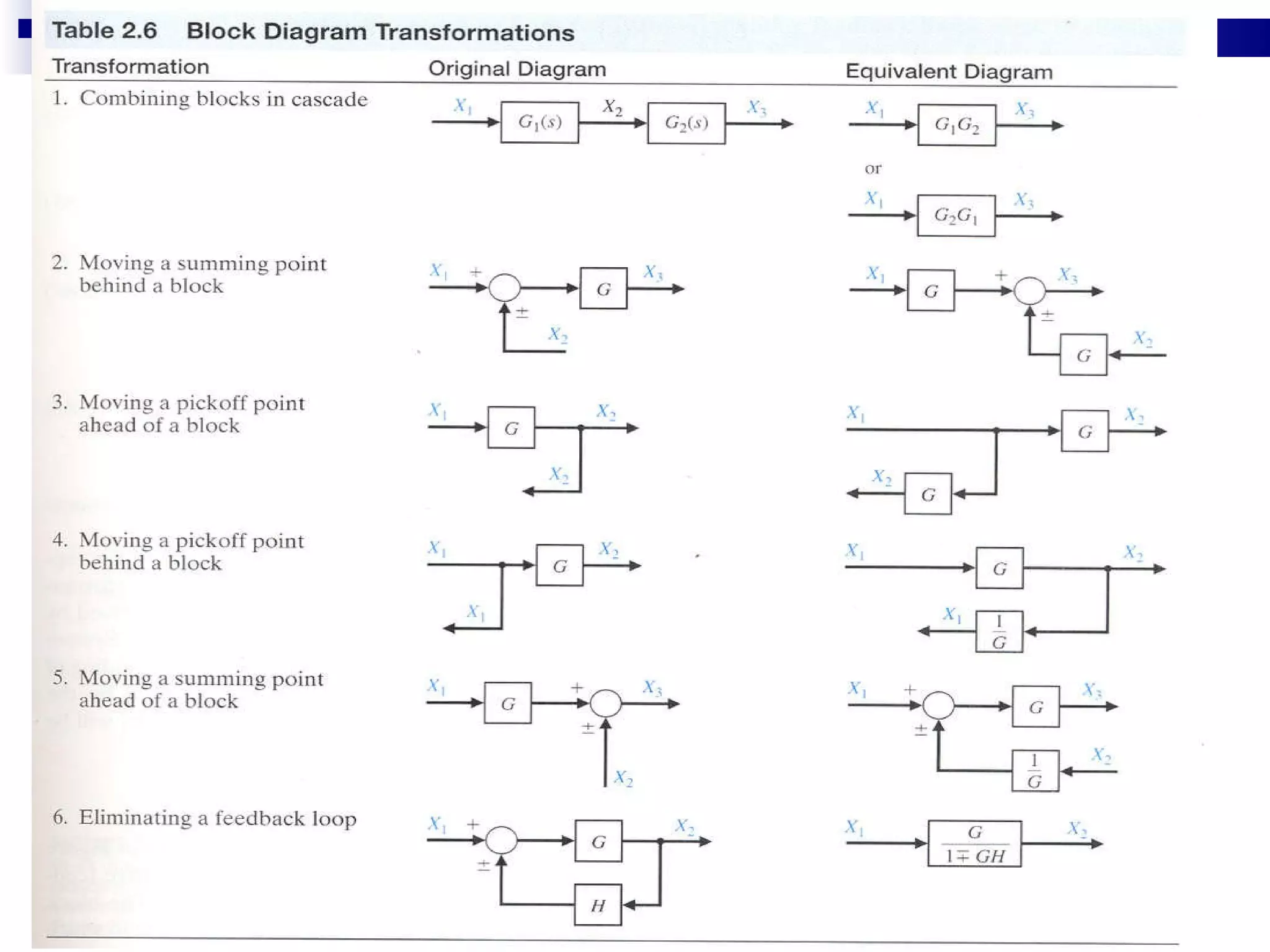
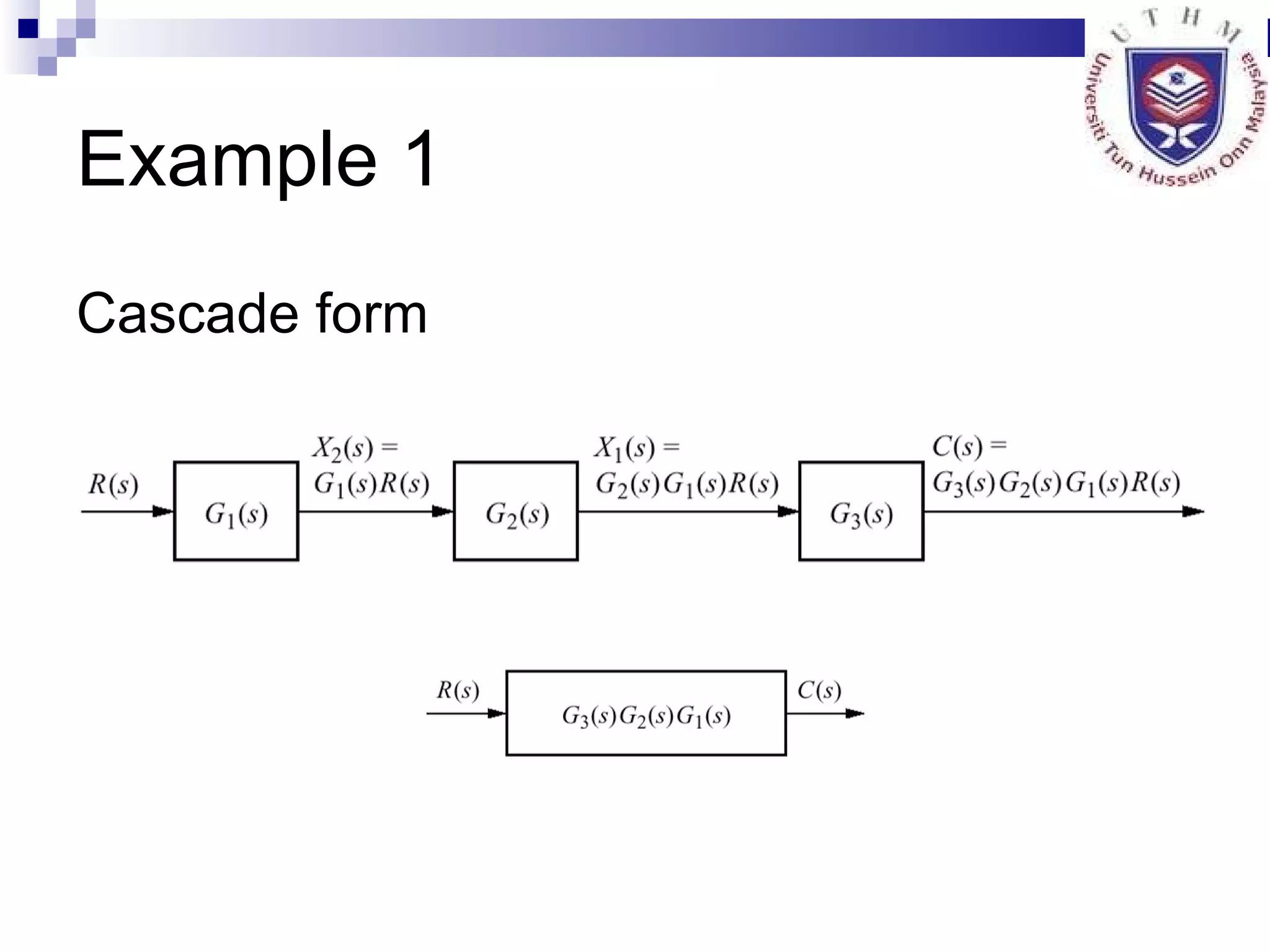
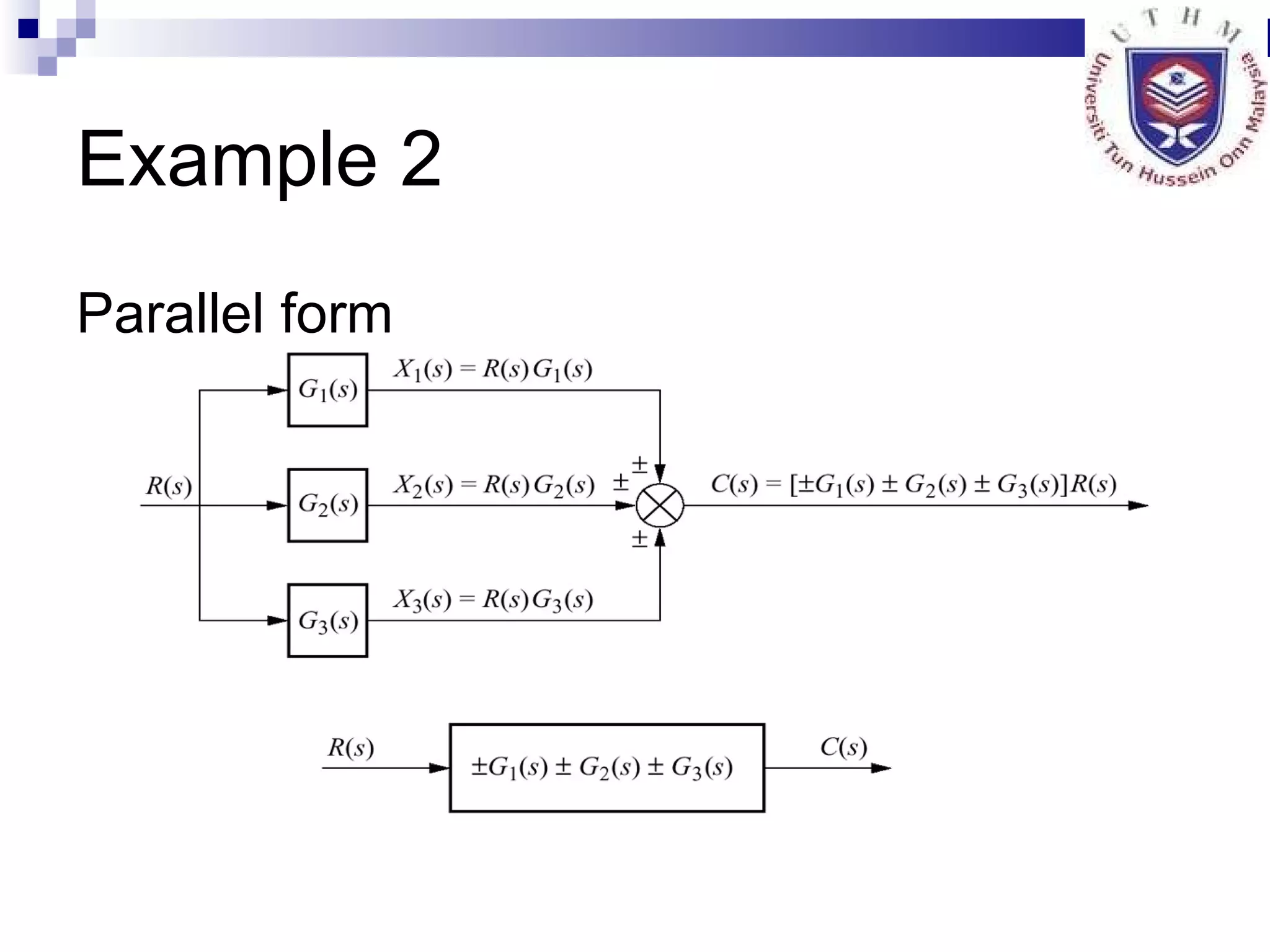
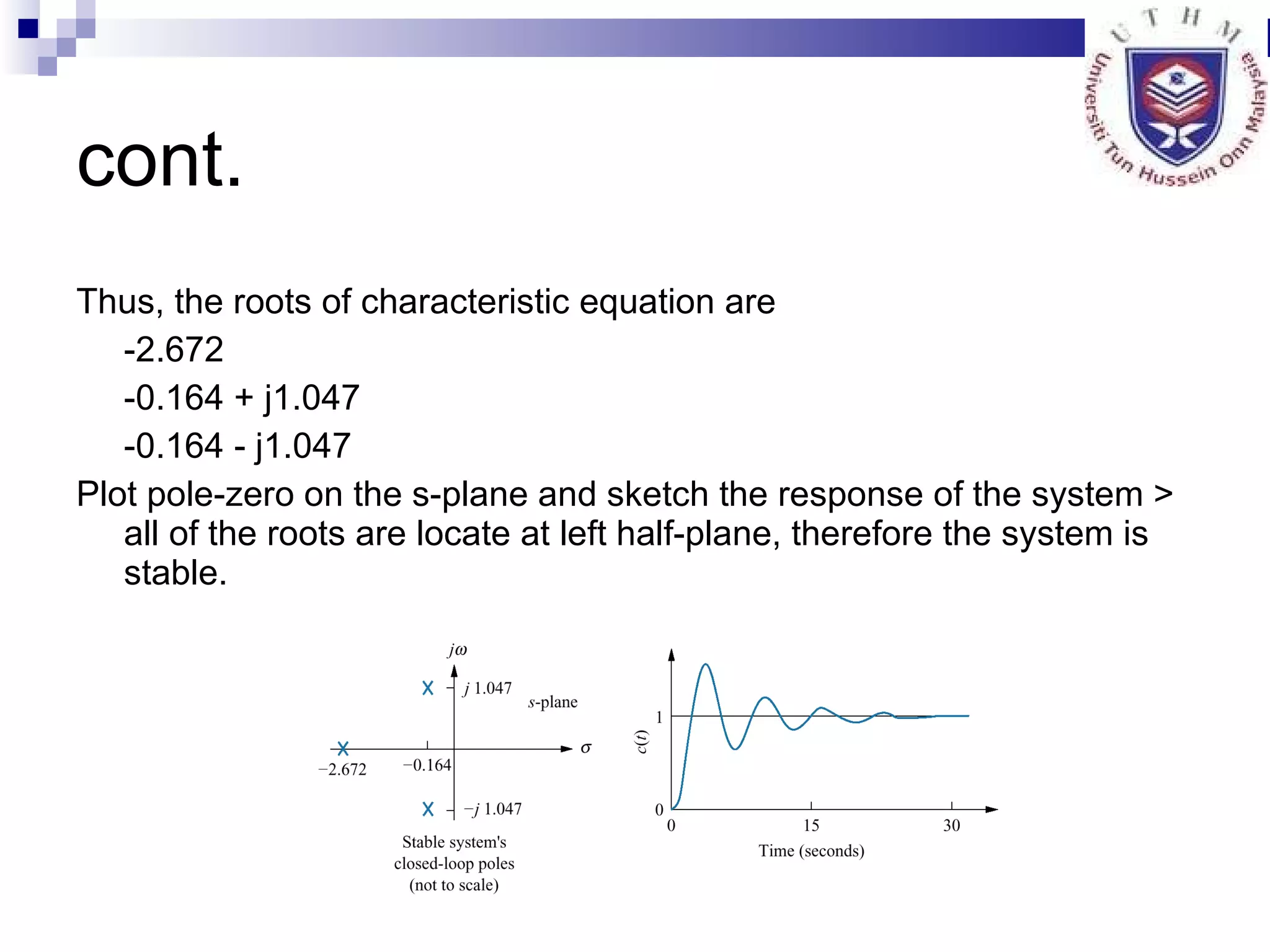
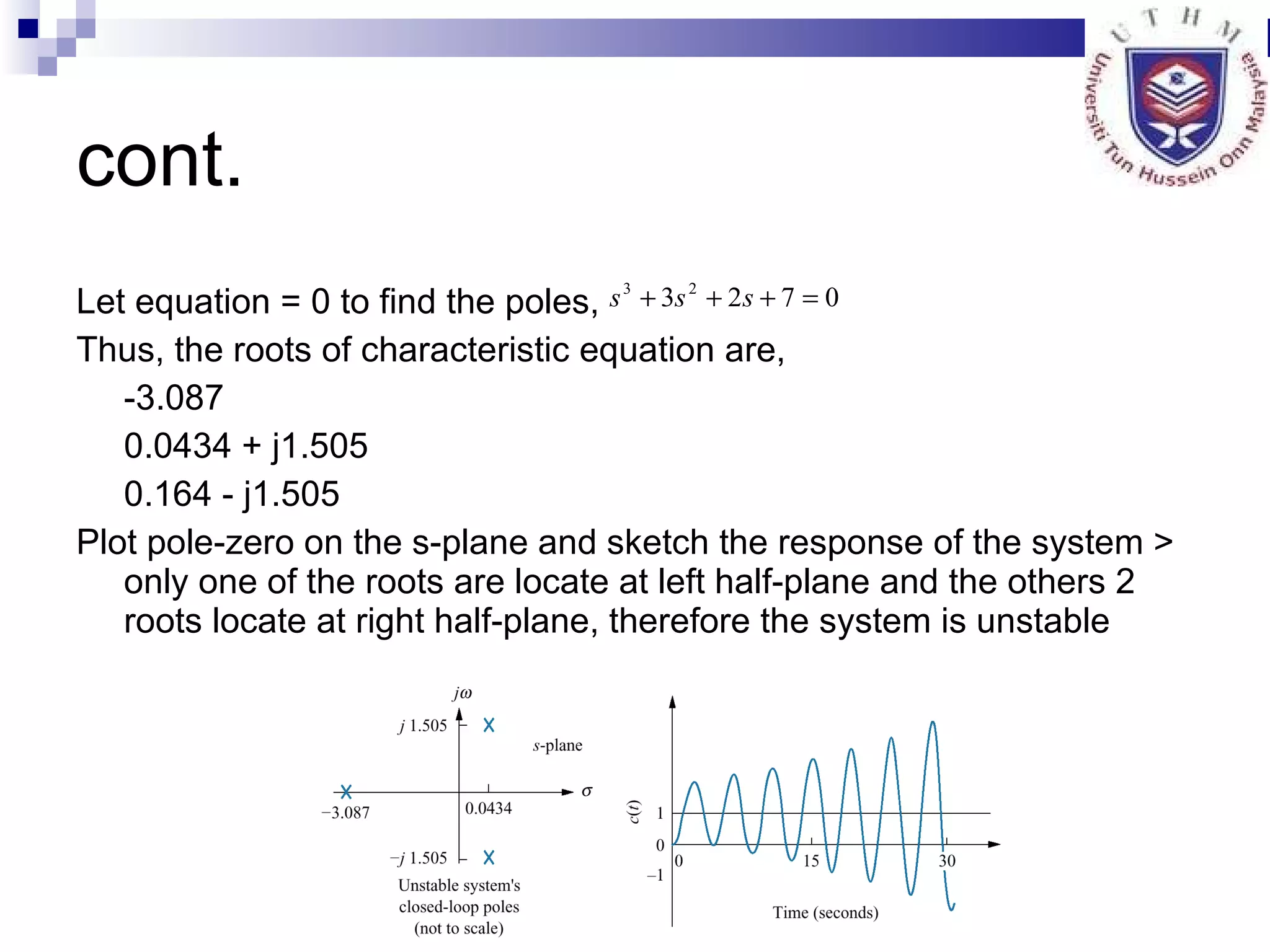
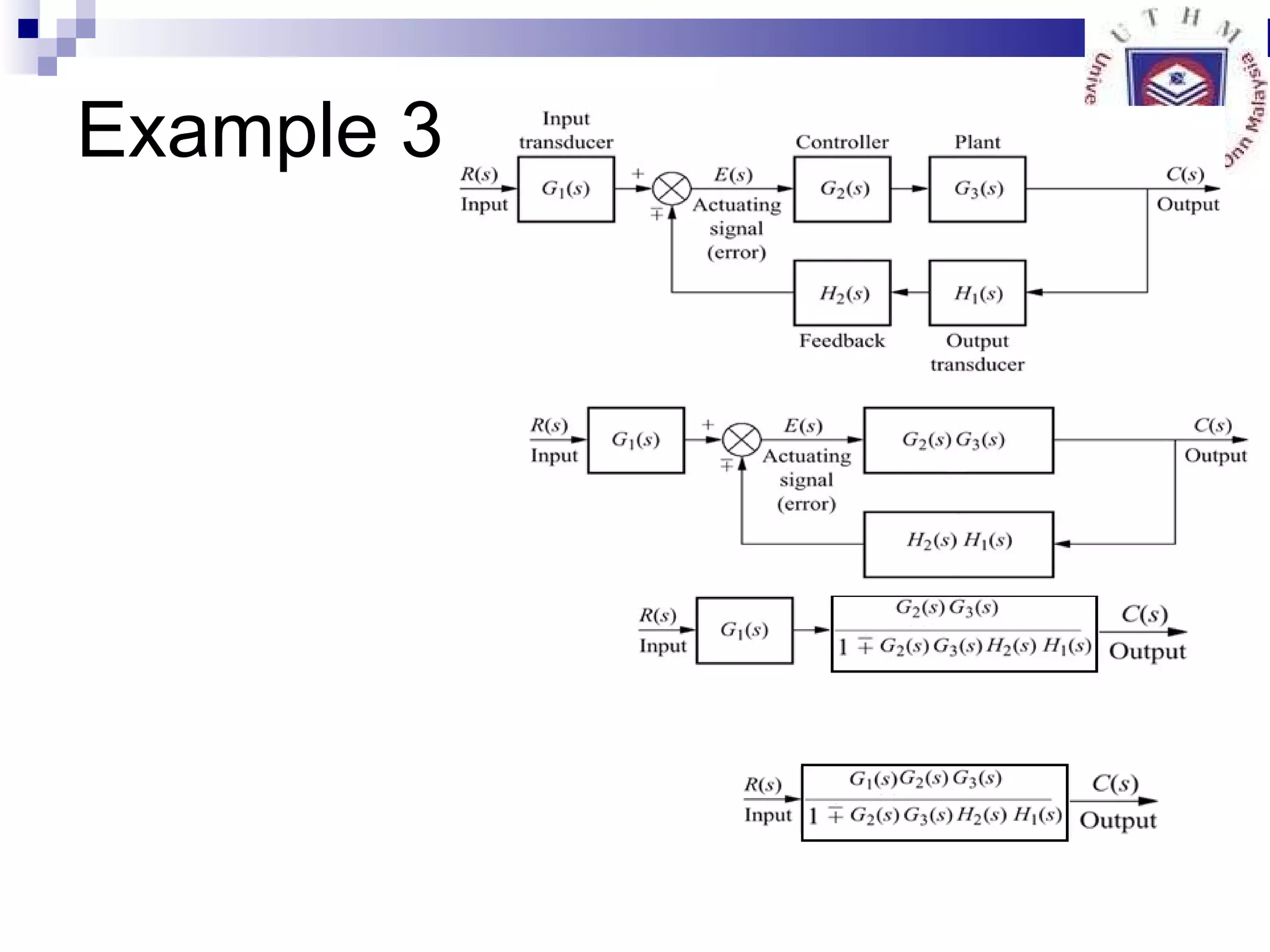
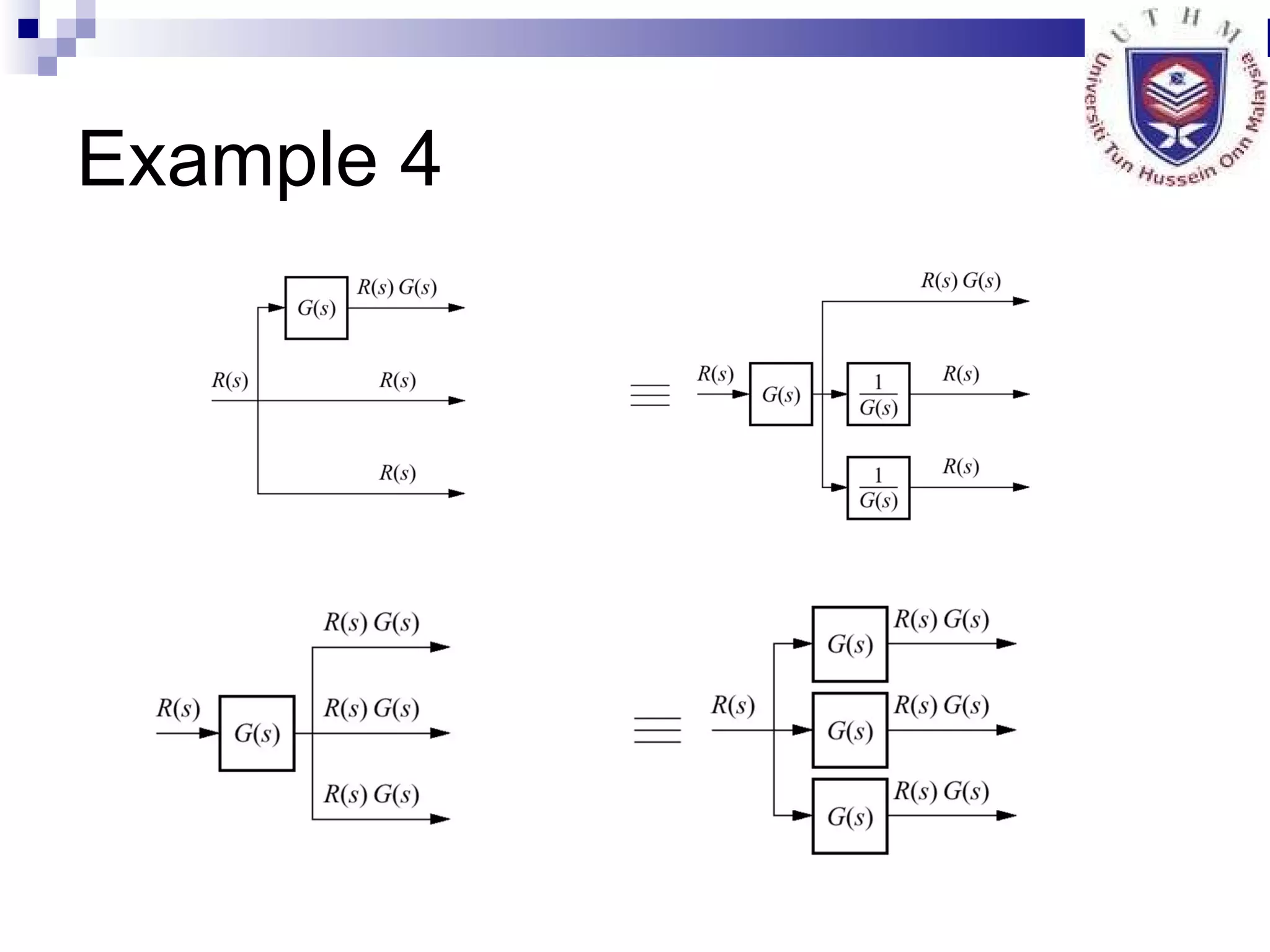
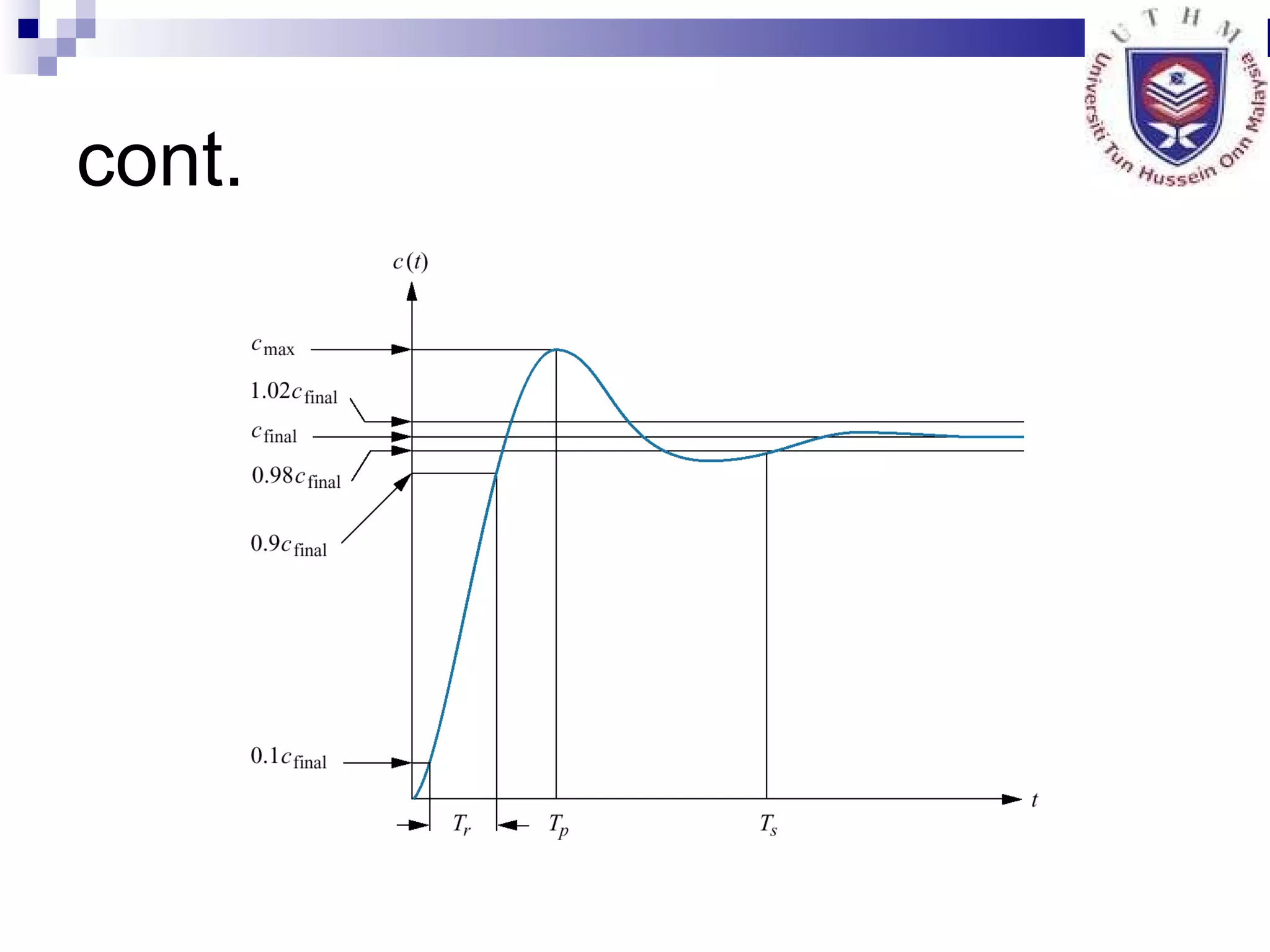
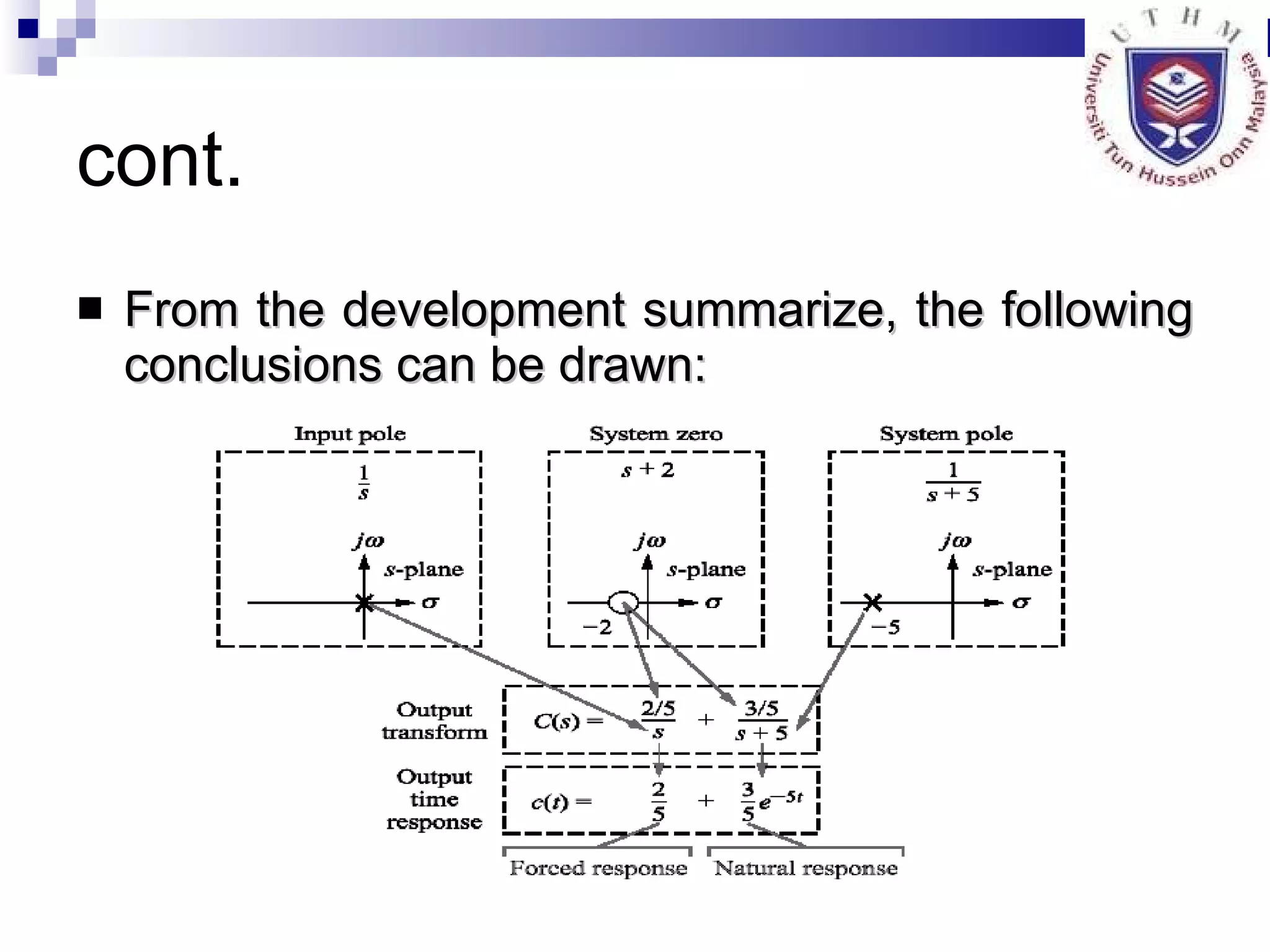
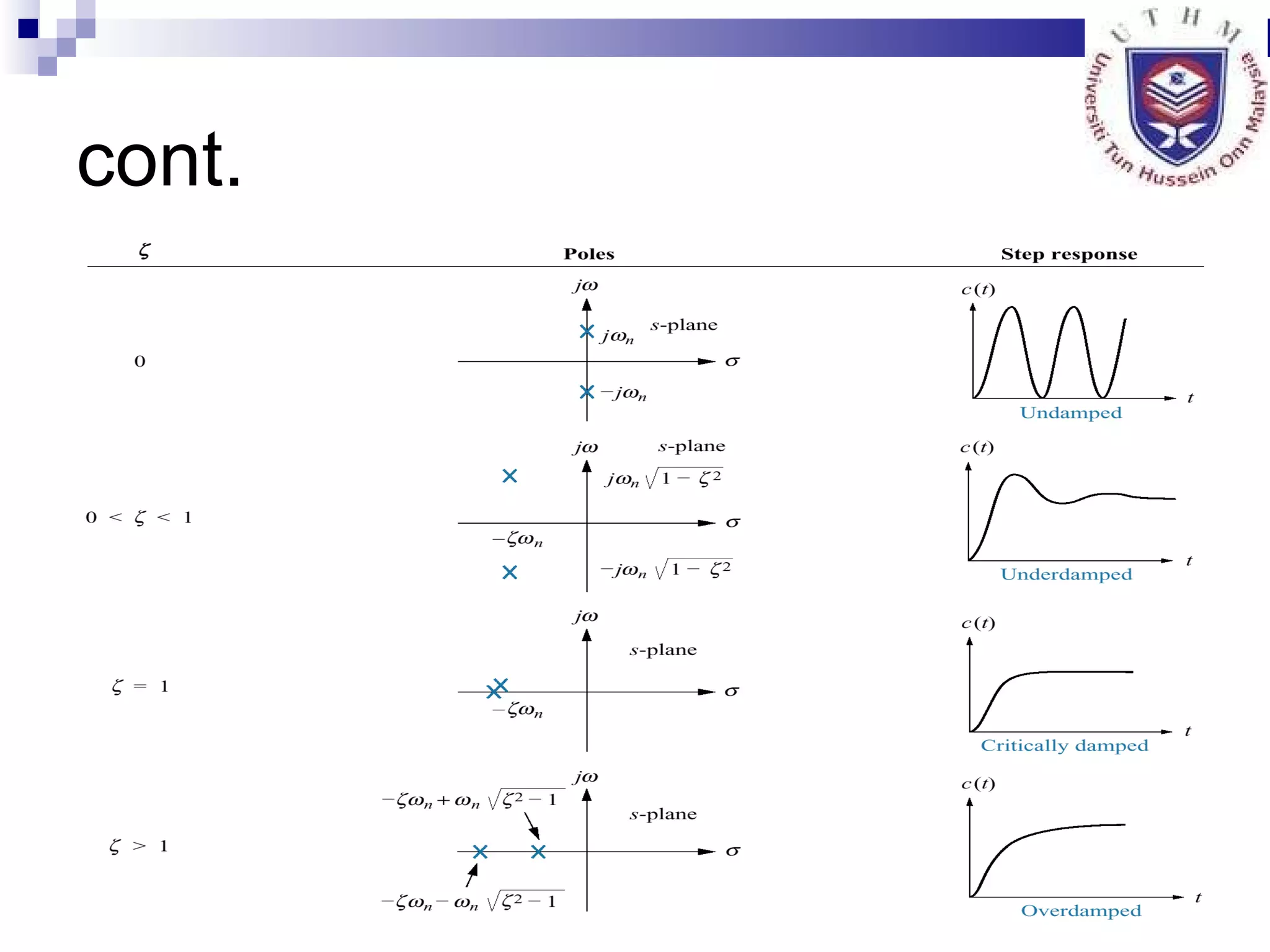
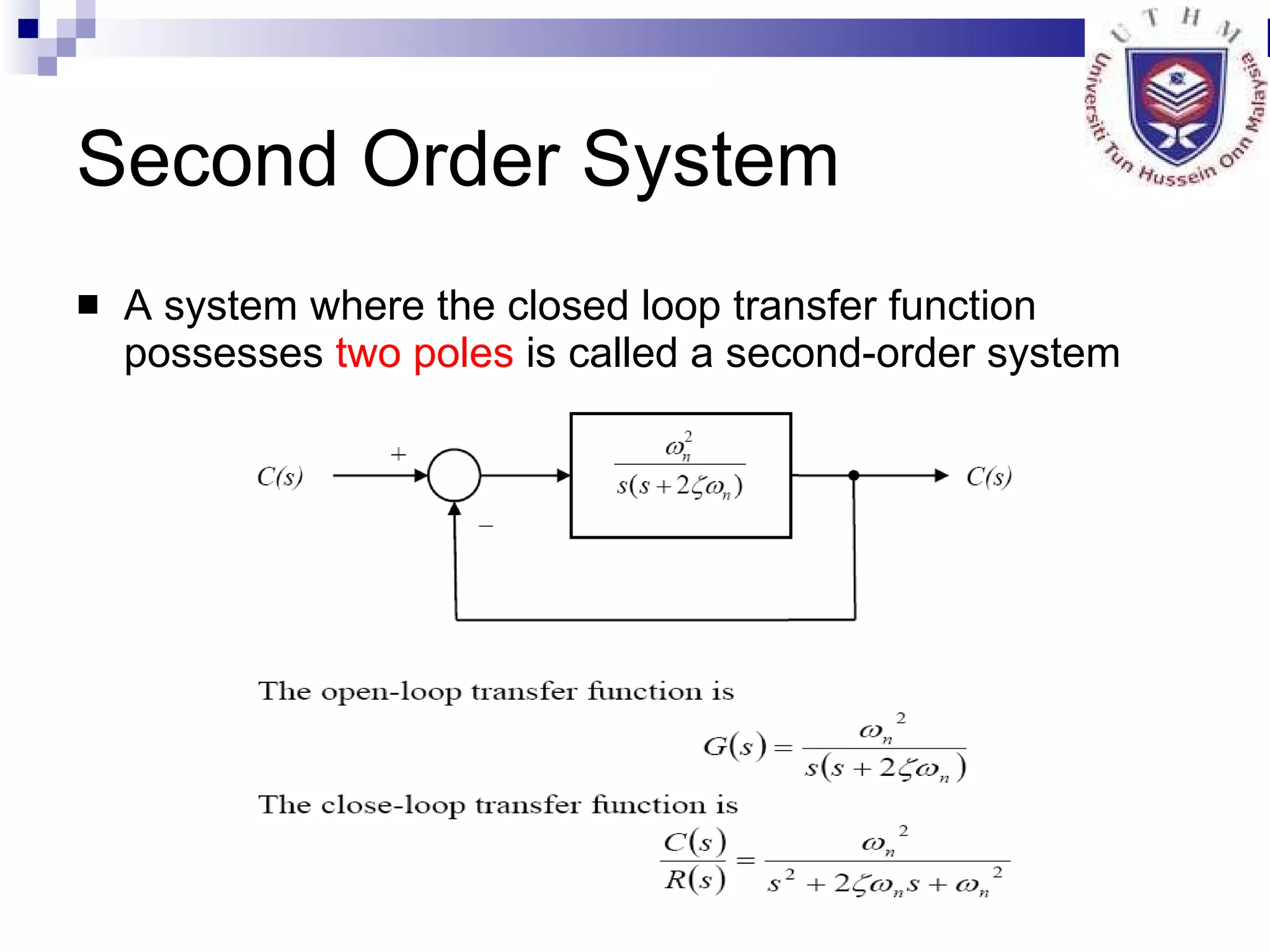
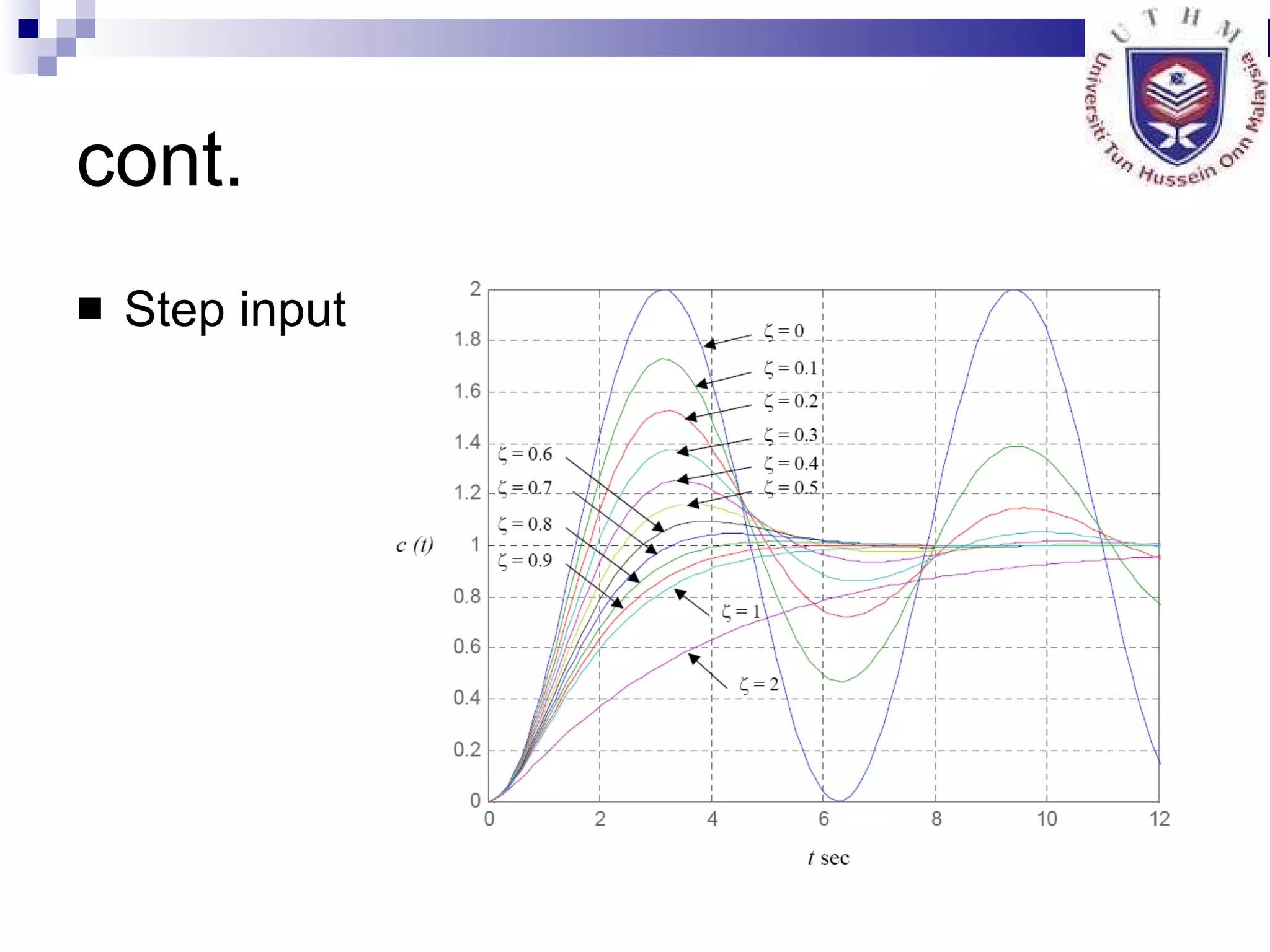
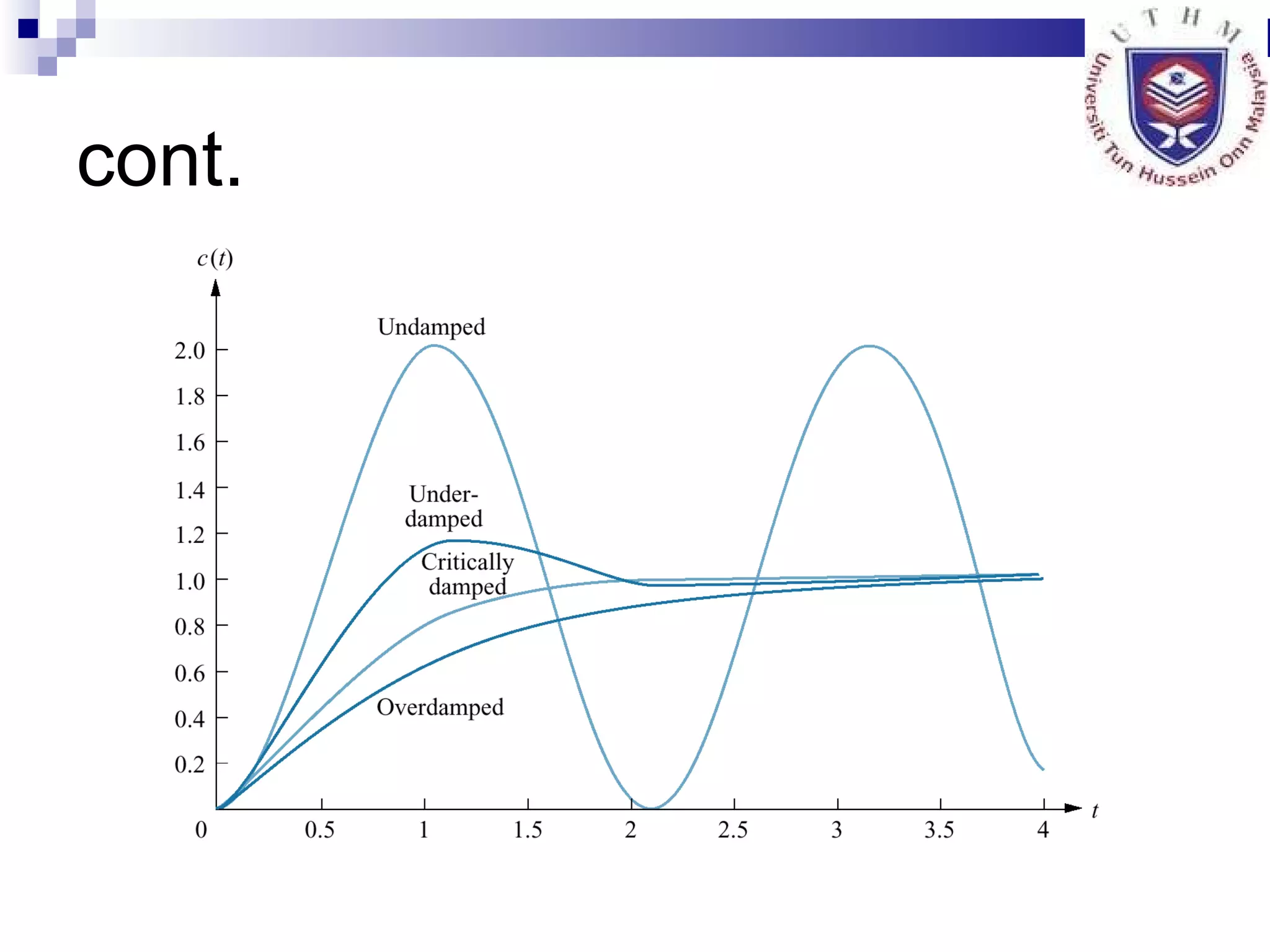
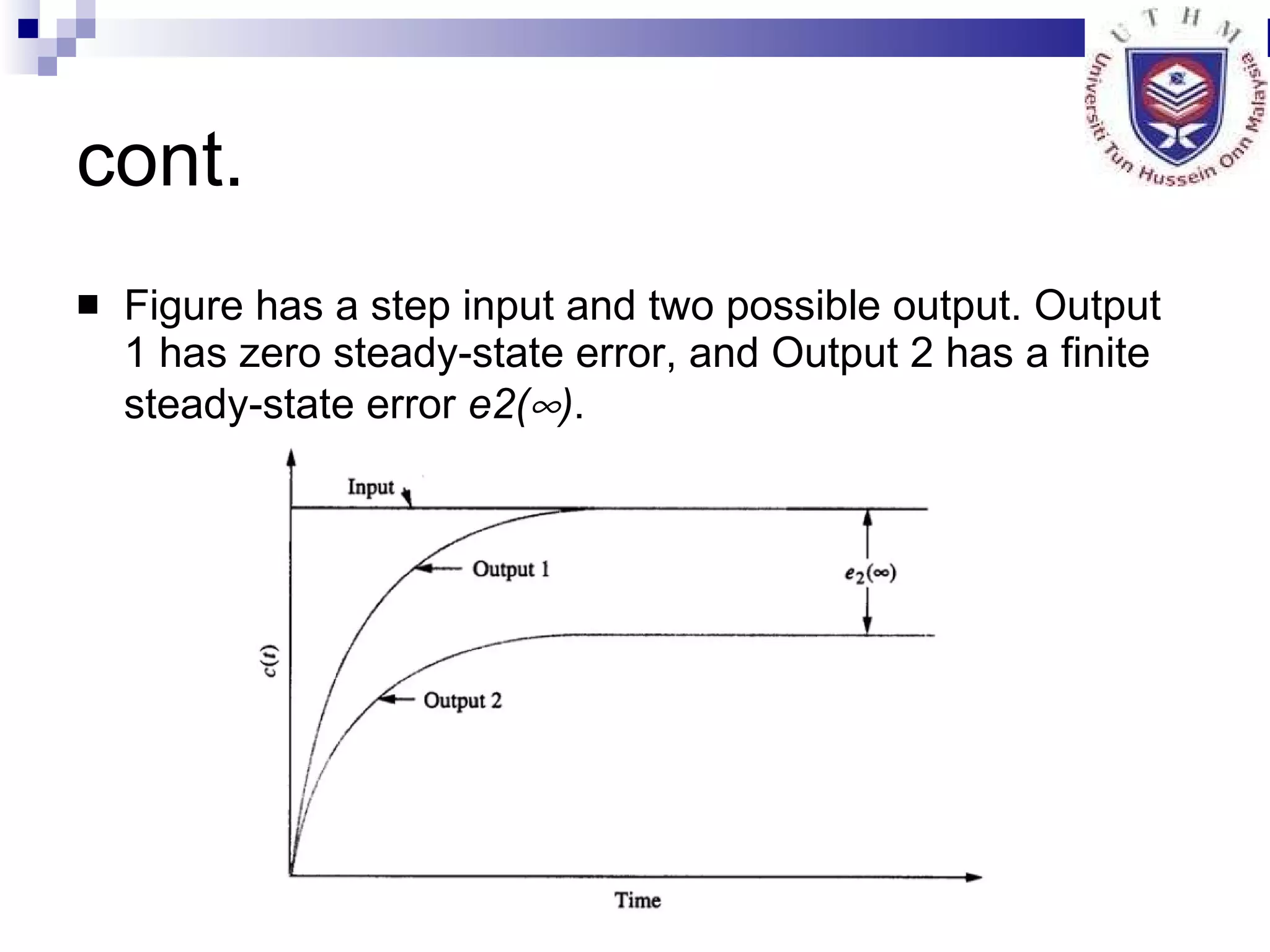
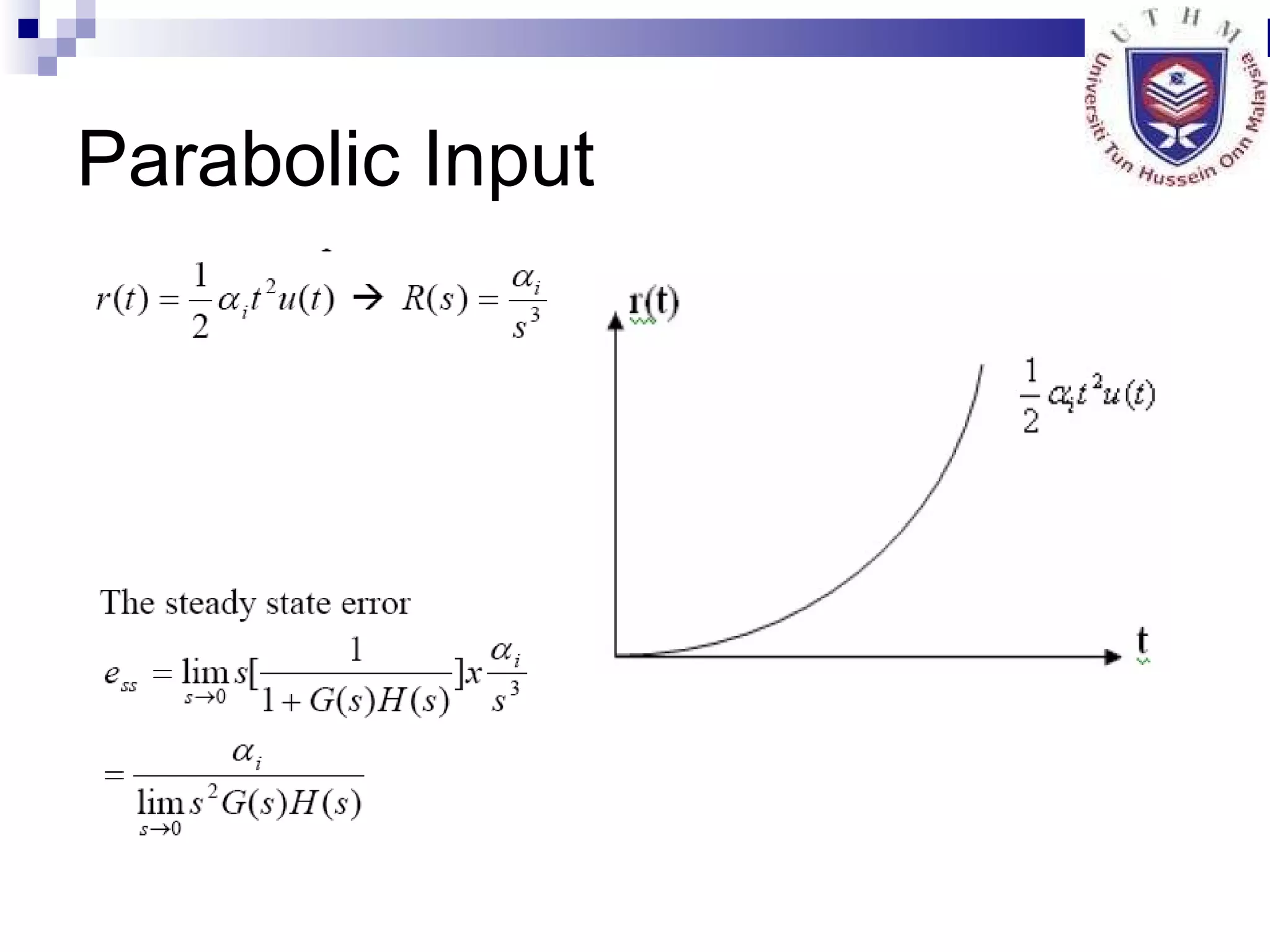
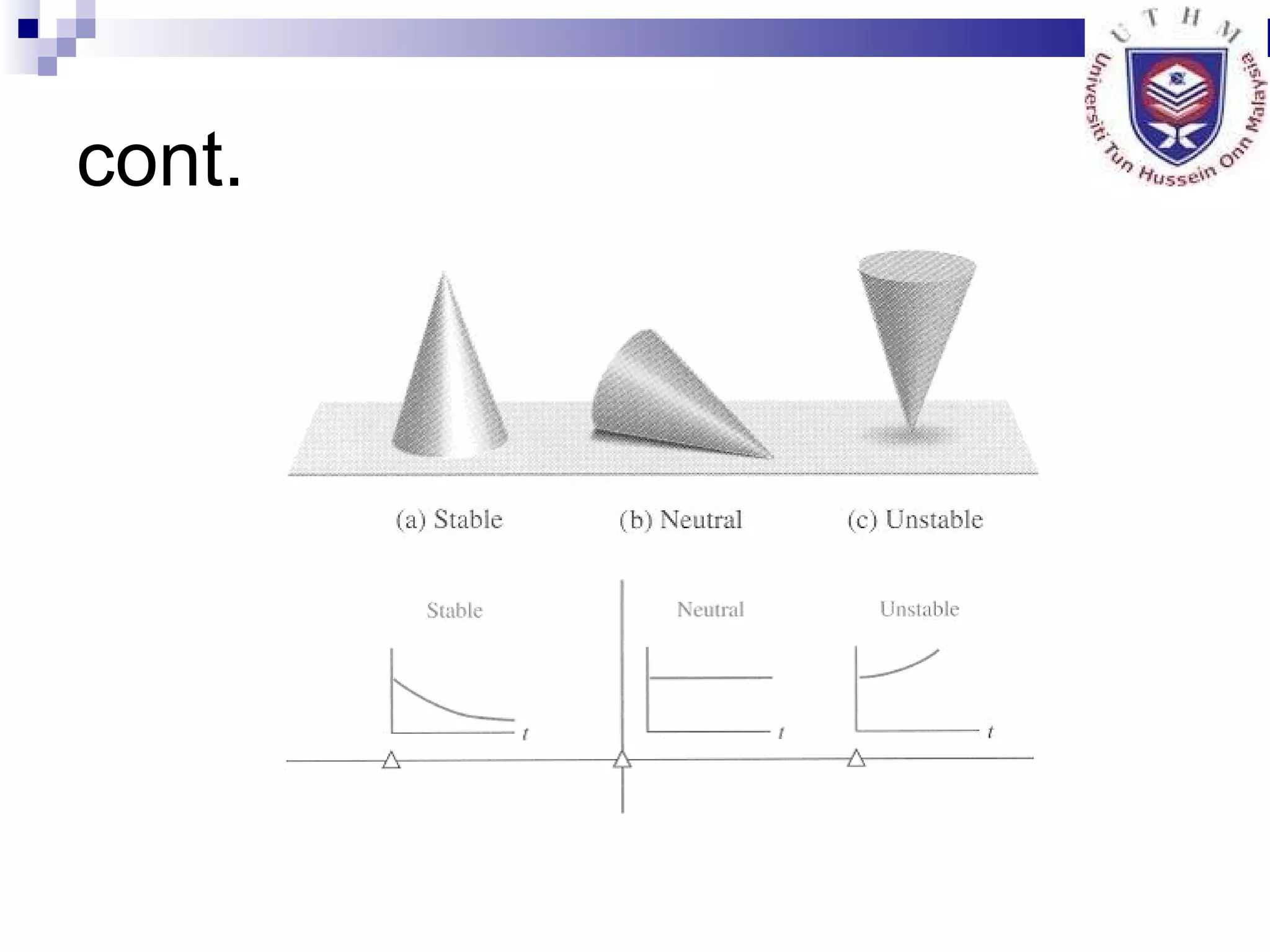
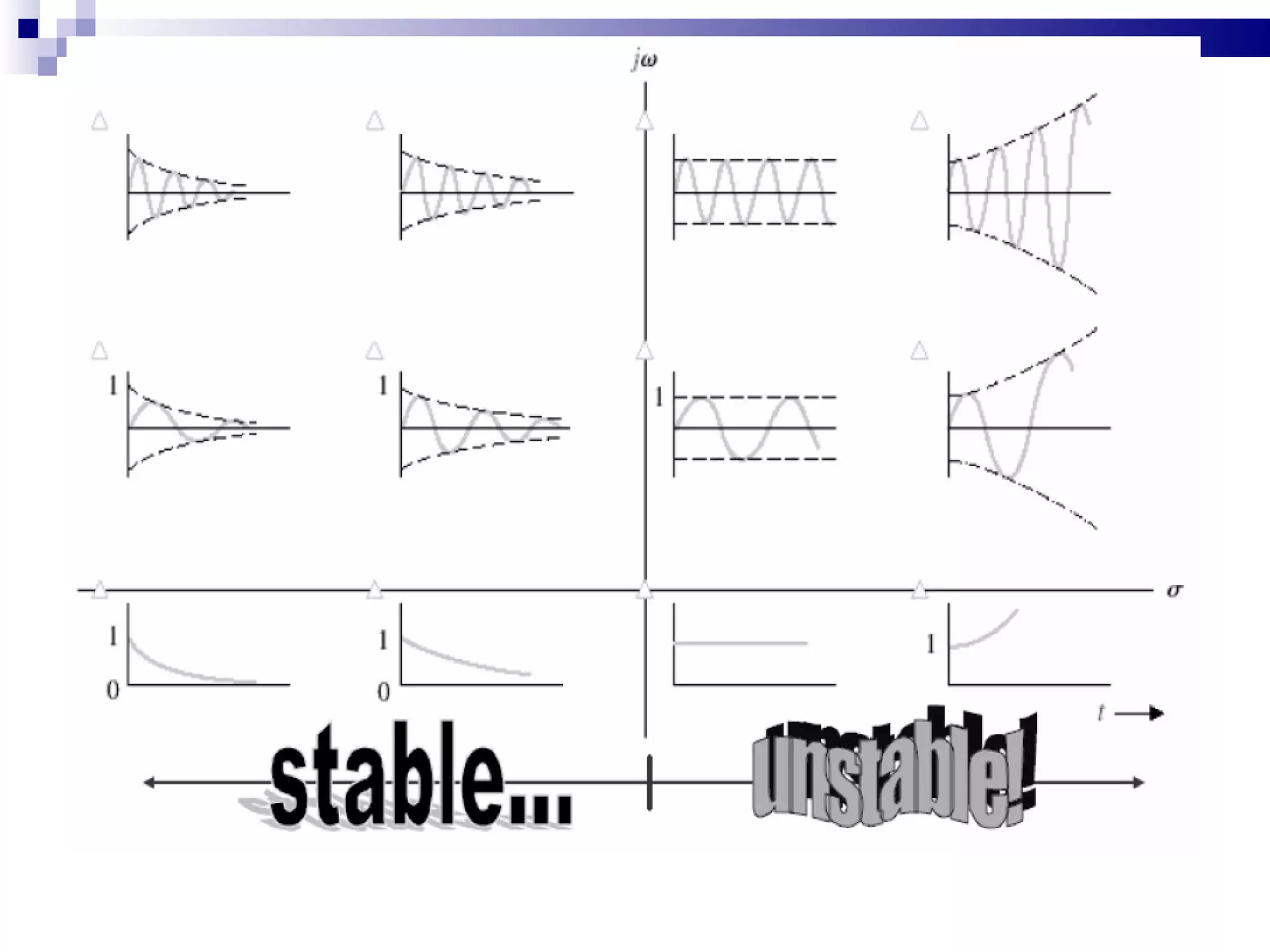
The document discusses multiple topics related to analog control systems, including: 1. Reducing multiple subsystems into a single block to simplify analysis. 2. Describing system response in terms of transient and steady state response. 3. Explaining poles, zeros and how they relate to system response. 4. Defining characteristics of second order systems and analyzing steady state error. 5. Discussing stability analysis in the complex s-plane and conditions for stable, unstable and marginally stable systems.

3. Component of a block diagram for a linear, time-invariant system

7. Example 3

8. Example 4

16. cont.

18. cont.

19. cont.

20. cont.

23. cont.

27. Step input

28. Ramp Input

29. Parabolic Input

32. cont.