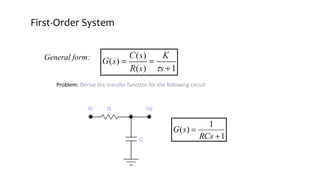
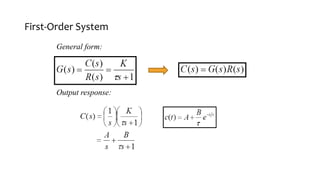
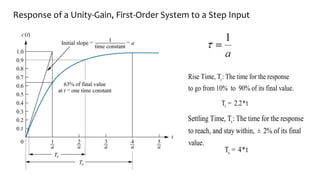
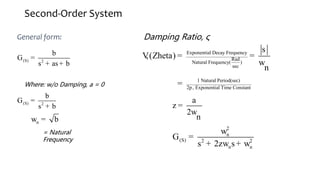
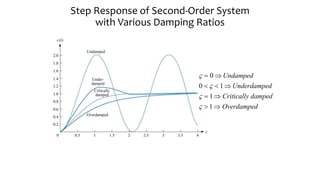
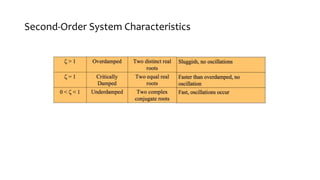
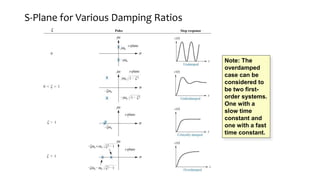
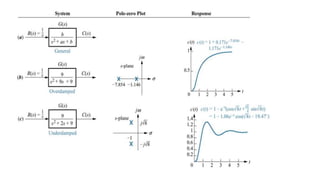
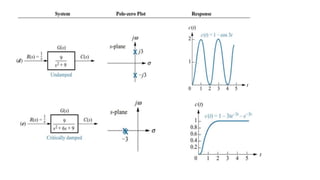
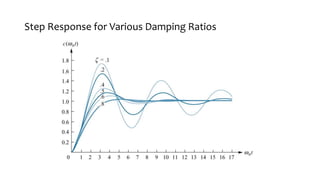
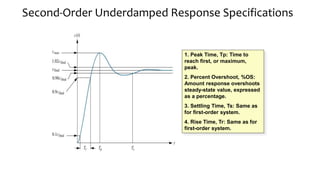
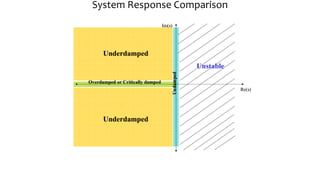
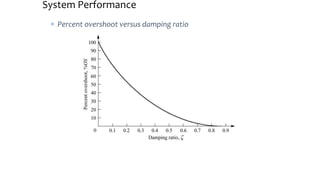
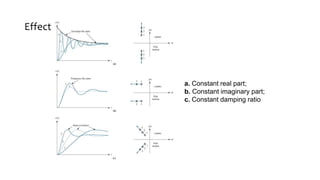
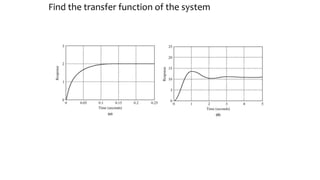
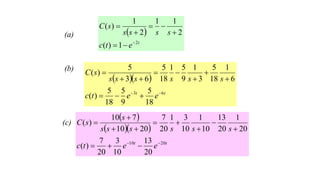This document discusses time response characteristics of first-order and second-order systems. It defines key terms like poles, zeros, damping ratio, natural frequency that determine the system response. Specific topics covered include influence of pole locations on response, specifications for transient response, comparison of underdamped vs overdamped vs critically damped systems. Worked examples calculate response parameters for various transfer functions. The document provides information on analyzing and characterizing linear system responses based on their pole-zero locations and configurations.