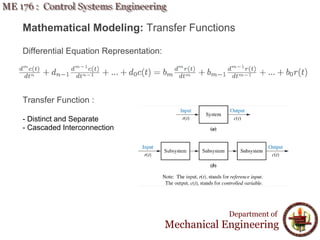
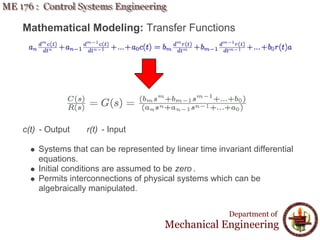
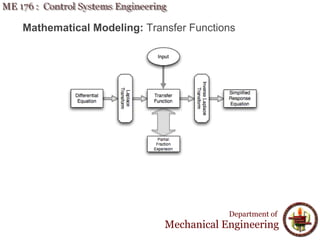
This document discusses mathematical modeling for control systems engineering. It introduces mathematical models as simplified representations of physical systems using assumptions. There are two common types of mathematical models: transfer functions in the frequency domain and state equations in the time domain. The document outlines steps for creating mathematical models using laws of physics and engineering, and describes various modeling techniques including transfer functions, Laplace transforms, and partial fraction expansions. It emphasizes that mathematical modeling permits representing physical systems as separate entities that can be algebraically manipulated.

1. ME 176
Control Systems Engineering
Department of
Mechanical Engineering
Mathematical Modeling

2. Mathematical Modeling: Introduction
Mathematical Models are representation of a system's schematics,
which in turn is a representation of a system simplified using
assumptions in order to keep the model manageable and still an
approximation of reality.
1. Transfer Functions (Frequency Domain)
2. State Equations (Time Domain)
First step in creating a mathematical model is applying the
fundamental laws of physics and engineering:
Electrical Networks - Ohm's law and Kirchhoff's laws
Mechanical Systems - Newton's laws.
Department of
Mechanical Engineering

3. Mathematical Modeling: Transfer Functions
Differential Equation Representation:
Transfer Function :
- Distinct and Separate
- Cascaded Interconnection
Department of
Mechanical Engineering

4. Mathematical Modeling: Laplace Transform
Represents relations of subsystems as separate entities.
Interrelationship are algebraic.
Laplace Transform:
Inverse Laplace Transform:
Department of
Mechanical Engineering

5. Mathematical Modeling: Laplace Transform
Department of
Mechanical Engineering
Laplace Transform Table
Unit Impulse
Unit Step
Ramp
Exponential
Decay
Sine
Cosine
Laplace Transform Theorems
Linearity
Frequency
Shift
Time
Shift
Scaling
Differentiation
Integration
Initial Value
Final Value

6. Mathematical Modeling: Laplace Transform
Partial Fraction Expansion, where roots of the Denominator of F(s) are:
Note: N(s) must be less order that D(s) .
1. Real and Distinct
where,
Department of
Mechanical Engineering

7. Mathematical Modeling: Laplace Transform
Partial Fraction Expansion, where roots of the Denominator of F(s) are:
2. Real and Repeated
where,
Department of
Mechanical Engineering

8. Mathematical Modeling: Laplace Transform
Partial Fraction Expansion, where roots of the Denominator of F(s) are:
3. Complex or Imaginary (Part 1) - compute for residues
Steps:
a. Solve for known residues.
b. Multiply by lowest common denominator
and clearing fractions.
c. Balancing coefficients.
Department of
Mechanical Engineering

9. Mathematical Modeling: Laplace Transform
Partial Fraction Expansion, where roots of the Denominator of F(s) are:
3. Complex or Imaginary (Part 2) - put into proper form
Steps:
a. Complete squares of denominator.
b. Adjust numerator.
Department of
Mechanical Engineering

10. Mathematical Modeling: Transfer Functions
c(t) - Output r(t) - Input
Systems that can be represented by linear time invariant differential
equations.
Initial conditions are assumed to be zero .
Permits interconnections of physical systems which can be
algebraically manipulated.
Department of
Mechanical Engineering

11. Mathematical Modeling: Transfer Functions
Department of
Mechanical Engineering