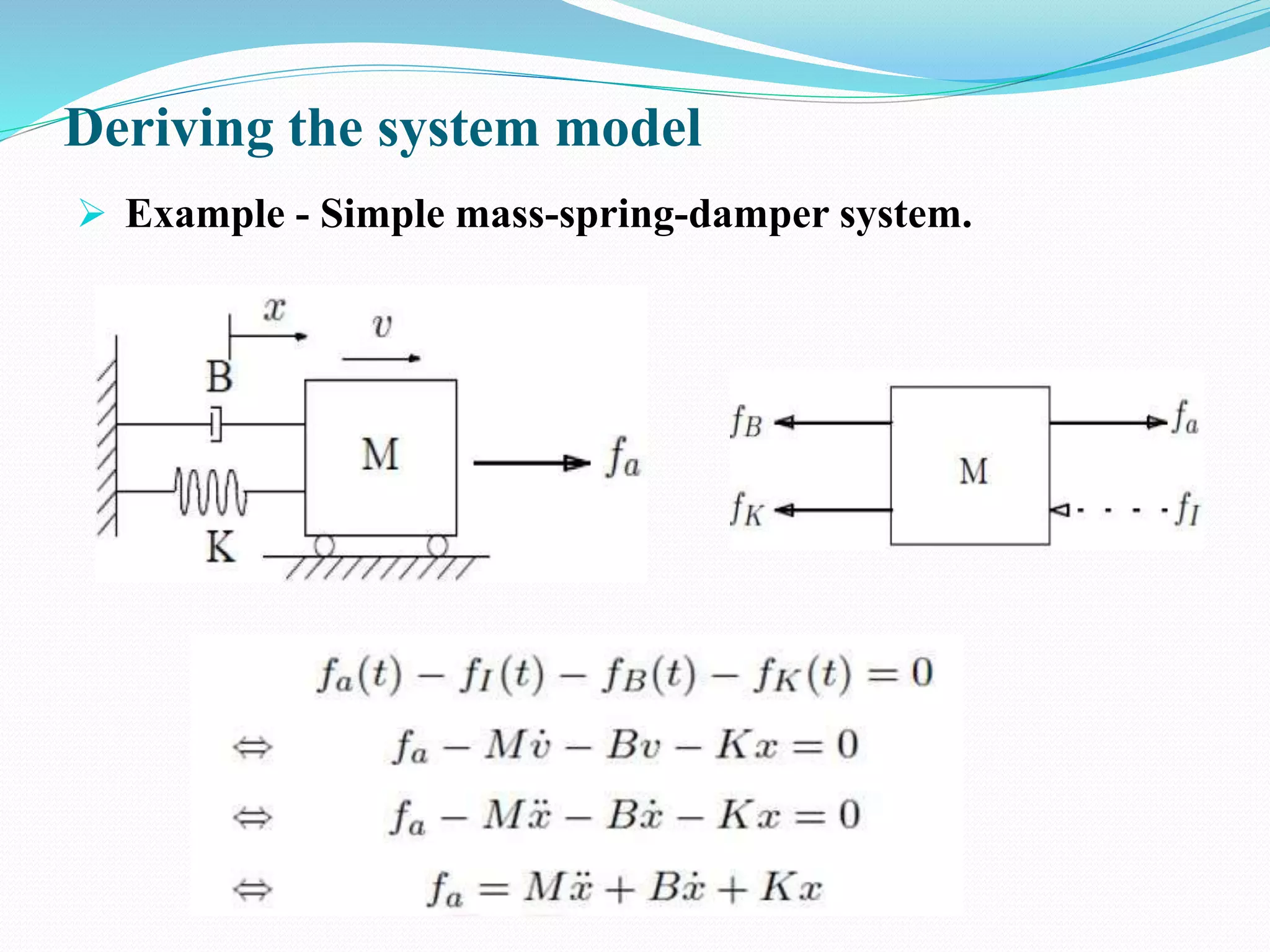
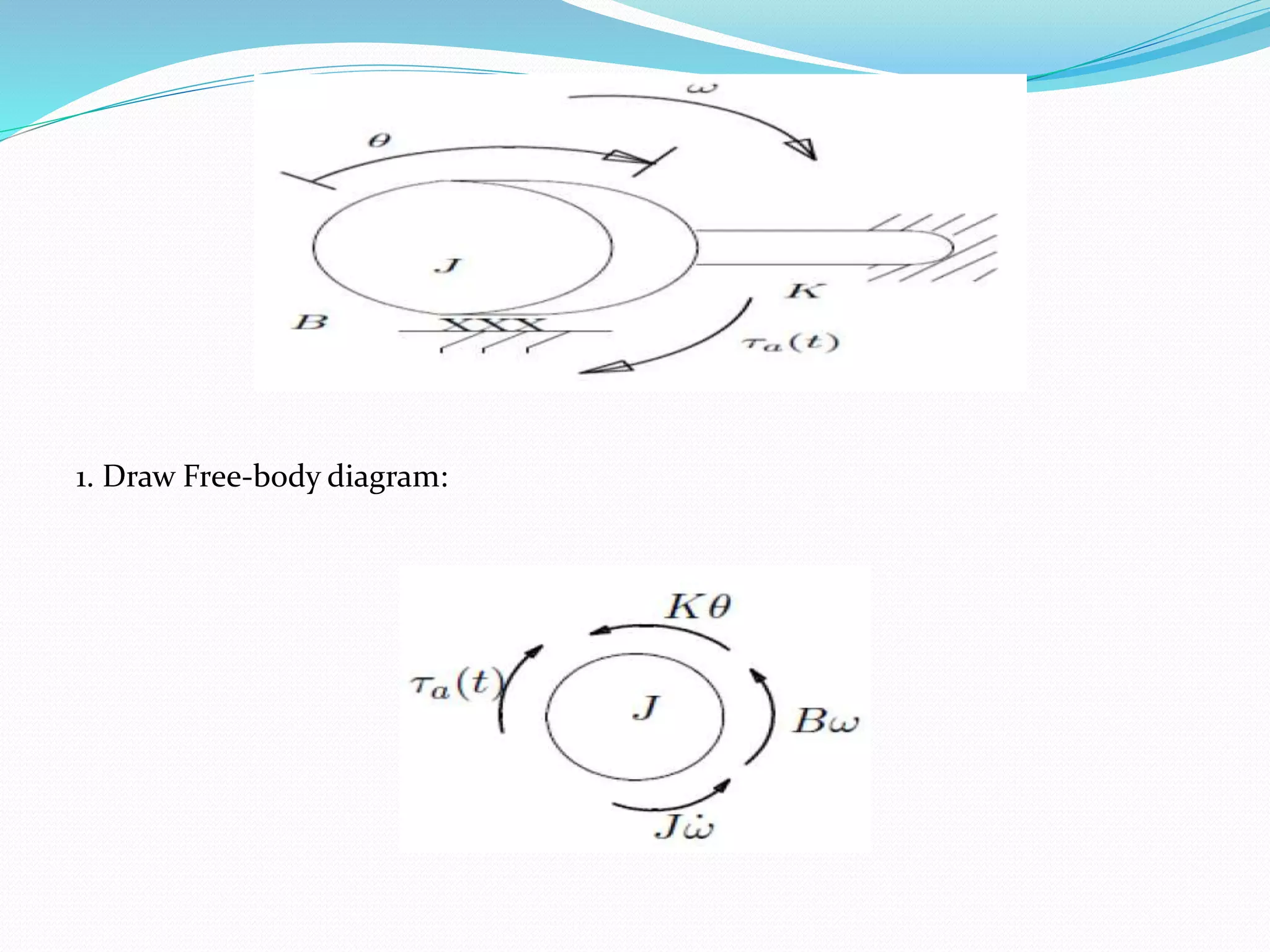
This document discusses translational and rotational mechanical systems. It begins by defining variables for translational systems like displacement, velocity, acceleration, force, work, and power. It then discusses element laws for translational systems including viscous friction and stiffness elements. The document also introduces rotational systems and defines variables like angular displacement, velocity, acceleration, and torque. It discusses element laws for rotational systems including moment of inertia, viscous friction, and rotational stiffness. Finally, it covers interconnection laws for both translational and rotational systems and provides an example of obtaining the system model for a rotational system.

1. PRESENTED BY
Vipin Kumar Maurya
ROLL NO. 1604341510

2. CONTENTS
1. Translational mechanical system
2. Interconnection law
3. Introduction of rotational system
4. Variable of rotational system
5. Element law of rotational system
6. Interconnection law of rotational system
7. Obtaining the system model of Rotational system
8. References

3. TRANSLATIONAL MECHANICAL SYSTEMS
BACKGROUND AND BASICS VARIABLES

4.  x; v; a; f are all functions of time, although time dependence
normally dropped (i.e. we write x instead of x(t) etc.)
 As normal
 Work is a scalar quantity but can be either
 Positive (work is begin done, energy is being dissipated)
 Negative (energy is being supplied)

5.  Generally
 Where f is the force applied and dx is the displacement.
 For constant forces

6. Power
 Power is, roughly, the work done per unit time (hence a scalar
too)
Element Laws
( w(t0) is work done up to t0 )
 The first step in obtaining the model of a system is to write down a
mathematical relationship that governs the Well-known formulae
which have been covered elsewhere.

7. Viscous friction
 Friction, in a variety of forms, is commonly encountered in
mechanical systems. Depending on the nature of the friction
involved, the mathematical model of a friction element may
take a variety of forms. In this course we mainly consider
viscous friction and in this case a friction element is an
element where there are an algebra relationship between the
relative velocities of two bodies and the force exerted.

8. Stiffness elements
 Any mechanical element which undergoes a change in shape
when subjected to a force, can be characterized by a stiffness
element .
Pulleys
 Pulleys are often used in systems because they can change the
direction of motion in a translational system.
 The pulley is a nonlinear element.

9. Interconnection Law
D’Alembert’s Law
 D’Alembert’s Law is essentially a re-statement of Newton’s
2nd Law in a more convenient form. For a constant mass we
have :

10. Law of Reaction forces
 Law of Reaction forces is Newton’s Third Law of motion often
applied to junctions of elements
Law for Displacements

11. Deriving the system model
 Example - Simple mass-spring-damper system.

12. INTRODUCTION OF ROTATIONAL SYSTEM
 A transformation of a coordinate system in which the new
axes have a specified angular displacement from their
original position while the origin remains fixed. This type
of transformation is known as rotation transformation and
this motion is known as rotational motion.

13. VARIABLES OF ROTATIONAL SYSTEM
Symbol Variable Units
θ Angular displacement radian
ω Angular velocity rads-1
α Angular acceleration rads-2
T Torque Newton-metre

14. ELEMENT LAWS OF ROTATIONAL SYSTEM
 There are three element laws of rotational system.
1. Moment of Inertia
2. Viscous friction
3. Rotational Stiffness

15. Moment of Inertia
As per Newton’s Second Law for rotational bodies
 Jω is the angular momentum of body
 is the net torque applied about the fixed axis of
rotation system.
 J is moment of inertia

16. Viscous friction
 viscous friction would be occure when two rotating
bodies are separate by a film of oil (see below), or
when rotational damping elements are employed

17. Rotational Stiffness
 Rotational stiffness is usually associated with a
torsional spring (mainspring of a clock), or with a
relatively thin, flexible shaft

18. Gears
 Ideal gears have
 1. No inertia
 2. No friction
 3. No stored energy
 4. Perfect meshing of teeth

19. Interconnection Laws of Rotational system
 D’Alembert’s Law
 Law of Reaction Torques
 Law of Angular Displacements

20. D’Alembert’s Law
 D’Alembert’s Law for rotational systems is essentially
a re-statement of Newton’s 2nd Law but this time for
rotating bodies. For a constant moment of Inertia we
have
 Where sum of external torques’ acting
on
body.

21. Law of Reaction Torques
 For two bodies rotating about the same axis, any
torque exerted by one element on another is a
accompanied by a reaction torque of equal
magnitude and opposite direction

22. Law of Angular Displacements
 Algebraic sum of angular displacement around any
closed path is equal to zero

23. Obtaining the system model of Rotational system
 Problem Given:
 Input , 𝜏𝑎(t)
 Outputs
 Angular velocity of the disk (ω)
 Counter clock-wise torque exerted by disc on
flexible shaft.
 Derive the state variable model of the system

24. 1. Draw Free-body diagram:

25. 2. Apply D’Alembert’s Law
3. Define state variables
In state-variable form: