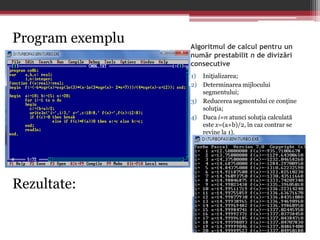
Metoda bisecției este o tehnică numerică utilizată pentru rezolvarea ecuațiilor algebrice și transcendente prin determinarea mijlocului unui interval și reducerea acestuia pe baza semnelor funcției. Algoritmul necesită repetarea calculelor până când intervalul de soluție devine suficient de mic, asigurând o marjă de eroare acceptabilă. Un exemplu de program demonstrează aplicarea acestei metode pentru a găsi soluția unui polinom.

1. Metoda Bisecţiei
Torodii Daria, clasa XII „B”

2. Ce reprezintă metoda bisecţiei?
• Este una din metodele numerice de rezolvare a
ecuaţiilor algebrice şi transcendente.
• Presupune determinarea punctului de mijloc c al
segmentului [a,b], apoi calculul valorii f(c). Dacă
f(c)=0, atunci c este soluţia exactă a ecuaţiei. În
caz contrar, soluţia este căutată pe unul dintre
segmentele [a,c] şi [c,b]. Ea va aparţine
segmentului pe care semnul funcţiei în
extremităţi este diferit.

3. • f(c) – continuă pe segmentul [a,b];
• f(a) × f(b) < 0
Calculul consecutiv al segmentelor care conţin soluţia ecuaţiei
f(x)=0

4. Estimarea erorii
• Deoarece soluţia exactă a ecuaţiei este un punct
al segmentului [ai,bi], rezultă că diferenţa dintre
soluţia exactă şi cea calculată nu depăşeşte
lungimea acestui segment. Prin urmare,
localizarea soluţiei pe un segment cu lungimea ε
asigură o eroare de calcul a soluţiei ce nu
depăşeşte valoarea ε:
|ξ – ci|< ε =|bi – ai|

5. Algoritmul de calcul pentru un
număr prestabilit n de divizări
consecutive
1) Iniţializarea;
2) Determinarea mijlocului
segmentului;
3) Reducerea segmentului ce conţine
soluţia;
4) Daca i=n atunci soluţia calculată
este x=(a+b)/2, în caz contrar se
revine la 1).
Program exemplu
Rezultate:

6. Algoritmul de calcul pentru o
precizie ε dată
1) Determinarea mijlocului segmentului;
2) Reducerea segmentului ce conţine
soluţia;
3) Dacă |b – a|< ε atunci soluţia este
x=(a+b)/2. În caz contrar se revine la
1).
Rezulate
x=3.00000000 f(x):= -2.97998499
x=3.50000000 f(x):= 13.00208663
x=3.25000000 f(x):= 4.33986565
x=3.12500000 f(x):= 0.51785343
x=3.06250000 f(x):= -1.27084722
x=3.09375000 f(x):= -0.38653598
x=3.10937500 f(x):= 0.06313734
x=3.10156250 f(x):= -0.16232822
x=3.10546875 f(x):= -0.04975284
x=3.10742188 f(x):= 0.00665288
x=3.10644531 f(x):= -0.02155982
x=3.10693359 f(x):= -0.00745593
x=3.10717773 f(x):= -0.00040214
x=3.10729980 f(x):= 0.00312521
x=3.10723877 f(x):= 0.00136150
Program exemplu
program cn07;
var a,b,c,eps:real;
function f(x:real):real;
begin f:=x*x*x+2*cos(x)-28; end;
begin a:= 2; b:=4; eps:=0.0001;
repeat
c:=(b+a)/2;
writeln('x=',c:10:8, ' f(x):=', f(c):12:8);
if f(c)=0 then break
else if f(c)*f(a)>0 then a:=c else b:=c;
until abs(b-a)<eps; readln;
end.

7. Exerciţii propuse