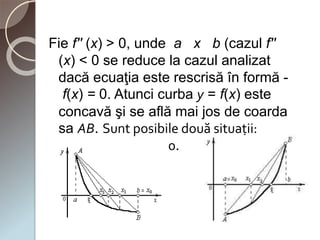
Metoda coardelor este utilizată pentru a găsi rădăcina aproximativă a ecuației f(x)=0 într-un interval [a, b] unde f(a)*f(b) < 0. Această metodă implică iterații pentru a obține convergența către o soluție sau o secvență de intervale, utilizând coordonata punctului de intersecție cu axa absciselor. Funcția f(x) trebuie să fie continuă pe interval și se pot analiza două cazuri în funcție de semnele lui f(a).

1. Metoda coardelor
Autor: Ivanciuc Daniela
Profesor: Josu Larisa

2. Metoda este utilizată pentru găsirea
rădăcinii aproximative  a ecuaţiei
f(x)=0 izolate într-un interval a, b în
cazul în care f(a)*f(b)<0 cu
aproximarea  prestabilită.
Se consideră ecuaţia f(x)=0. Funcţia f(x)
este continuă pe[a, b]. Presupunem că
în urma unui proces de separare a
rădăcinilor ecuaţia f(x)=0 are cel mult o
rădăcină în [a, b].
Prin - notăm rădăcina ecuaţiei pe [a, b].

3. Din ecuaţia coardei
se poate obţine coordonata punctului de intersecţie xi al
coardei cu axa absciselor
După un anumit număr de paşi se obţine, fie o rădăcină
exactă =xi, astfel încît f(xi)=0, fie o secvenţă de intervale
[a0, b0], [a1, b1]… [ai, bi]…
Cu ai+1 = ai , bi+1= xi , dacă f(ai)*f(bi)0
ai+1 = xi , bi+1= bi , dacă f(ai)*f(xi)0.

4. Fie f'' (x) > 0, unde a х b (cazul f''
(x) < 0 se reduce la cazul analizat
dacă ecuaţia este rescrisă în formă -
f(x) = 0. Atunci curba у = f(x) este
concavă şi se află mai jos de coarda
sa АВ. Sunt posibile două situaţii:
f(а) > 0 şi 2) f(a) < 0.

5. În primul caz capătul а al segmentului rămîne
nemişcat, dar iteraţiile consecutive:
x0 = b;
formează un şir mărginit, monoton
descrescător cu proprietate:
În cazul al doilea rămîne nemişcat capătul
b, dar iteraţiile consecutive:
x0 = а;

6. Program
PROCEDURE Coarda(a,b,eps:Real;var xsol:Real);
Var c,d:Real;
BEGIN...
c:=a;
Repeat d:=c;
c:=a-f(a)*(b-a)/(f(b)-f(a));
if f(a)*f(c)<0 then b:=c else a:=c
until Abs(d-c)<eps;
xsol:=c;
end.