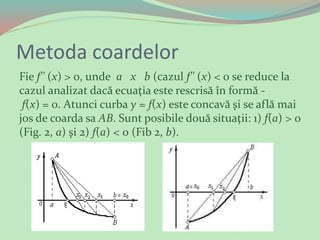
Metoda coardelor este utilizată pentru a determina aproximativ rădăcinile ecuației f(x)=0 în intervalul [a, b] unde f(a) * f(b) < 0. Aceasta implică împărțirea intervalelor anterioare și utilizarea secantei pentru a obține o aproximare a rădăcinii. Metoda poate duce fie la o rădăcină exactă, fie la o succesiune de intervale în care semnele funcției și ale derivatei de ordinul doi se analizează pentru determinarea următoarei aproximații.

1. 24.11.2015

2. Metoda coardelor
1. Metoda este utilizată pentru găsirea rădăcinii
aproximative  a ecuaţiei f(x)=0 izolate într-un
interval a, b în cazul în care f(a)*f(b)<0 cu
aproximarea  prestabilită.
2. Se consideră ecuaţia f(x)=0. Funcţia f(x) este
continuă pe[a, b]. Presupunem că în urma unui
proces de separare a rădăcinilor ecuaţia f(x)=0 are cel
mult o rădăcină în [a, b].
3. Prin - notăm rădăcina ecuaţiei pe [a, b].

3. Metoda coardelor
Intervalele succesive a1, b1, a2, b2 … ai, bi se obţin
prin împărţirea intervalului anterior în raportul
f(ai -1,)/f(bi -1)
Metoda secantei este echivalentă cu înlocuirea f(x), prin
coarda care trece prin punctele (ai, f(ai)) şi (bi, f(bi))

4. Metoda coardelor
Din ecuaţia coardei
se poate obţine coordonata punctului de intersecţie xi al coardei cu axa
absciselor
După un anumit număr de paşi se obţine, fie o rădăcină exactă =xi, astfel
încît f(xi)=0, fie o secvenţă de intervale
[a0, b0], [a1, b1]… [ai, bi]…
Cu ai+1 = ai , bi+1= xi , dacă f(ai)*f(bi)0
ai+1 = xi , bi+1= bi , dacă f(ai)*f(xi)0.

5. Metoda coardelor
Fie f'' (x) > 0, unde a х b (cazul f'' (x) < 0 se reduce la
cazul analizat dacă ecuaţia este rescrisă în formă -
f(x) = 0. Atunci curba у = f(x) este concavă şi se află mai
jos de coarda sa АВ. Sunt posibile două situaţii: 1) f(а) > 0
(Fig. 2, а) şi 2) f(a) < 0 (Fib 2, b).

6. Metoda coardelor
În primul caz capătul а al segmentului rămîne nemişcat, dar
iteraţiile consecutive:
x0 = b;
formează un şir mărginit, monoton descrescător cu
proprietate:
În cazul al doilea rămîne nemişcat capătul b, dar iteraţiile
consecutive:
x0 = а;
(2)

7. Generalizînd, conchidem:
1. Nemişcat este acel capăt al intervalului pentru care
semnul funcţiei f (х) coincide cu semnul derivatei de
ordinul doi f'' (х);
2. Aproximări consecutive xn se află în acea parte de
rădăcină  unde funcţia f (х) are semnul opus
semnului derivatei de ordinul doi f'' (х).

8. Exerciții
Determinaţi soluţiile ecuaţiilor, utilizând metoda
coardelor: