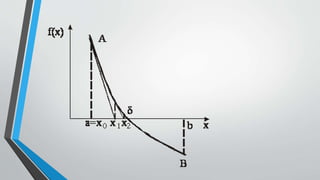
Metoda Newton este utilizată pentru găsirea radacinilor reale ale unei ecuații, presupunând continuitatea derivatelor pe intervalul [a, b]. Formula iterativă Newton este xk+1 = xk - f(xk)/f'(xk), cu un punct de start x0 ales din a, asigurând condiția f'(x0)*f''(x0) > 0. Această metodă converge mai repede decât metoda aproximatiilor succesive, dar necesită evaluarea funcției și a derivatelor, ceea ce poate fi problematic în cazul funcțiilor tabelate.

1. Metoda Newton

2. Fie ecuatia f(x) = 0, algebrica sau transcendenta, care are
o singura radacina reala in intervalul [a, b]. Se presupune
ca derivatele f'(x) si f''(x) sunt continue si pastreaza
acelasi semn pe intervalul [a, b].

4. Intr-un punctAk(Xk,f(xk)) , ecuatia tangentei la curba y = f(x) este f(x)- f(xk)=f'(Xk)(X-Xk)
Punctul de intersectie a tangentei cu axa Ox este xk+1 (pentru f(x) = 0 si x = xk+1):
Xk+1=Xk-f(Xk)/f'(Xk) , k = 0,1,.care este formula iterativa Newton.
Punctul de start x0 trebuie sa fie chiar a, astfel incat f'(X0)*f''(X0)>O si X1 apartine [a,b}.

5. Observatie:
Metoda tangentelor converge mai rapid decat metoda aproximatiilor
succesive dar necesita evaluarea functiei si a derivatelor sale, la fiecare pas,
lucru care poate fi dificil sau chiar imposibil daca functia nu este cunoscuta
analitic ci tabelata.

6. Va multumesc pentru atentie !!
Viznovici Alina ,
cl. a XII-a "B"