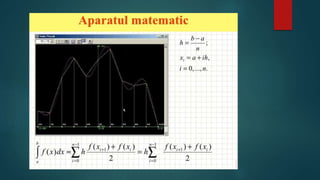
Documentul discută integrarea numerică integrală în analiza matematică, subliniind importanța integralei ca generalizare a conceptelor de arie, masă, volum și sumă. Se explică diferitele metode de integrare, cum ar fi metoda dreptunghiurilor și metoda trapezelor, focuse pe eficiența acestora în determinarea ariei figurilor curbilinii. Detaliile tehnice sunt prezentate, inclusiv modul în care trapezul este utilizat pentru aproximarea ariei pe segmentele elementare.

1. Integrarea
numerica

2. Integrala
 În analiza matematică, integrala unei funcții este o generalizare a
noțiunilor de arie, masă, volum și sumă. Procesul de determinare a
unei integrale se numește integrare. Spre deosebire de noțiunea
înrudită de derivată, există mai multe definiții posibile ale integralei,
fiecare cu suportul său tehnic. Acestea sunt însă compatibile.
Oricare două moduri de integrare a unei funcții vor da aceleași
rezultate când ambele sunt definite.

3. Metoda dreptunghiurilor
 Determinarea ariei unei figuri curbilinii este destul de
dificilă, de aceea se utilizează procedura de
aproximare a figurii iniţiale prin un set de figuri
geometrice, ariile cărora se determină după formule
standard

5. Metoda trapezelor
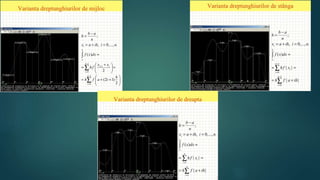
 Metoda trapezelor A proximare a a riei unui trapez curbiliniu este
mult mai eficientă în cazul cînd pe fiecare din segmentele
elementare este aproximată prin un trapez, şi nu prin dreptunghi. Pe
segmentul elementar [x i , x i+1 ] trapezul este determinat de
extremităţile segmentului pe axa 0X ( x i ,0 ) ( x i+1 0 ) şi de valoarea
funcţiei f(x) în extremităţi: ( x i ,f(x i ) ) ( x i+1 , f(x i+1 ) )

7. Va multumesc pentru atentie !!!
Viznovici Alina
cl. a XII-a "B"