Metoda reluării este o tehnică de căutare a soluției prin explorarea stărilor posibile, prezentată printr-o schemă recursivă. Aceasta prezintă o complexitate algoritmică crescută comparativ cu metoda trierii, dar este capabilă să rezolve probleme analogice. Exemple de probleme rezolvate includ selectarea numerelor din mulțimi pentru a atinge o sumă specificată și generarea submulțimilor de litere dintr-un alfabet.

1. T O R O D I I D A R I A , C L A S A X I B
Metoda Reluării

2. M E T O D A R E L U Ă R I I – P R E S U P U N E C Ă S O L U Ţ I A
P R O B L E M E I P E C A R E T R E B U I E S Ă O R E Z O L V Ă M
P O A T E F I R E P R E Z E N T A T Ă P R I N T R - U N V E C T O R :
X=(X1, X2, …, XK , …, XN ).
F I E C A R E C O M P O N E N T Ă A V E C T O R U L U I X P O A T E
L U A V A L O R I D I N T R - O A N U M I T Ă M U L Ţ I M E A K . S E
C O N S I D E R Ă C Ă E L E M E N T E L E M U L Ţ I M I I A K S U N T
O R D O N A T E C O N F O R M U N U I C R I T E R I U B I N E
S T A B I L I T .
Ce reprezintă metoda reluării ?

3. Căutarea soluţiei prin metoda
reluării
G
E
N
E
R
A
L
I
T
Ă
Ţ
I

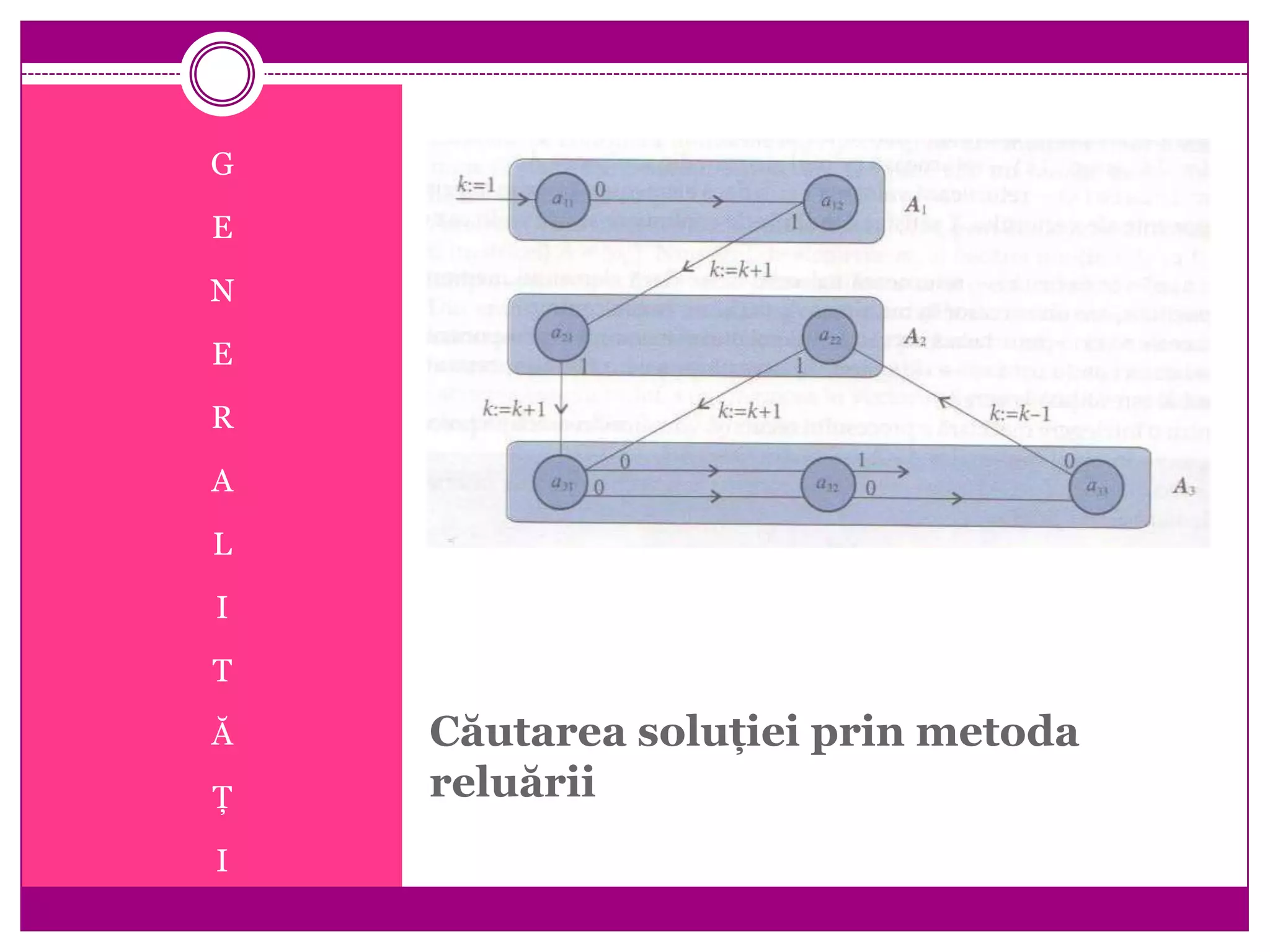
4. Schema generală
Procedure Reluare (k:integer);
Begin
if k<=n then begin
X[k]:=PrimulElement(k);
if Continuare(k) then Reluare(k+1);
while ExistaSuccesor(k) do
Begin
X[k]:=Succesor(k);
if Continuare(k) then Reluare(k+1)
end;
end
else PrelucrareaSolutiei;
End;

5. Metoda Trierii Metoda Reluării
 Complexitatea
algoritmului: O( )
 Timpul cerut de
algoritmul respectiv
este foarte mare;
 Soluţionează aceleaşi
probleme
 Complexitatea
algoritmului: O( )
 Timpul cerut de
algoritmul respectiv
este mai mic;
 Soluţionează aceleaşi
probleme
Diferenţa dintre metodele trierii şi reluării

6. Exemple de probleme
 Se consideră mulţimile A1, A2, …, An fiecare mulţime
fiind formată din mk numere naturale. Selectaţi din
fiecare mulţime cîte un număr în aşa mod încît suma
lor să fie egală cu q.
 Se consideră mulţimea B={b1, b2, …, bn} formată în
primele n litere ale alfabetului latin. Elaboraţi un
program care generează toate submulţimile Bi
formate exact din q litere.
 Elaboraţi un program care afişează la ecran toate
modurile de a descompune un număr natural în
sumă de k numere naturale distincte.

7. H T T P : / / I N F O . M C I P . R O / ? T = B A C K
H T T P : / / S O F T W A R E . U C V . R O / ~ C S T O I C A / T P / B A
C K T R A C K I N G . P D F
Link-uri utile