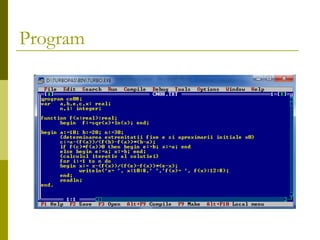
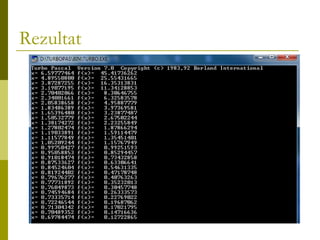
Metoda coardelor este utilizată pentru găsirea aproximativă a rădăcinilor ecuațiilor f(x)=0, în special când soluțiile nu pot fi obținute analitic. Această metodă implică împărțirea unui interval [a, b] și generarea de noi intervale prin evaluarea funcției la capetele intervalelor. Documentul discută cum să se aplice această metodă la ecuația f(x) = sqr(x) + ln(x) pe intervalul [10, 20] pentru 30 de iterații.

1. Metoda coardelor
Balan Veronica, a XII-a “B”

2. Ce reprezintă?
 Metoda coardelor este metoda utilizată
pentru găsirea rădăcinii aproximative x a
ecuaţiei f(x)=0 izolate într-un interval
[a, b] în cazul în care f(a)*f(b)<0 cu
aproximarea e prestabilită.

3. Cînd se utilizează?
 Metoda coardelor se folosește la rezolvarea
ecuațiilor algebrice și transcendente, soluțiile
cărora nu pot fi găsite analitic.
Se consideră ecuația f(x)=0.
 Presupunem că în urma unui proces de separare
a rădăcinilor ecuaţia f(x)=0 are cel mult o
rădăcină în [a, b].
Prin x- notăm rădăcina ecuaţiei pe [a, b].
 Intervalele succesive [a1, b1], [a2, b2] … [ai, bi] se
obţin prin împărţirea intervalului anterior în
raportul f(ai-1)/f(bi-1)

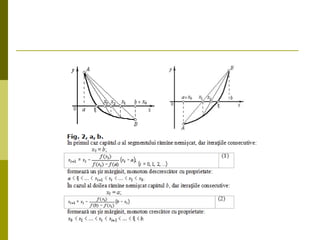
4.  Metoda coardelor este echivalentă cu înlocuirea
f(x), prin coarda care trece prin punctele (ai,
f(ai)) şi (bi, f(bi))
Din ecuaţia coardei x -
a
y -
f ( a
)
 i
=
i
b -
a
f ( b ) -
f ( a
)
se poate obţine
coordonata punctului i de i
intersecţie i i
xi al coardei
cu axa absciselor
x = a f b -
b f a
( ) ( )
i i
i i i i
i f b -
f a
( ) ( )
y
f(bi)
f(ai)
x
i
ai x bi
x
 După un anumit număr de paşi se obţine, fie o
rădăcină exactă x=xi, astfel încît f(xi)=0, fie o
secvenţă de intervale[a0, b0], [a1, b1]… [ai, bi]…
Cu ai+1 = ai , bi+1= xi , dacă f(ai)*f(bi)<0
ai+1 = xi , bi+1= bi , dacă f(ai)*f(xi)>0.

5.  Fie f'' (x) > 0, unde a < х < b (cazul
f'‘(x) < 0 se reduce la cazul analizat dacă
ecuaţia este rescrisă în formă - f(x) = 0).
Atunci curba у = f(x) este concavă şi se află
mai jos de coarda sa АВ.
 Sunt posibile două situaţii:
1) f(а) > 0 (Fig. 2, а) şi 2) f(a) < 0 (Fib 2, b).

7. Generalizînd, conchidem:
 Nemişcat este acel capăt al intervalului pentru
care semnul funcţiei f (х) coincide cu semnul
derivatei de ordinul doi f'' (х);
 Aproximări consecutive xn se află în acea parte
de rădăcină x unde funcţia f (х) are semnul opus
semnului derivatei de ordinul doi f'' (х).
 Pentru oprire a procesului iterativ putem folosi
sau condiţia ½ f(xn)½< e , sau condiţia
½xn – xn - 1½<e., unde e - eroare absolută iniţial
dată.

8. Problemă
 Determină solu țiile ecuației,utilizînd
metoda coardelor
F(x)= sqr(x)+ln(x)
pe [10,20] pentru 30 de iterații

9. Program

10. Rezultat