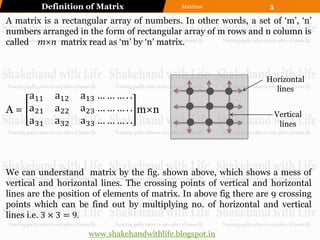
The order of the given matrix is 2×3. So the maximum no. of elements is 2×3 = 6.
The correct option is B.
The element a32 belongs to 3rd row and 2nd column.
The correct option is B.
3. A matrix whose each diagonal element is unity and all other elements are zero is called
A) Identity matrix B) Unit matrix C) Scalar matrix D) Diagonal matrix
4. A matrix whose each row sums to unity is called
A) Row matrix B) Column matrix C) Unit matrix D) Stochastic matrix
5. The sum of all the elements on the principal diagonal of a square