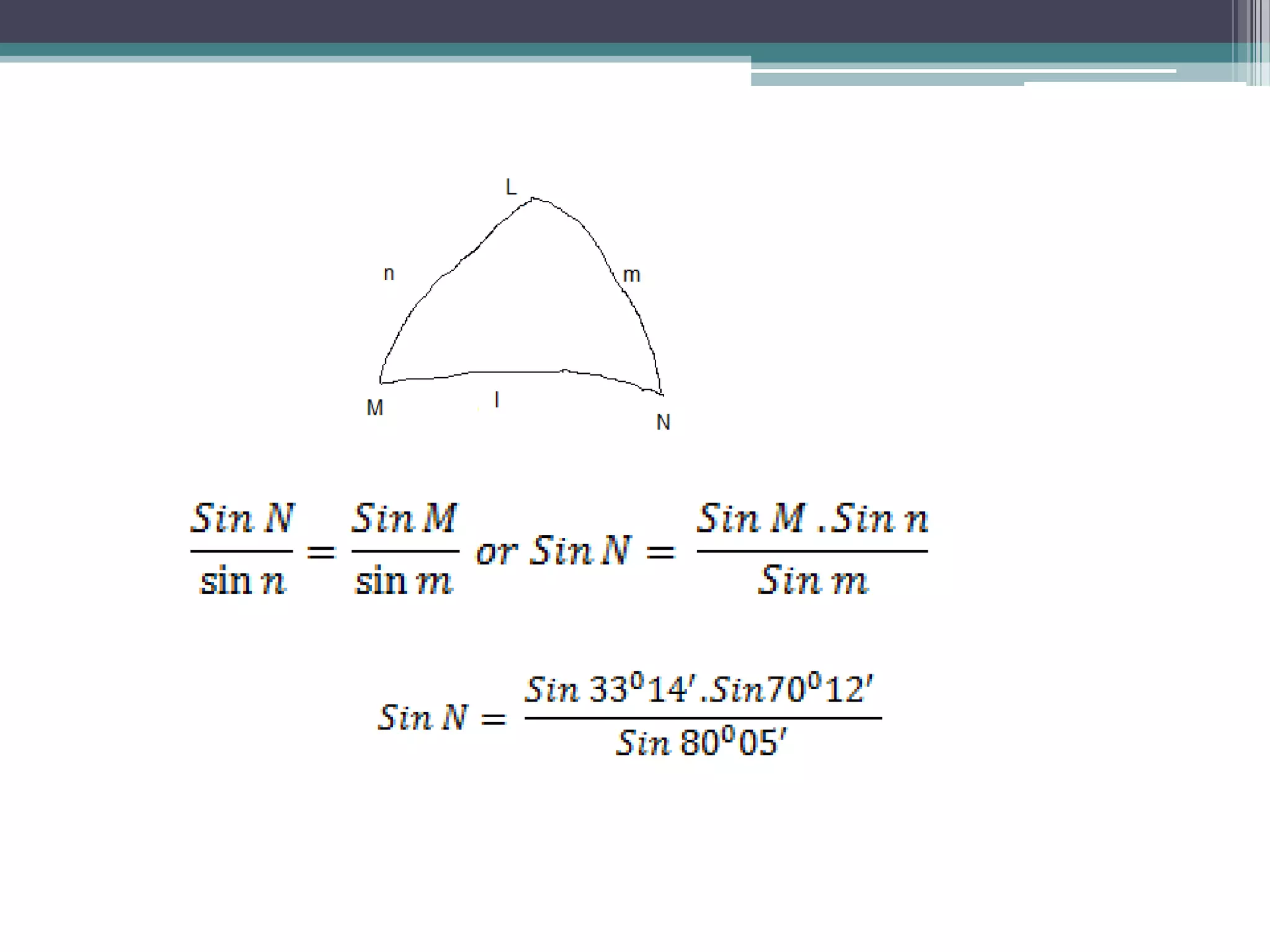
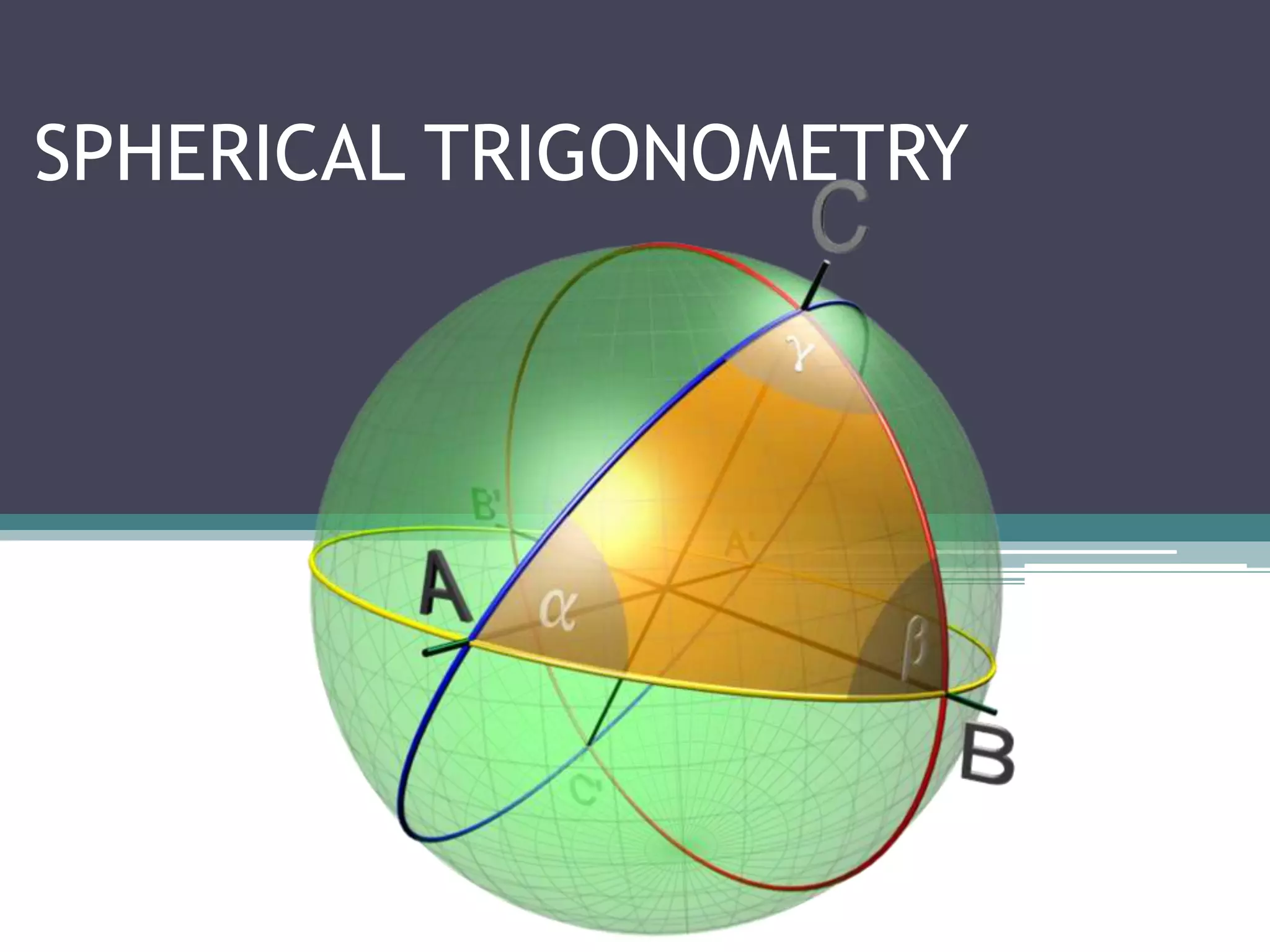
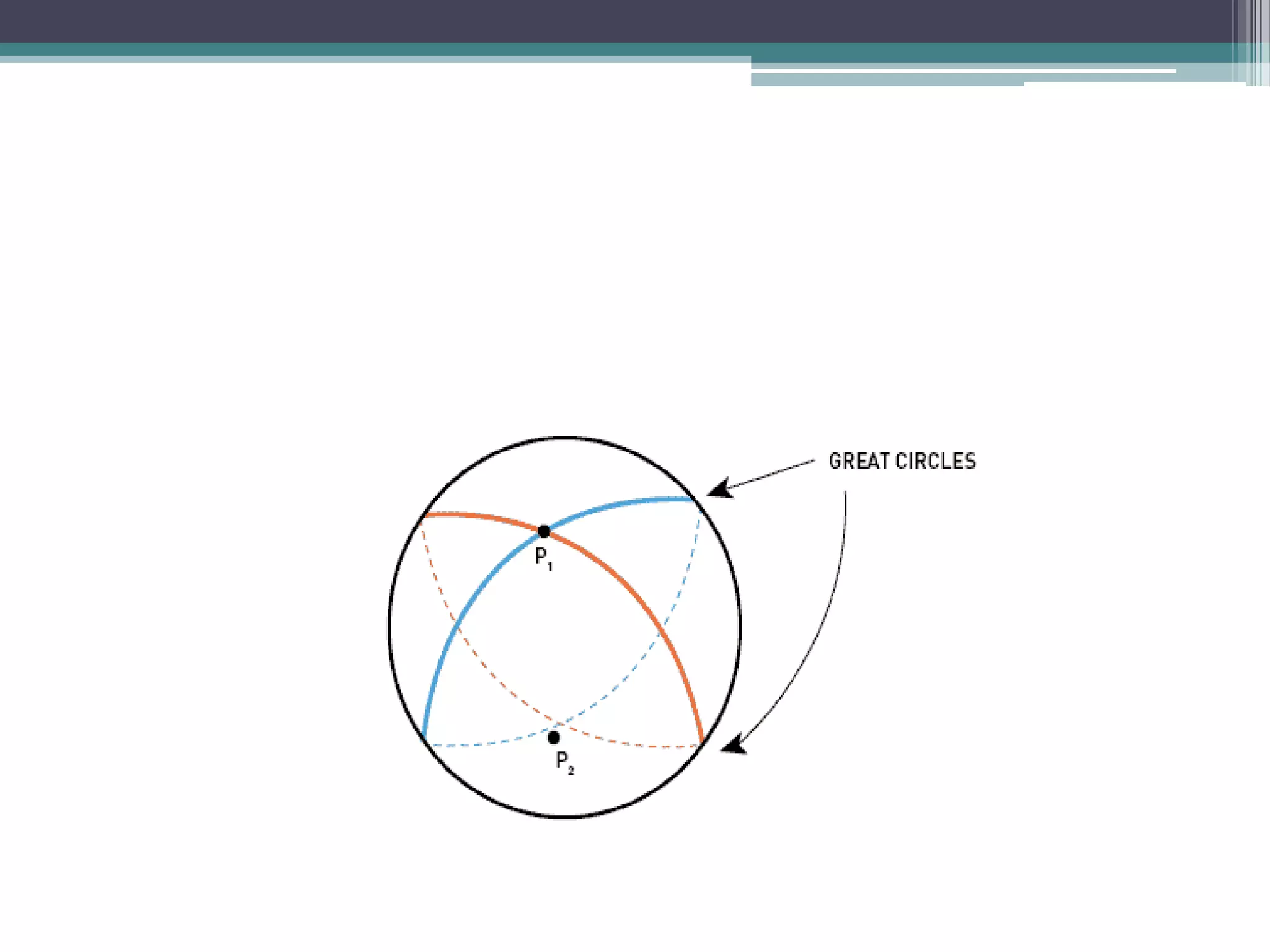
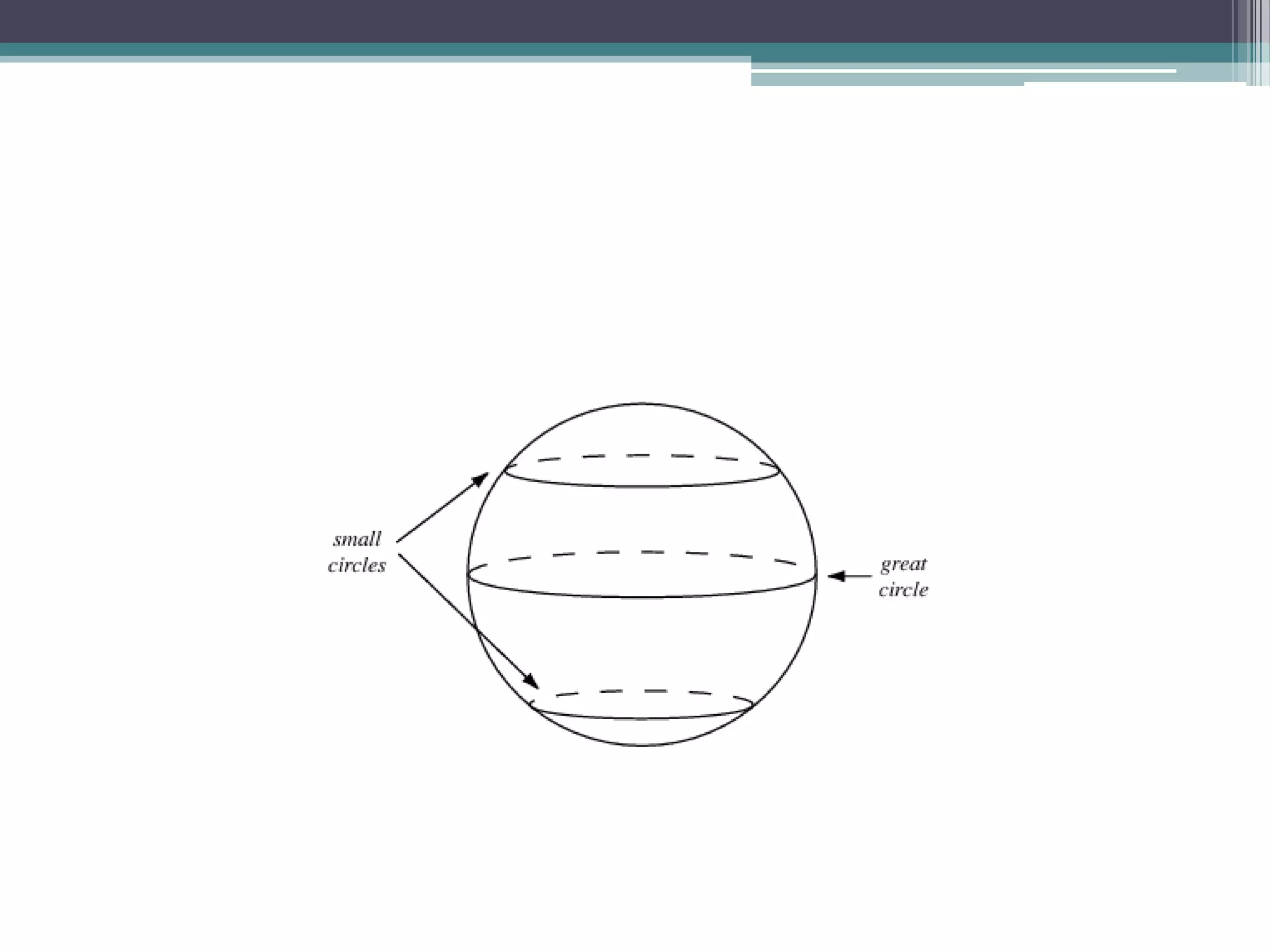
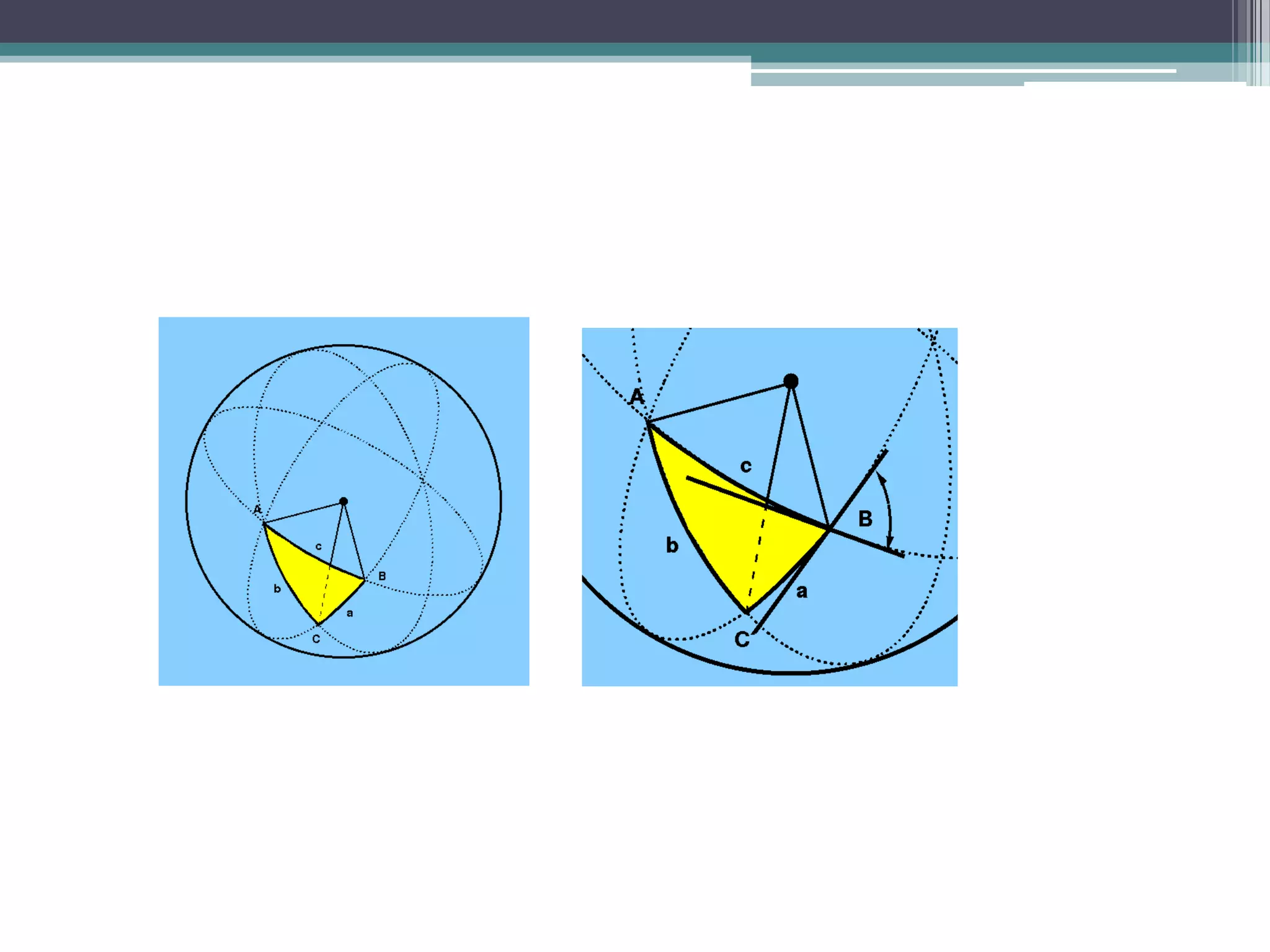
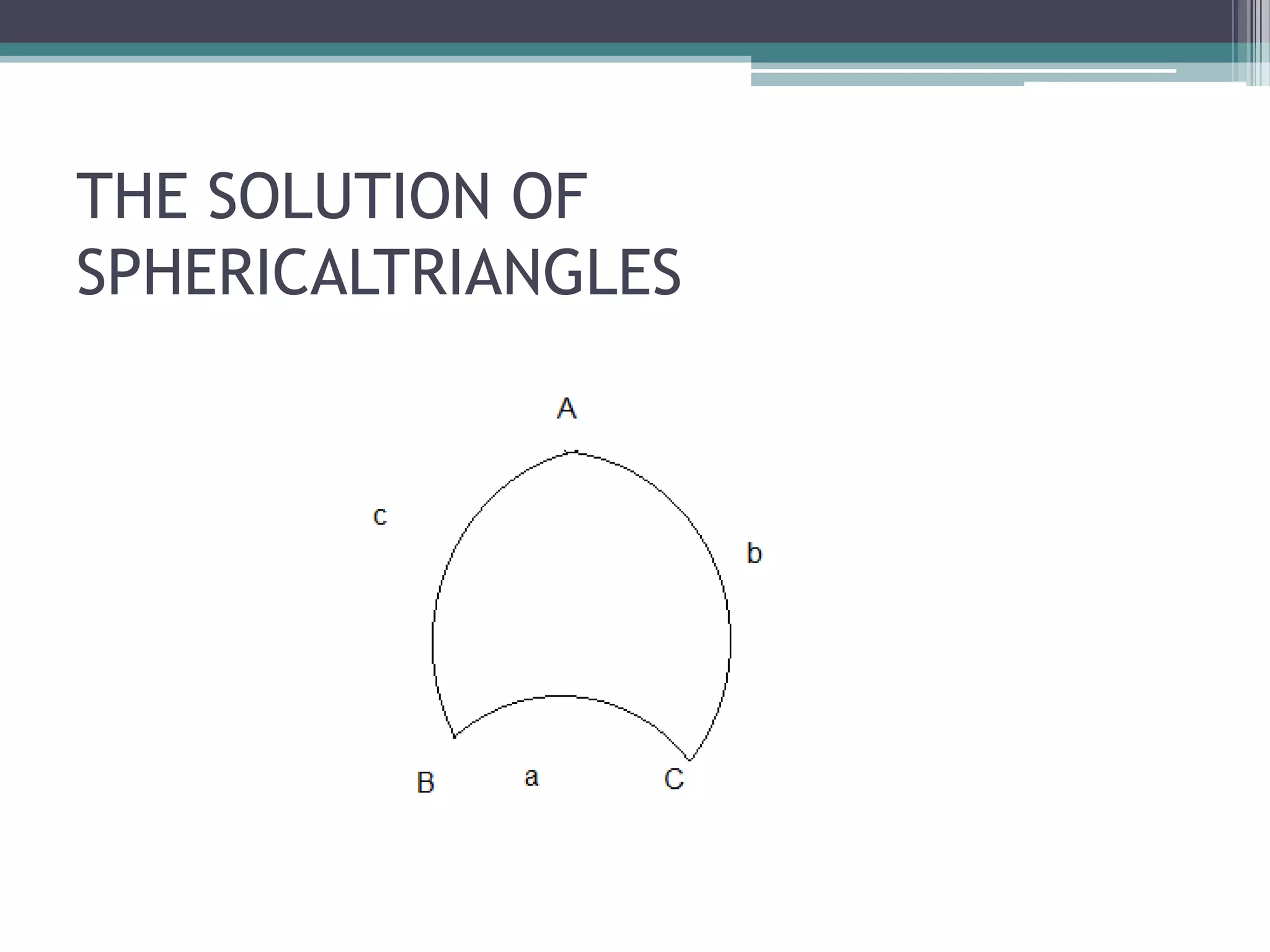
This document provides information on spherical trigonometry. It defines key terms like great circles, small circles, spherical angles, and spherical triangles. It describes properties of these concepts, such as every great circle passing through the center of a sphere. Formulas for solving spherical triangles are presented, including the Sine Formula, Cosine Formula, and Haversine Formula. Examples show how to use these formulas to calculate unknown sides and angles of spherical triangles given other information.

1. SPHERICAL TRIGONOMETRY

2. 1. SPHERICAL TRIGONOMETRY
FUNDAMENTALS

3. GREAT CIRCLE
• A great circle is a circle, on the SURFACE OF A
sphere, whose plane passes through the centre of
the sphere.

5. Note:
(a) A great circle divides the sphere into two identical
parts, each called hemisphere.
(b) The radius of a great circle is equal to that of the sphere.
(c) Any number of great circles could pass through a given
point on the surface of the sphere. However, all these
great circles would also pass through a point
diametrically opposite to the given point.
(d) Only one great circle can pass through any two given
points on the surface of a sphere. However if the two
points are diametrically opposite to each other, any
number of great circles can pass through the two
points.

6. POLES OF A GREAT CIRCLE
The pole of a great circle is a point, on the
surface of the sphere, which is equidistant, and
hence ninety degrees away from, all parts of the
circumference of the great circle each great circle
would, therefore, have two poles which are
situated diametrically opposite to each other.

7. Small circle
• A small circle is a circle, on the surface of a
sphere, whose plane does not pass through the
centre of the sphere.
• Note:
the radius of a small circle is less than that of
the sphere

9. SPHERICAL ANGLE
• A spherical angle is an angle, on the surface of a
sphere, formed by the intersection of two great
circles.

10. NOTE:
(a) In practice, a spherical angle can be measured
by drawing tangents to the two great circle arcs
from the point of intersection. The value of the
angle between the tangents is the magnitude of
the spherical angle.
(b) The maximum value of a spherical angle is two
right angles(180 degrees).
(c) Vertically opposite angles are equal.

11. SPHERICAL TRIANGLE
• A spherical triangle is a triangle on the surface of
a sphere, formed by the intersection of three
great circles.

13. PROPERTIES OF SPHERICAL TRIANGLES
(a) The magnitude of the side of a spherical
triangle is the angle subtended by it at the centre
of the sphere and is expressed in degrees and
minutes of arc.
(b) The maximum value of a side of a spherical
triangle is 1800.
(c) The maximum value of an angle of a spherical
triangle is 1800.
(d) The sum of the three sides of a spherical
triangle is less than 3600.

14. (e) The sum of the three angles of a spherical triangle
is any value between two right angle s and six right
angles.(i.e., between 1800 and 5400).
(f) The sum of any two sides of a spherical triangle is
greater than the third.
(g) The greater side has the greater angle opposite to
it.
(h) If two sides of a spherical triangle are equal, the
angles opposite to them are also equal to each other.

15. (i) A RIGHT ANGLED spherical triangle is one
in which an angle equals to 900. in a spherical
triangle, it is possible for more than one angle
to be equal to 900.
(j) A QUADRANTAL spherical triangle is one in
which one side equals to 900 .In a spherical
triangle, it is possible for more than one side to
be equal to 900.

16. (k) A spherical triangle which is not a right angled
or a quadrantal one is called an OBLIQUE
spherical triangle.

17. SYMMETRICAL SPHERICAL TRIANGLES
• Two spherical triangles are said to be symmetrically
equal when each of the six elements (i.e., three sides
and three angles) of one are equal in value to each of
the six elements of the other.
• Because spherical triangles lie on the surface of a
sphere, and are hence three
dimensional, ‘symmetrically equal’ does not
necessarily mean congruent. Two triangles are said
to be congruent only if it is possible to superimpose
one on the other.

18. • In the following figure, ABC and DEF are two
spherical triangles as seen from OUTSIDE the
sphere. All six elements of triangle ABC are
correspondingly equal to the six elements of
triangle DEF. however the triangles are latterly
inverted(are mirror images) and, both being
convex, it is not possible to superimpose one on
the other. The two triangles
are, therefore, symmetrically equal but not
congruent.

19. Ω
Ω

20. Two spherical triangles are
symmetrically equal if;
(a) Three sides of one are correspondingly equal to
the three sides of the other
(b) Two sides and the included angle of one are
respectively equal to the two sides and included
angle of the other.
(c) Three angles of one are respectively equal to the
three angles of the other
(d) Two angles and the included side of one are
respectively equal to the two angles and
included side of the other.

21. THE SOLUTION OF
SPHERICALTRIANGLES

22. Sin Formula

23. Cosine formula
(if three sides are known)

24. Where two sides and the included angle are known, the
foregoing cosine formula may be rearranged as follows.

25. • Whereas the value of cosine is positive in the
first quadrant and negative in the second
quadrant, the value of sine is positive in
both, the first and the second quadrants.
• Ex:
If cos A = 0.5, A = 600.
But if sin A = 0.5, A = 300 or 1500

26. • To avoid such ambiguities in navigation, the
Haversine formula was invented.

27. • Haversine of an angle increases as the angle
increases from 0 degrees to 180 degrees, without
any change of sign. The magnitude of the angles
and sides of a spherical triangle cannot exceed
180 degrees, the possibility of ambiguity is
eliminated by using the haversine formula.
• Ex: Hav 300 = 0.06699 and Hav 1500 = 0.93301

28. THE HAVERSINE FORMULA
The haversine formula may be applied in:1. The general format
2. The specific format
3. The modified format

29. (1) THE GENERAL FORMAT
Where three sides are known:
HAV one ANGLE = [COSEC one ADJ side].
[COSEC other ADJ side].
[HAV OPP side – HAV DIFF between ADJ sides]

30. • Where 2 sides & included angle are known:
HAV OPP side = [SIN one ADJ side. SIN other
ADJ side.HAV included ANGLE]+HAV diff
between ADJ sides.

31. (2) THE SPECIFIC FORMAT:

32. If a, b and c are known,
• Hav A = cosec b. cosec c [Hav a – Hav (b~c)]
• Hav B = cosec a. cosec c [Hav b – Hav (a~c)]
• Hav C = cosec a. cosec b [Hav c – Hav (a~b)]
If 2 sides and included angle are known:• Hav a = [sin b. sin c. Hav A] + Hav (b~c)
• Hav b = [sin a. sin c. Hav B]+ Hav (a~c)
• Hav c = [sin a. sin b. Hav C]+ Hav (a~b)

33. (3) THE MODIFIED FORMAT:
The LONG by CHRON formula:
Hav LHA = Sec L. Sec D [Hav ZD – Hav (L~D)
The INTERCEPT formula:
Hav CZD = (Hav LHA .Cos L.Cos D) + Hav (L~D)

34. Note:
It is suggested that the Haversine formulae in their
general form be ‘conned by rote’(learned by heart)
as they may then be applied with ease whenever
necessary in solving problems in spherical
trigonometry. The specific format may prove
difficult when the letters denoting the various
elements vary from problem to problem. The
modified formulae are mentioned here for
information only. They are derived from the general
format to suit specific calculations in navigation and
are not part of general spherical trigonometry.
The Haversine formula is derived from the cosine
formula

35. SIMPLE SOLUTIONS
Example 1:
• In spherical triangle PQR, p = 620 10.1’, q =
111035.2’, r = 630 33’. Calculate P.

36. • HAV one ANGLE =[COSEC one ADJ side].[HAV
OPP side – HAV DIFF between ADJ sides]
• Hav P = Cosec q Cosec r [Hav p – Hav (q~r)]

37. Nat Hav p = Hav 620 10.1’ … = 0.26656
Hav (q~r) = Hav (480 02.2’)… = 0.16567 –
Nat Hav P
= 0.10089
Log Hav
Log Cosec q
Log Cosec r
Log Hav P
P = 400 44.7’
= -1 + 0.00386
= 0.03157 +
= 0.04802
= -1 + 0.08345

38. Example 2:
• In spherical triangle WXY, W = 88024.5’, x = 980
10’, y = 1000 09’. Find w and X.

39. HAV OPP side = [SIN one ADJ side.SIN other
ADJ side. HAV included ANGLE] + HAV diff
between ADJ sides.
Hav w = [Sin x . Sin y . Hav W] + Hav (x~y)
Log Sin x(i.e 980 10’)……….= -1+0.99557
Log Sin y(i.e 1000 09’)…… = -1+0.99557
Log Hav W(i.e 880 24.5’)… = -1+0.68674

40. Log Hav ………………………=-1 + 0.67546
Nat Hav ……………………… = 0.47365
Hav (x~y)(i.e 1059’)…………. = 0.00030+
Nat Hav w ……………………. = 0.47395
w = 87001’

41. • To find X:
HAV one ANGLE = [COSEC one ADJ
side].[COSEC other ADJ side – HAV DIFF
between ADJ sides]
Hav X = Cosec w . Cosec y[Hav x – Hav(w~y)]

42. • Nat Hav x = Hav 98010.0’ …………… = 0.57103
• Hav (w~y) = Hav 13008.0’………….=0.01308
• Nat Hav ………………………………=0.55795
•
•
•
•
Log Hav ……………………………=-1+0.74661
Log Cosec w ………………………= 0.00059+
Log Cosec y ……………………….= 0.00685
Log Hav X …………………………= -1 + 0.75405
P = 40044.7’

43. Note:
• X could have, if desired been calculated by the
Sine formula as follows:-
• Log Sin W(i.e. 88024.5’)… = -1+0.99983
• Log Sin x(i.e. 98010’)…. = -1 + 0.99557 +
-1 + 0.99540
Log Sin w(i.e. 87001’)…..….= -1+ 0.99940 Log Sin X ……………………….= -1 + 0.99600
X= 82014’ or 97046’

44. Solution of above Ambiguity
• The greater side must have the greater angle
opposite to it.
• Opposite side
opposite angle
w = 87001’
W = 88024.5’
x = 98010’
X> 88024.5’
Hence X = 97046’ Not 82014’

45. Example 3:
• In spherical triangle LMN, M = 33014.0’, m=800
05’, n = 70012’. Calculate N.
• Since in this problem,
i. Three sides have not been given and
ii. Two sides and the included angle have not
been given,
The Haversine formula (and hence the Cosine
formula) cannot be applied. The sine formula
can, however be used.

47. • Log Sin 88024.5’)… = -1+0.99983
• Log Sin x(i.e. 98010’)…. = -1 + 0.99557 +
-1 + 0.99540
Log Sin w(i.e. 87001’)…..….= -1+ 0.99940 Log Sin X ……………………….= -1 + 0.99600