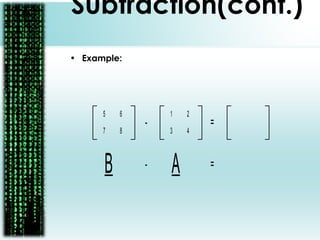
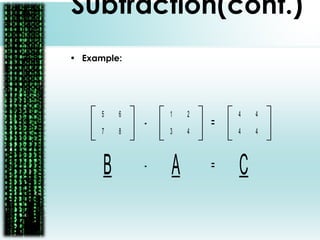
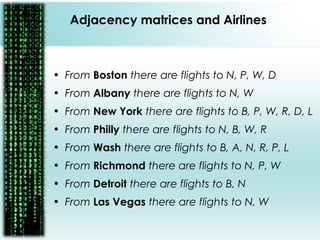
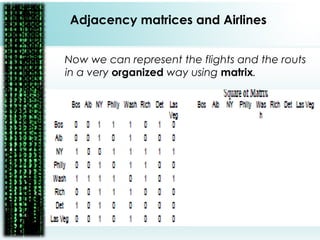
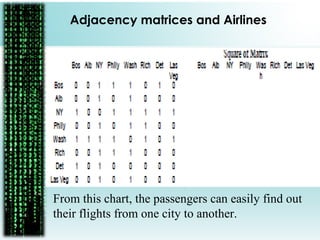
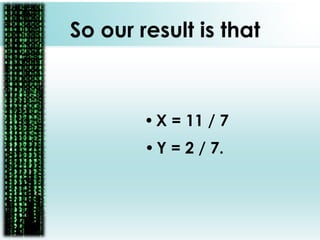The document provides a comprehensive overview of matrices, including their definitions, types (such as square, row, column, diagonal, and unit matrices), and operations like addition, subtraction, multiplication, and inversion. It also highlights the applications of matrices in solving simultaneous equations and their relevance in business contexts, particularly in organizing flight information using adjacency matrices. Overall, it emphasizes the importance of matrix algebra for efficient calculations and business predictions.

2. LET’S START

3. WHAT IS MATRIX?
• > Rectangular presentation of symbols or
numerical elements
• > Arranged systematically in rows and
columns
• >Describes various aspects of a
phenomenon which are inter-related in
some manner.

4. These are some numbers.
1
4
2
3
Numbers can be organized in boxes, e.g.
1
4
2
3

5. Let’s take an example
• We may consider two linier
equations,
2x - 3y + z = 7……. (1)
4x + 5y - 3z = 5…… (2)

6. • Co-efficient of x, y, z in the equations-
In case of (1) are, 2, -3, 1
In case of (2) are, 4, 5, -3

7. So,
(1)and (2) form this matrix
Co-efficient matrix ,
2 x 3 matrix.
(2 rows and 3 columns Matrix)






−
−
354
132

8. •After enclosing by two
brackets, the rectangular
array as well as the Matrix is
treated as a single entry.

9. [ ]
Many Unorganized Numbers
28 39 57 17 38 18 38 65 10 73 16 73 77 63 18 56 18
74 82 20 10 75 84 19 47 14 11 84 08 47 57 58 49 48
88 84 47 48 43 05 61 75 98 47 32 98 15 49 01 38 65
43 17 65 21 79 43 17 59 41 37 59 43 17 97 65 41 35
75 49 03 86 93 41 76 73 19 57 75 49 27 59 34 27 59
43 19 74 32 17 43 92 65 94 13 75 93 41 65 99 13 47
75 83 47 48 73 98 47 39 28 17 49 03 63 91 40 35 42
31 87 49 75 48 91 37 59 13 48 75 94 13 75 45 43 54
75 48 90 37 59 37 59 43 75 90 33 57 75 89 43 67 74
34 92 76 90 34 17 34 82 75 98 34 27 69 31 75 93 45
13 59 84 76 59 13 47 69 43 17 91 34 75 93 41 75 90
34 15 74 91 35 79 57 42 39 57 49 02 35 74 23 57 75
Now it is a Matrix.

10. MATRIX DEFINED
• A matrix is a rectangular array of numbers
arranged in rows and columns enclosed by a pair
of brackets and subject to certain rules of
presentation.
• A matrix can be enclosed by [ ] or || ||
Like,
Or,





−
−
354
132
354
132
−
−

11. EXPRESSING MATRIX
• Matrix is denoted by a capital letter
• Elements are corresponded by small letters
• Small letters are followed by two suffixes m& n
• m represents the order of the Row
• n represents the order of the Column

12. Expressing Matrix (Cont.)
Example,
• A matrix having m rows and n columns
can be written as
nmmnmjmm
inijii
nj
nj
aaaa
aaaa
aaaa
aaaa
A
×














=
21
21
222221
111211

13. TYPES OF MATRIX

14. Square Matrix
• A matrix, in which the number
of rows is equal to the number
of columns, is called a square
matrix.

15. Square Matrix(cont.)
Example:
m x n matrix where m=n ;
(m =row, n = column)
.
21
21
222221
111211
nmmnmjmm
inijii
nj
nj
aaaa
aaaa
aaaa
aaaa
×















16. Row Matrix
• A matrix having a single row is
called a row matrix.
Example:
[a…b…c…d]

17. Column Matrix
• A matrix having a single column
is called a column matrix.
Example,










31
21
11
a
a
a

18. Diagonal Matrix
• A square matrix all of whose
elements, except those in the
leading diagonal, are zero is called
a diagonal matrix.
Example:










=
nna
a
a
A
00
00
00
22
11

19. Unit Matrix
• A scalar matrix of whose, diagonal
element is unity (or one) is called a Unit
Matrix or an Identity Matrix. A Unit Matrix of
order n is written as .
Example:
mI










=
100
010
001
4I

20. Zero Matrix or Null Matrix
• A matrix, rectangular or square, each of whose
elements are zero is called a Zero Matrix or Null
Matrix.
Denoted by 0.
Example:












=
0000
0000
0000
0000
0

21. Triangular Matrices
• A matrix where the elements are
zero according to the superiority of
the order of their rows (m) and
columns (n) is called a Triangular
Matrix.

22. Upper Triangular Matrix
• If the order of row is greater than the
order of column of an element 0,
then it is called as Upper
Rectangular Matrix.
Example:
nmmn
inij
nj
nj
a
aa
aaa
aaaa
A
×














=
000
00
0 2222
111211

23. Lower Rectangular Matrix
• If the order of row is smaller than the
order of column of an element 0,
then it is called as Lower
Rectangular Matrix.
Example:
nm
aaaa
aaa
aa
a
A
×












=
44434241
333231
2221
11
0
00
000

24. Sub Matrix
• A matrix obtained by deleting some
rows or columns or both of a given
matrix is called a sub matrix of the
given matrix.
Example:
From A= 2x2





=










×
12
13
,
123
132
213
33
Ato

25. Scalar Matrix
• A square matrix when given in the form of
a scalar multiplication to an identity or unit
matrix is called a Scalar Matrix.
• We can also say, a diagonal matrix whose
all diagonal elements are equal is called a
scalar matrix.
Example:






=





=
10
01
0
0
a
a
a
aI

26. Symmetric Matrices
• A symmetric matrix is a special
kind of square matrix A=[aij] for
which,
jandiallforaa jiij −−−−=

27. Symmetric Matrices (cont.)
• Example:










−
−
511
162
125

28. Complex Conjugate of a Matrix
• It is a Matrix obtained by replacing
all its elements by there respective
complex conjugates.
Example:






+
−
=





−
+
=
735
432
,
735
432
.
i
i
Athen
i
i
Aif

29. Skew-symmetric Matrix
• It is square matrix A if,
• The transpose of a square matrix is equal
to negative of that matrix
• Or, we can say a square matrix A is called
a Skew-symmetric Matrix if aij = - aij for all i
and j. In a skew-symmetric matrix all the
diagonal elements are zeroes.
δAAt
−=

30. Skew-symmetric Matrix(cont.)
• Example:





 −
=
06
60
A

31. Matrix
Operations

32. Addition
• Matrices can be added if only they
are of the same order.
• The sum of two (mxn) matrices is
another matrix (mxn) whose
elements are the sum of the
corresponding elements in the
component matrices.

33. Addition (cont.)
• Example:
1
4
2
3
5
8
6
7
+ =
A B+ =

34. 1
4
2
3
5
8
6
7
+ =
6
12
8
10
A B+ = C
Addition (cont.)
• Example:

35. Subtraction
• Matrices can be subtracted if only
they are of the same order.
• The difference of two (mxn)
matrices is another matrix (mxn)
whose elements are the difference
of the corresponding elements in
the component matrices.

36. Subtraction(cont.)
• Example:
1
4
2
3
5
8
6
7
- =
B A- =

37. 1
4
2
3
5
8
6
7
- =
4
4
4
4
B A- = C
Subtraction(cont.)
• Example:

38. Multiplication
• For matrix multiplication,
>the number of columns in the first
matrix or vector must be equal to
the number of rows in the second
matrix or the vector.

39. Multiplication (cont.)
• Example:
1
4
2
3
5
8
6
7
x =
A Bx =

40. Multiplication (cont.)
• Example:
1
4
2
3
5
8
6
7
x =
A Bx = C
(5x1)+ (6x3)
C 1 1
=   A 1 2
xB 2 1k=2
n

41. 1
4
2
3
5
8
6
7
x =
A Bx = C
23 ( 5 x 2 )+ ( 6 x 4 )
C 1 2 =   A 1 k xB k 2k=1
n
Multiplication (cont.)
• Example:

42. 1
4
2
3
5
8
6
7
x =
A Bx = C
23
( 7 x 1 )+ ( 8 x 3 )
34
C 2 1 =   A 2 k xB k 1k=1
n
Multiplication (cont.)
• Example:

43. 1
4
2
3
5
8
6
7
x =
A Bx = C
23 34
( 7 x 2 )+ ( 8 x 4 )31
C 2 2 =   A 2 k xB k 2k=1
n
Multiplication (cont.)
• Example:

44. 1
4
2
3
5
8
6
7
x =
A Bx = C
23 34
31 46
m x n n x p m x p
Multiplication (cont.)
• Example:

45. Inverse of Matrix
• The operation of dividing one matrix
directly by another doesn’t exist in matrix
theory but equivalent of division of unit
matrix by any square matrix can be
accomplished (in most cases) by a
process known as ‘Inversion of Matrix’.
• The concept of inverse matrix is useful in
solving simultaneous equations, input
output analysis and regression analysis.

46. Inverse of Matrix (cont.)

47. Solutions of
simultaneous equations of matrix
no.1
• Using matrices, calculate the values of x and y for
the following simultaneous equations:
2x – 2y – 3 = 0
8 y = 7x + 2

48. Step 1:
• Write the equations in the form
ax + by = c
2x – 2y – 3 = 0 2⇒ x – 2y = 3
8y = 7x + 2 7⇒ x – 8y = –2

49. Step 2:
• Write the equations in matrix form.

50. Step 3:
• Find the inverse of the 2 × 2 matrix.
Determinant = (2 × –8) – (–2 × 7) = – 2

51. Step 4:
Multiply both sides of the matrix
equations with the inverse.
So, x = 14 and y = 12.5

52. Solutions of
simultaneous equations of matrix
no 2:
• Now the aim is to combine the equations
in such a way that we eliminate one of the
variables.

53. Step 1:
• If we multiply the first equation by
some number
• then we can get the coefficient of
the "x" to be the same in both
equations.
• Then we can subtract one equation
from the other and the x-terms will
cancel.

54. Step 2:
• So let's multiply the first equation by 3, so
we have "6x" in both equations:

55. Step 4:
• Thus we are left with an equation that
involves only "y", which we can therefore
rearrange to see what the value of y is:

56. Step 3:
• Now, as planned, we can subtract that
new equation from the second equation
and the x-terms cancel

57. Step 5:
• Having found y, we can substitute it into
either of the two original equations to find
x. Let's substitute it into the first:

58. Step 6:
• Rearranging that equation for x
we can see the value of x:

59. So our result is that
•X = 11 / 7
•Y = 2 / 7.

60. APPLICATION OF MATRIX
IN BUSINESS

61. • Let’s suppose that, we are working for the website
travelocity.com to help people plan trips between
various cities.
• Often the customers are business travelers so that
they want to travel between cities in the morning
to conduct a day’s business.
• Large cities often provide flights to many cities,
but small cities often are quite limited in the
number of cities that they service.
• The customers are particularly interested in travel
between the following cities.
Adjacency matrices and Airlines

62. • The cities are Albany, Boston, New York, Philly,
Wash, Richmond, Detroit, and Las Vegas.
• For simplicity, we will only use the first letter to refer
to the city. Here is the flight information that we
are given.
Adjacency matrices and Airlines

63. • From Boston there are flights to N, P, W, D
• From Albany there are flights to N, W
• From New York there are flights to B, P, W, R, D, L
• From Philly there are flights to N, B, W, R
• From Wash there are flights to B, A, N, R, P, L
• From Richmond there are flights to N, P, W
• From Detroit there are flights to B, N
• From Las Vegas there are flights to N, W
Adjacency matrices and Airlines

64. Now we can represent the flights and the routs
in a very organized way using matrix.
Adjacency matrices and Airlines

65. Adjacency matrices and Airlines
From this chart, the passengers can easily find out
their flights from one city to another.

66. Conclusion
After the discussion given
above, we can conclude that,
• Matrix Algebra is a smart option to
complete different business operations.
• This method can reduce our effort for
preparing different calculations as well
business predictions.