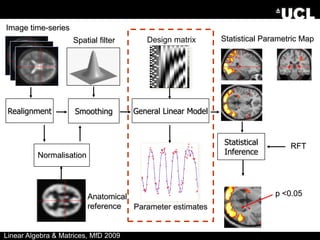
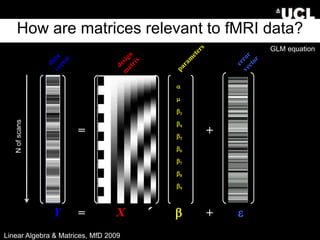
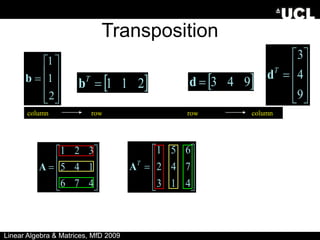
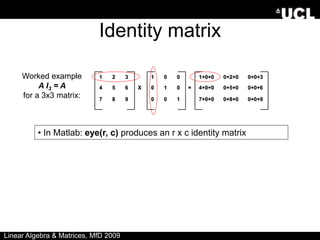
The document provides an overview of linear algebra and matrices. It discusses scalars, vectors, matrices, and various matrix operations including addition, subtraction, scalar multiplication, and matrix multiplication. It also covers topics such as identity matrices, inverse matrices, determinants, and using matrices to solve systems of simultaneous linear equations. Key concepts are illustrated with examples throughout.




![Matrices in Matlab
• X=matrix
• ;=end of a row
• :=all row or column
9
8
7
6
5
4
3
2
1
Subscripting – each element of a matrix
can be addressed with a pair of numbers;
row first, column second (Roman Catholic)
e.g. X(2,3) = 6
X(3, :) =
X( [2 3], 2) =
9
8
7
8
5
“Special” matrix commands:
• zeros(3,1) =
• ones(2) =
• magic(3) =
1
1
1
1
0
0
0
Linear Algebra & Matrices, MfD 2009
2
9
4
7
5
3
6
1
8](https://image.slidesharecdn.com/linearalgebra-221123053144-c81ff78c/85/LinearAlgebra-ppt-6-320.jpg)










![Determinants
•Determinants can only be found for square matrices.
•For a 2x2 matrix A, det(A) = ad-bc. Lets have at closer look at that:
• A matrix A has an inverse matrix A-1 if and only if det(A)≠0.
• In Matlab: det(A) = det(A)
Linear Algebra & Matrices, MfD 2009
a b
c d
det(A) = = ad - bc
[ ]](https://image.slidesharecdn.com/linearalgebra-221123053144-c81ff78c/85/LinearAlgebra-ppt-20-320.jpg)