3.1 Quadratic Functions and Models

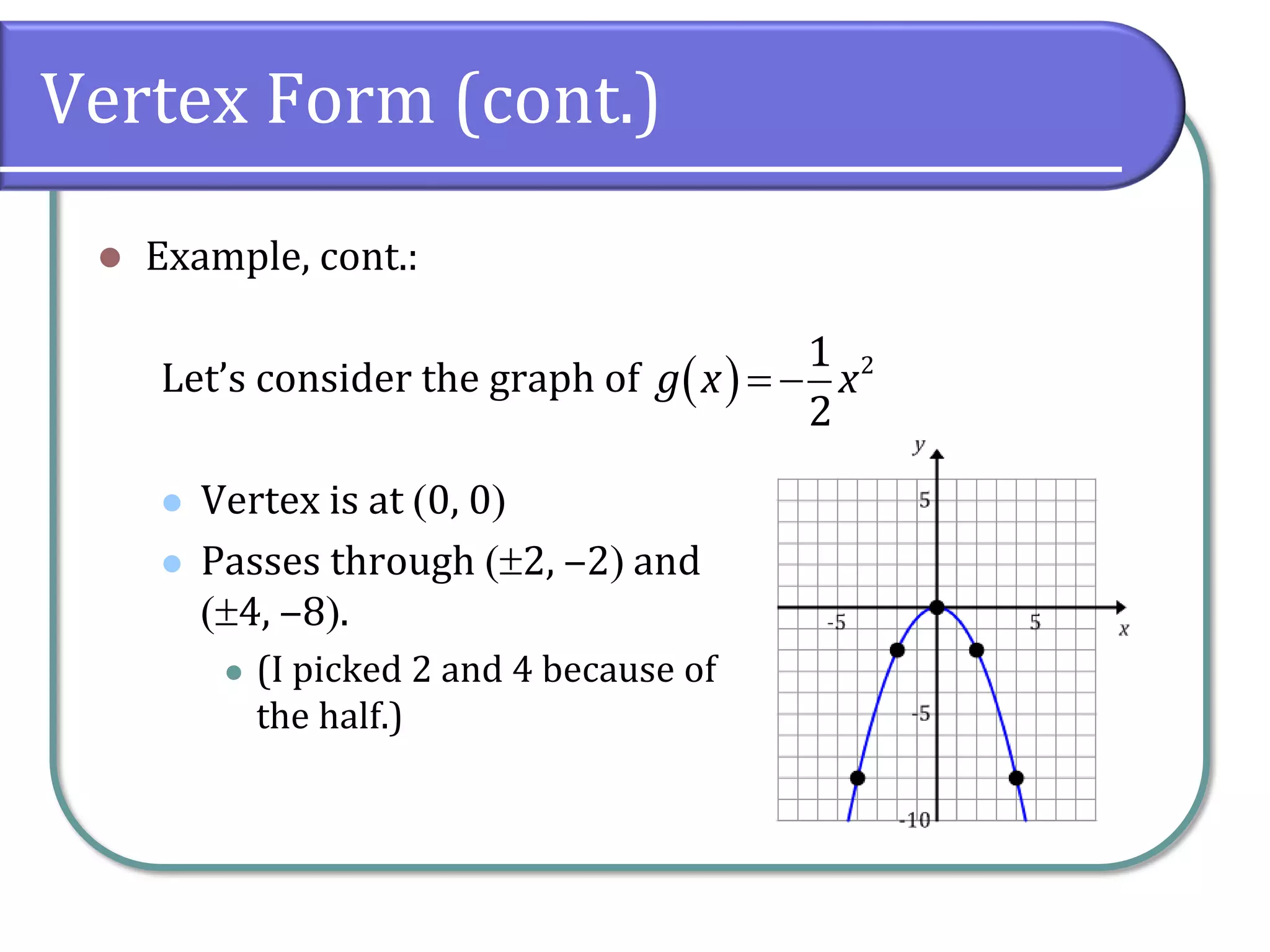
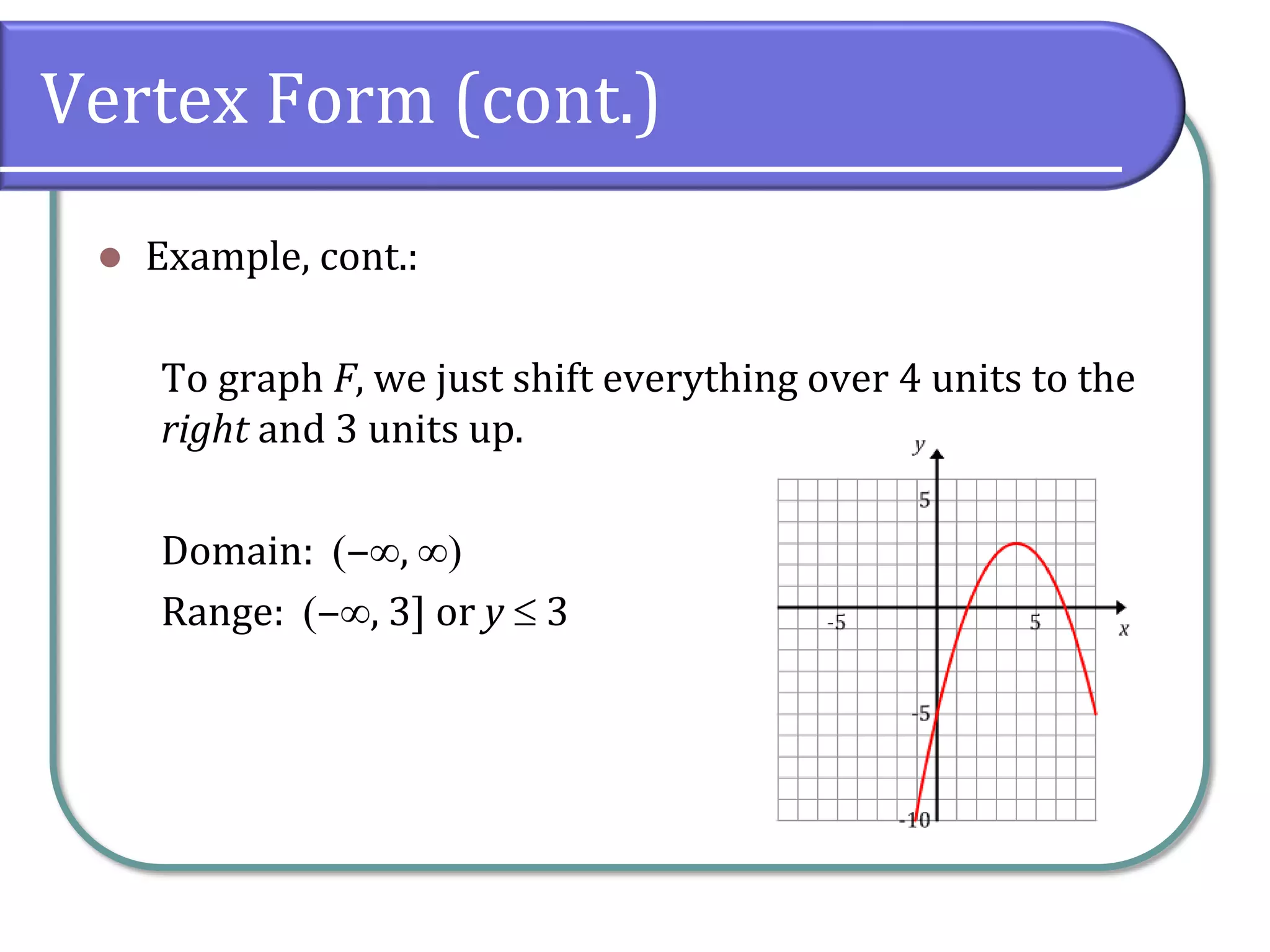
Chapter 3 focuses on quadratic functions and the transformations of their graphs. It covers converting quadratic functions from general to vertex form, identifying the parabola's axis of symmetry and vertex, and the method of completing the square. The chapter includes examples for finding the vertex and practice problems to solidify these concepts.