Embed presentation
Downloaded 63 times


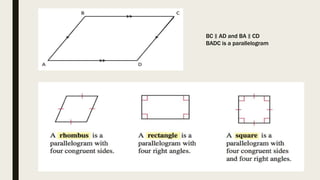

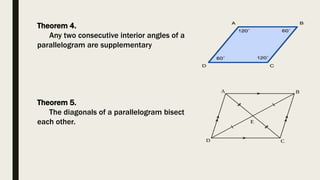
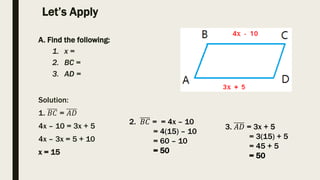
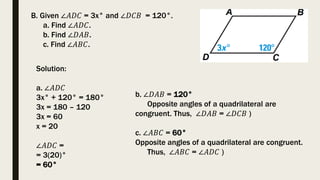
This document defines and provides properties of parallelograms, rectangles, squares, and rhombuses. It states that a parallelogram is a quadrilateral with both pairs of opposite sides parallel. A rectangle is a parallelogram with right angles, and a square is a rectangle with all sides congruent. A rhombus is a parallelogram with all sides equal. It then provides 5 theorems about parallelograms, including that diagonals bisect each other and opposite angles are congruent. An example problem applies these properties to find missing angle and side measures.






