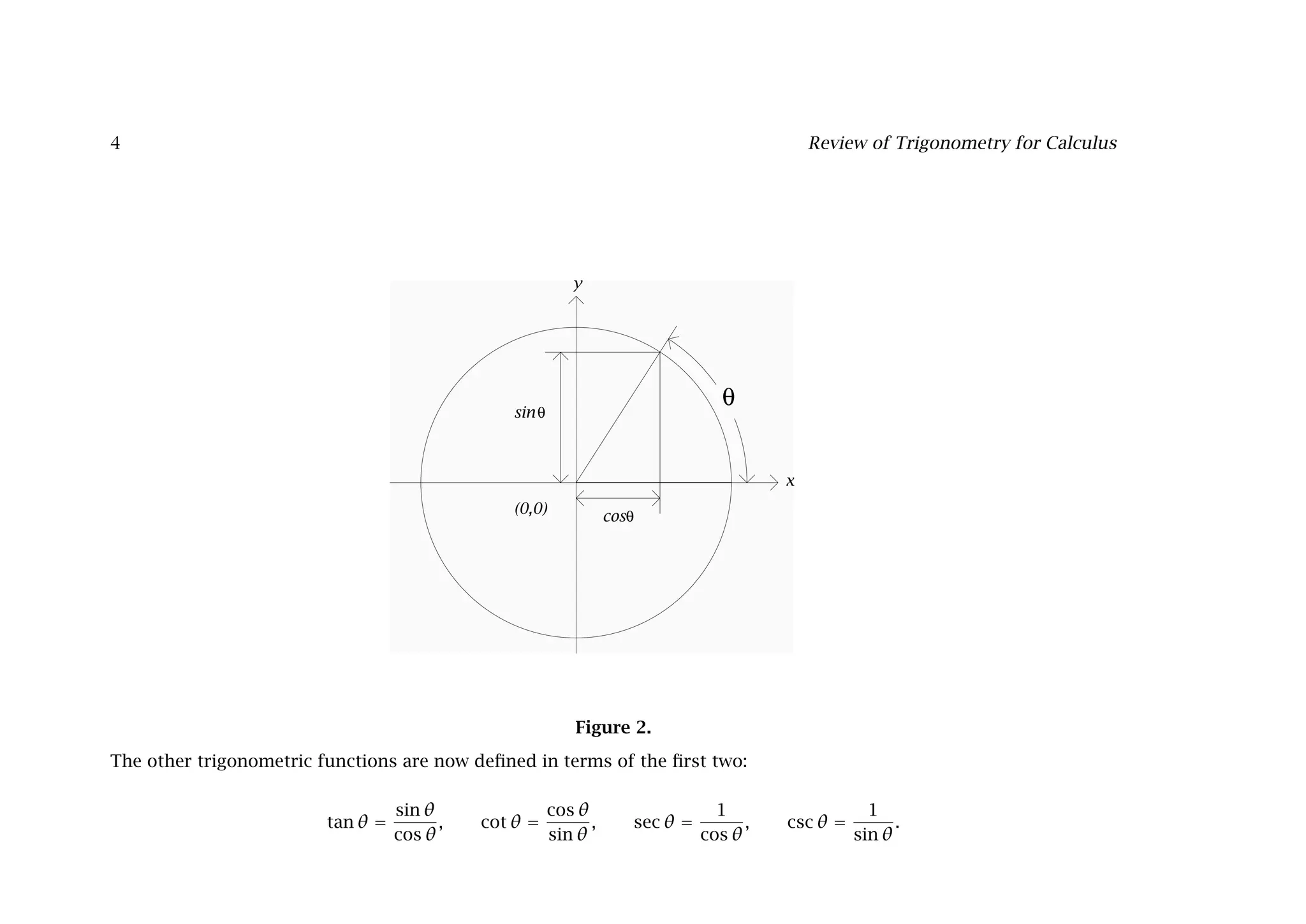
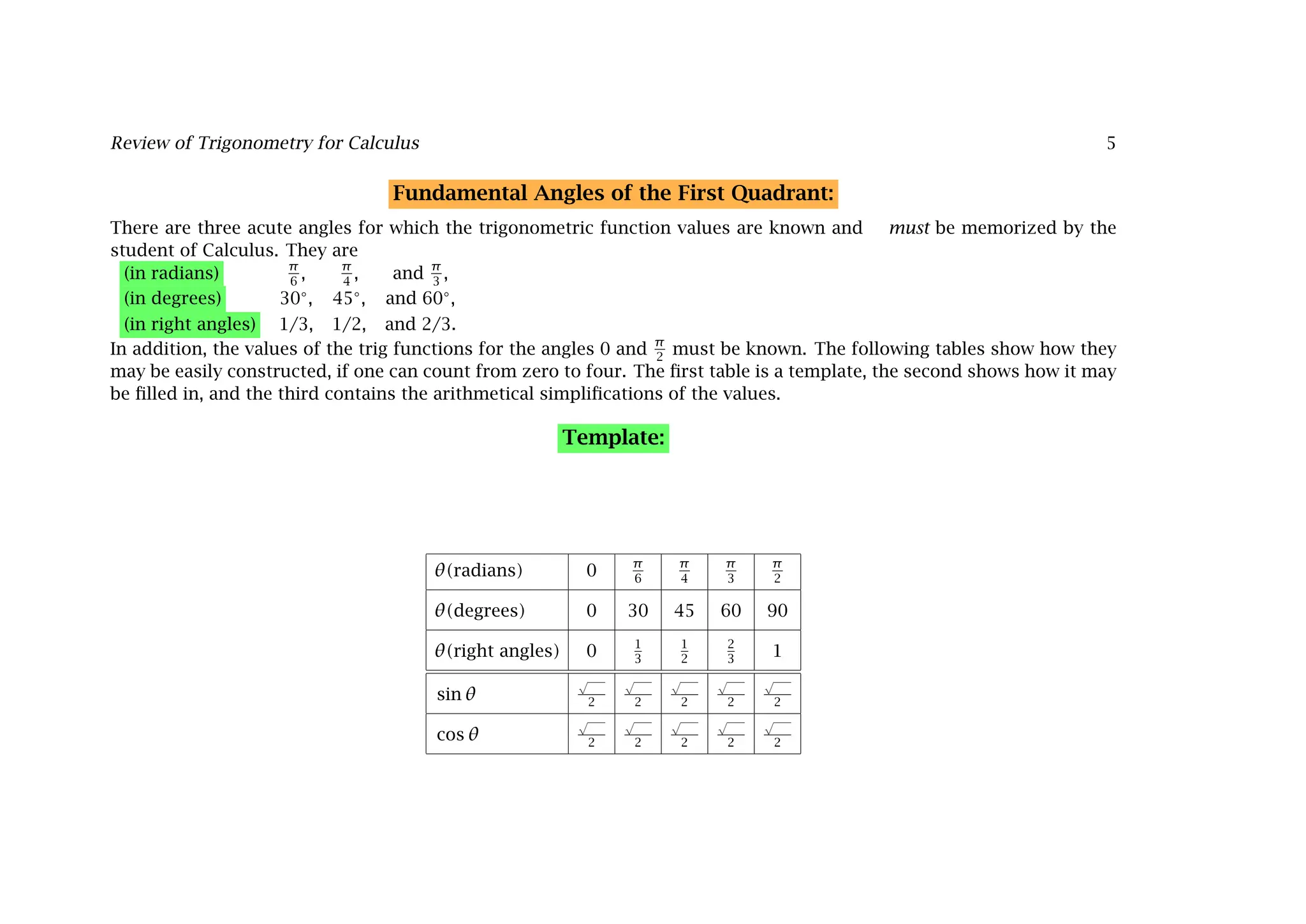
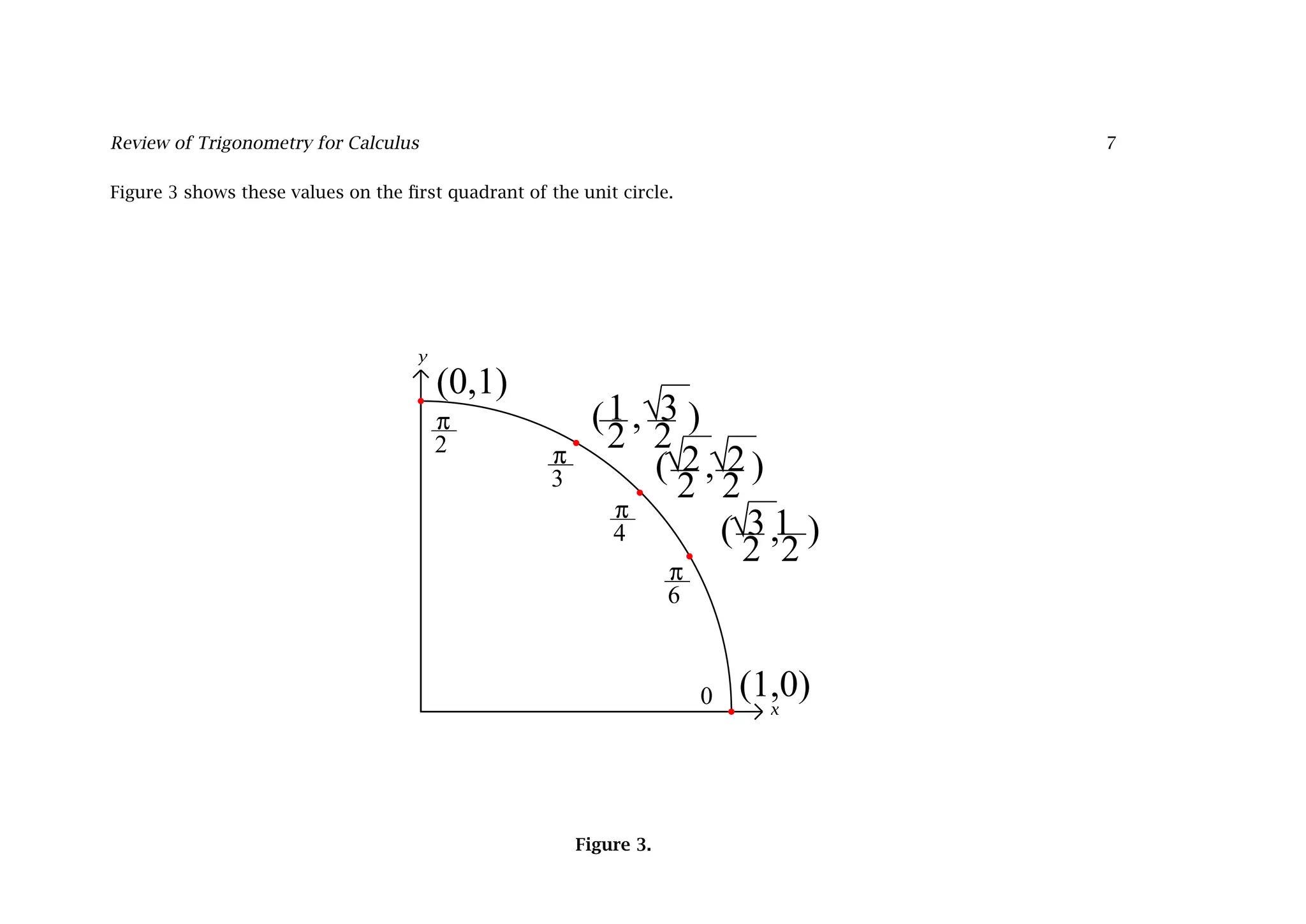
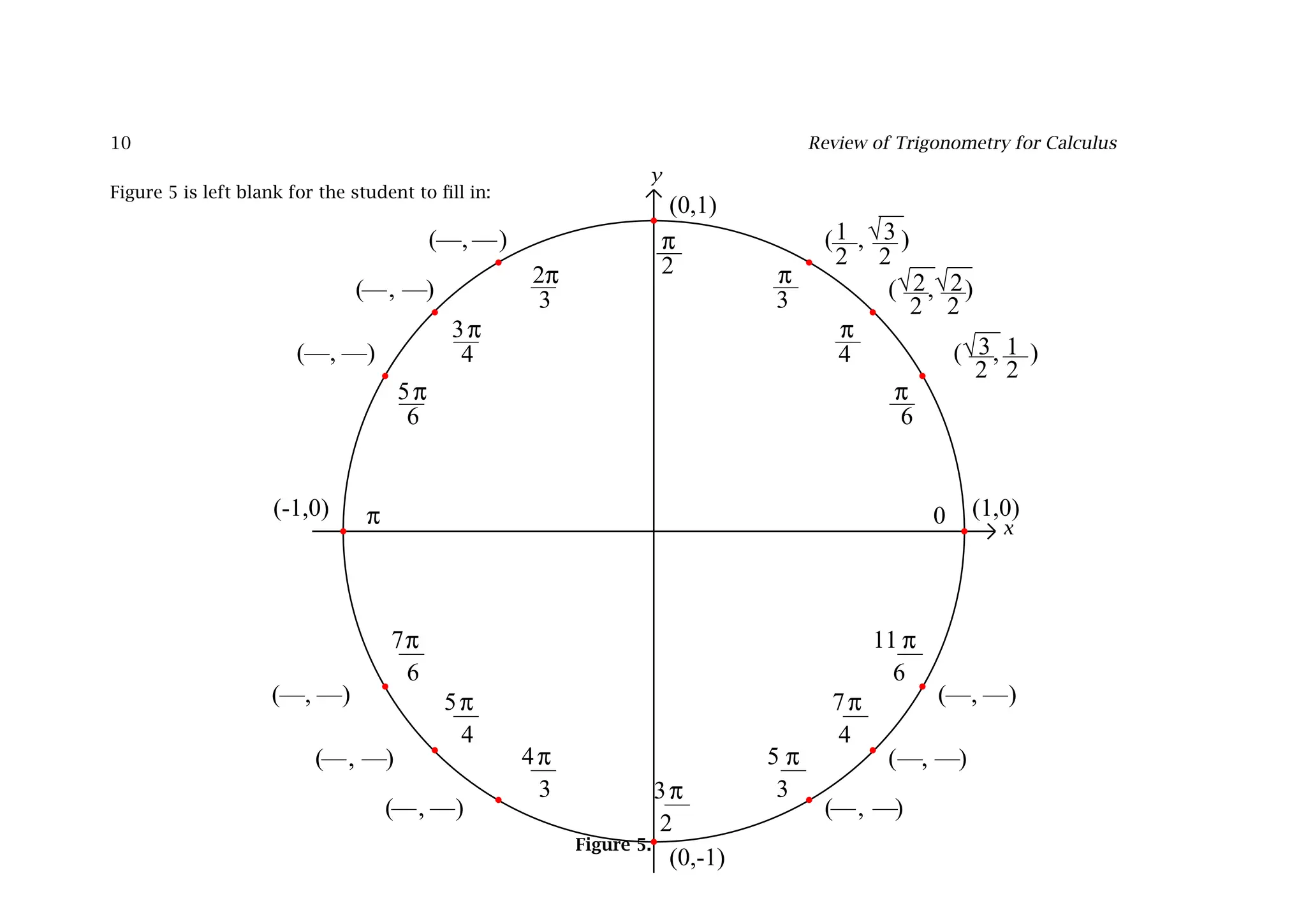
This document provides a comprehensive overview of trigonometry in the context of calculus, explaining definitions, functions, and their relationships using the unit circle. It details fundamental angles, trigonometric identities, and the connections between trigonometric functions such as sine, cosine, and tangent, including their periodicity. The document also emphasizes the importance of the radian as the preferred unit of angle measurement in calculus.