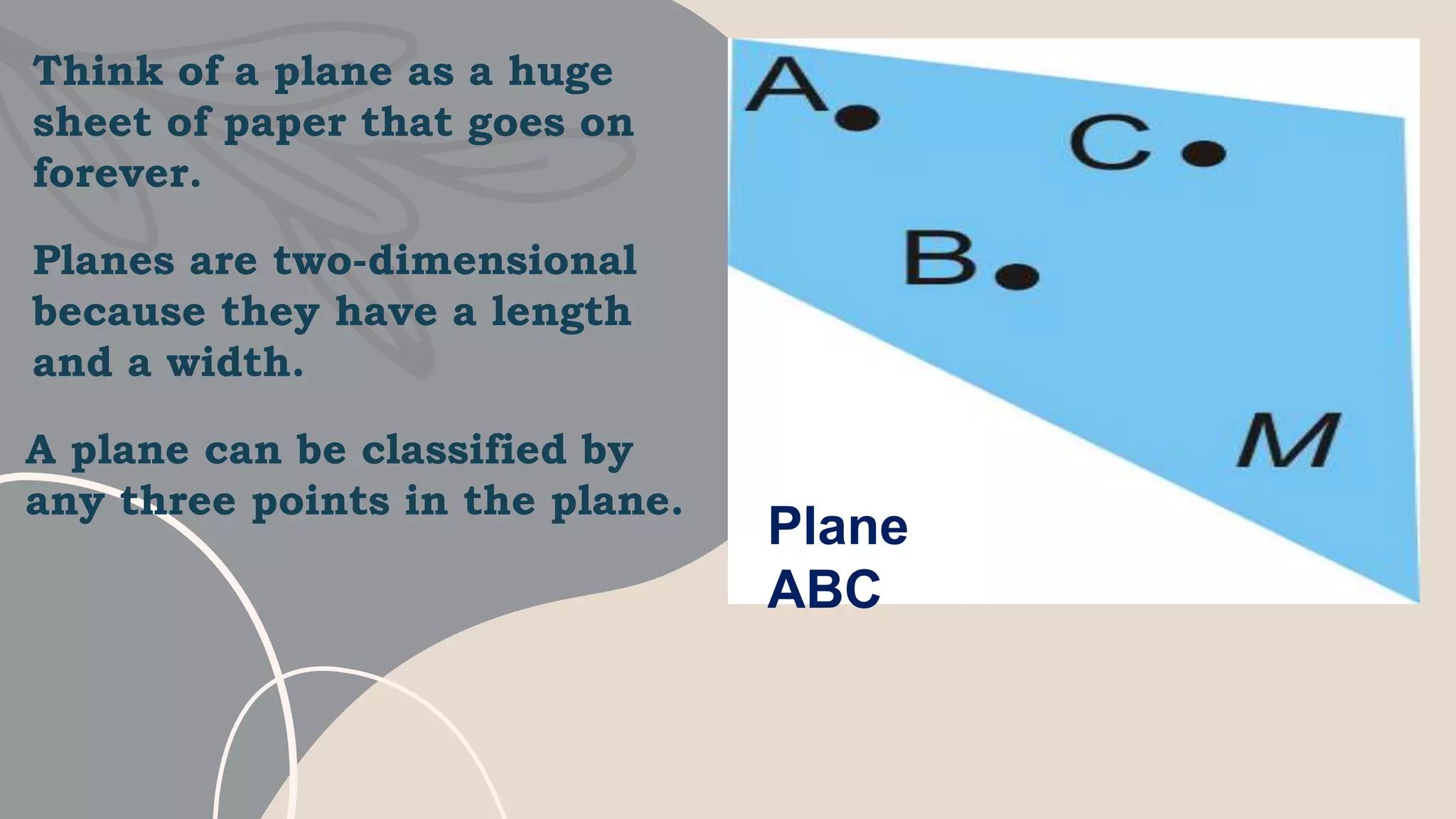
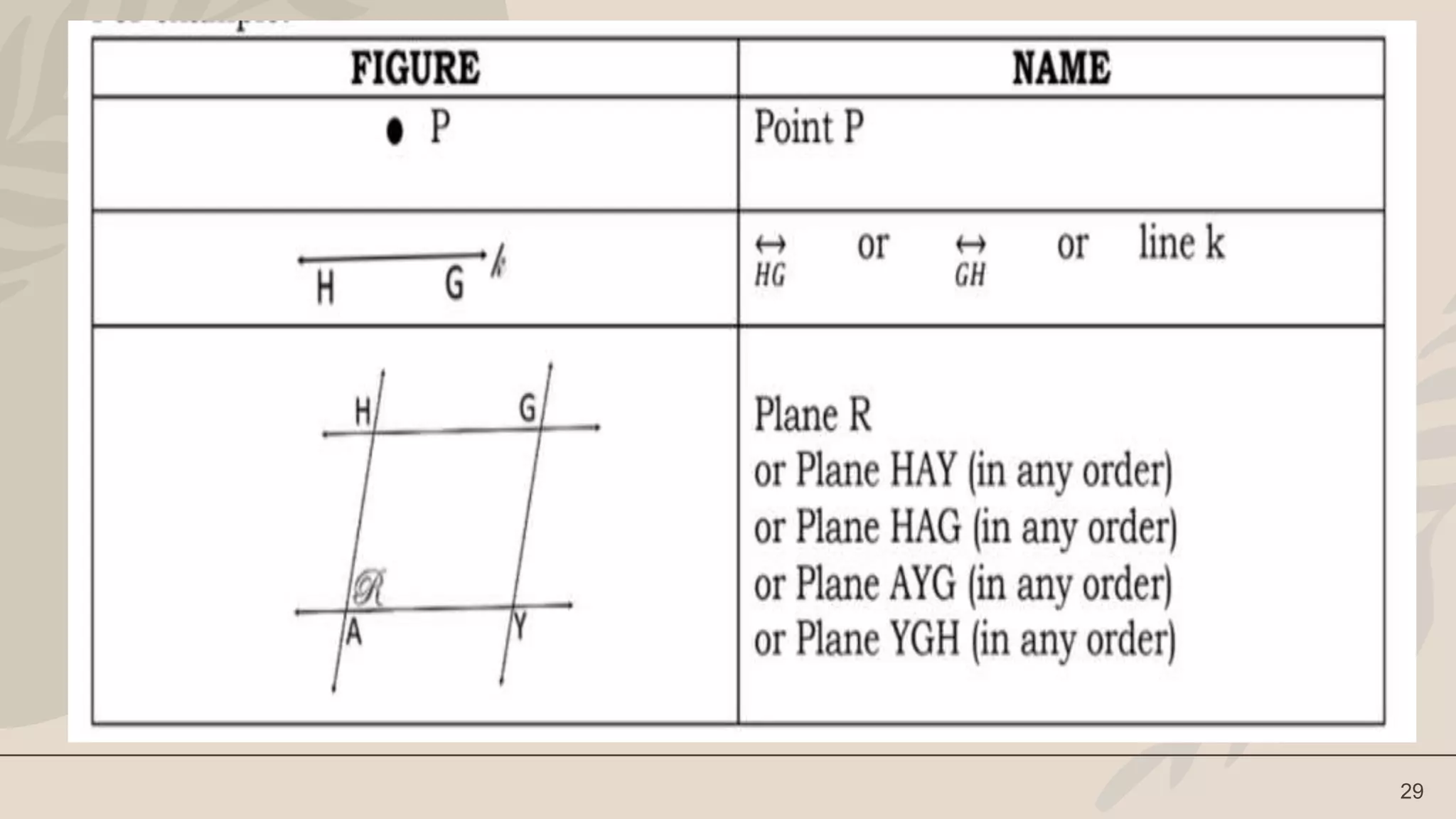
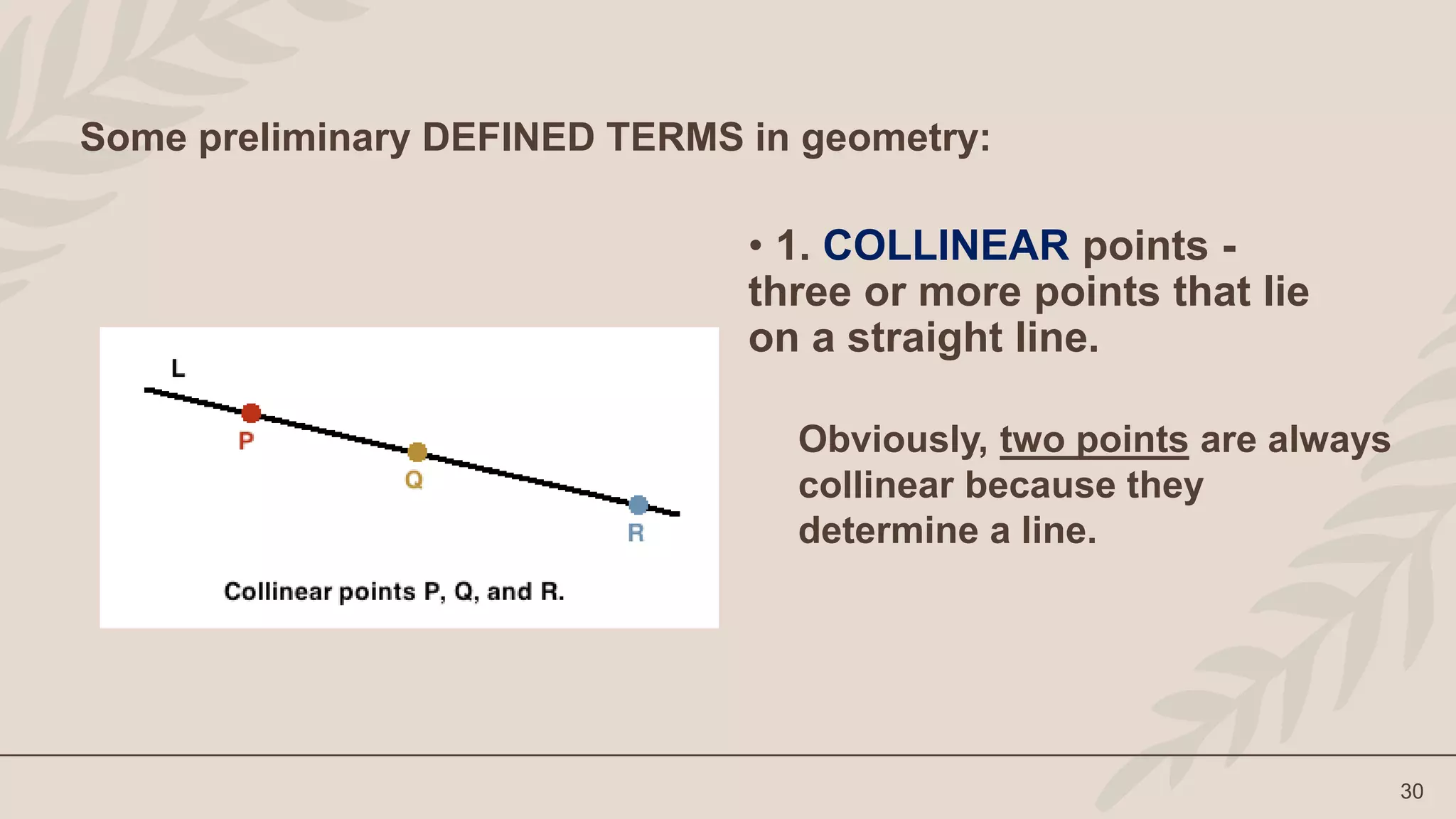
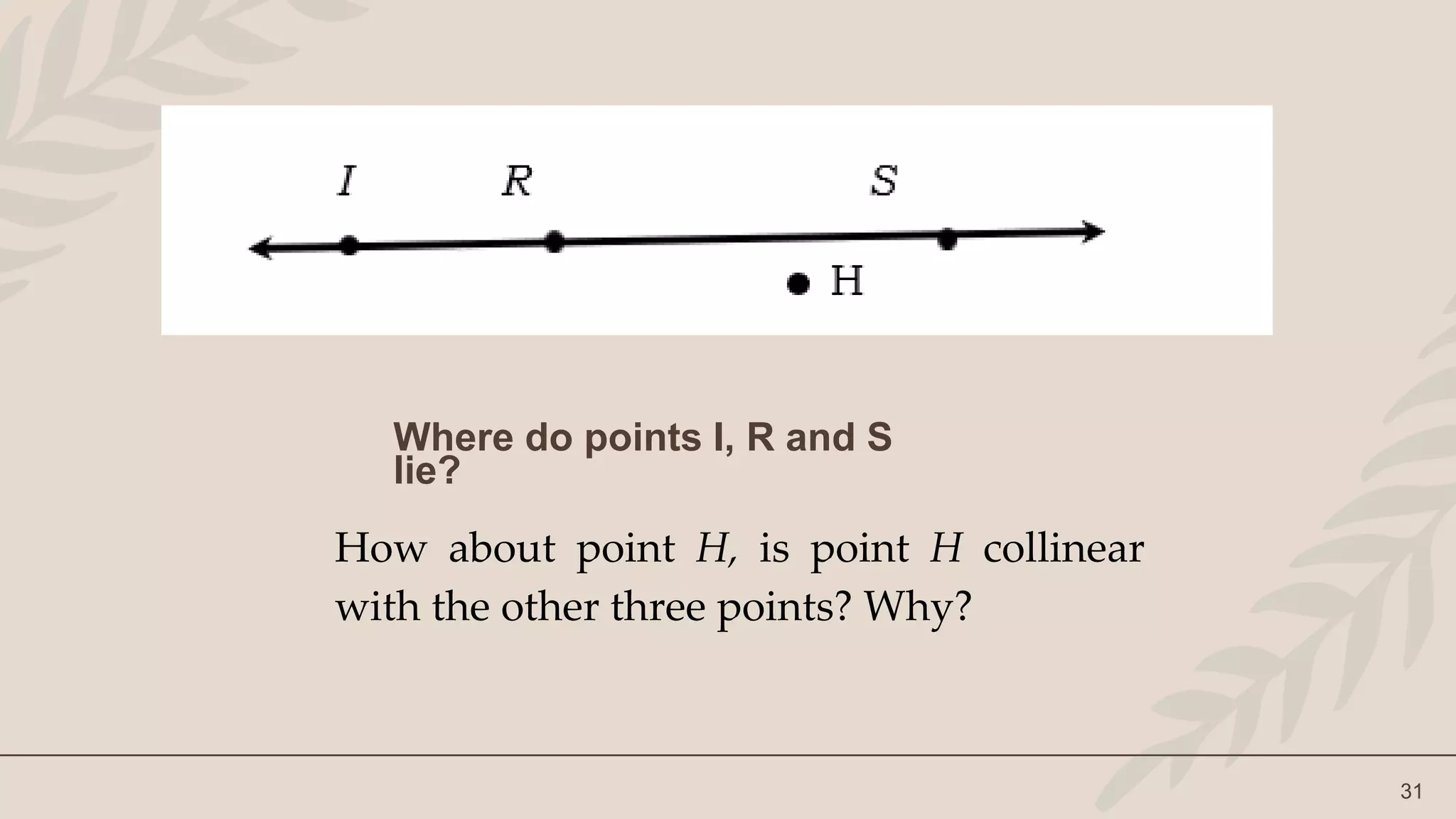
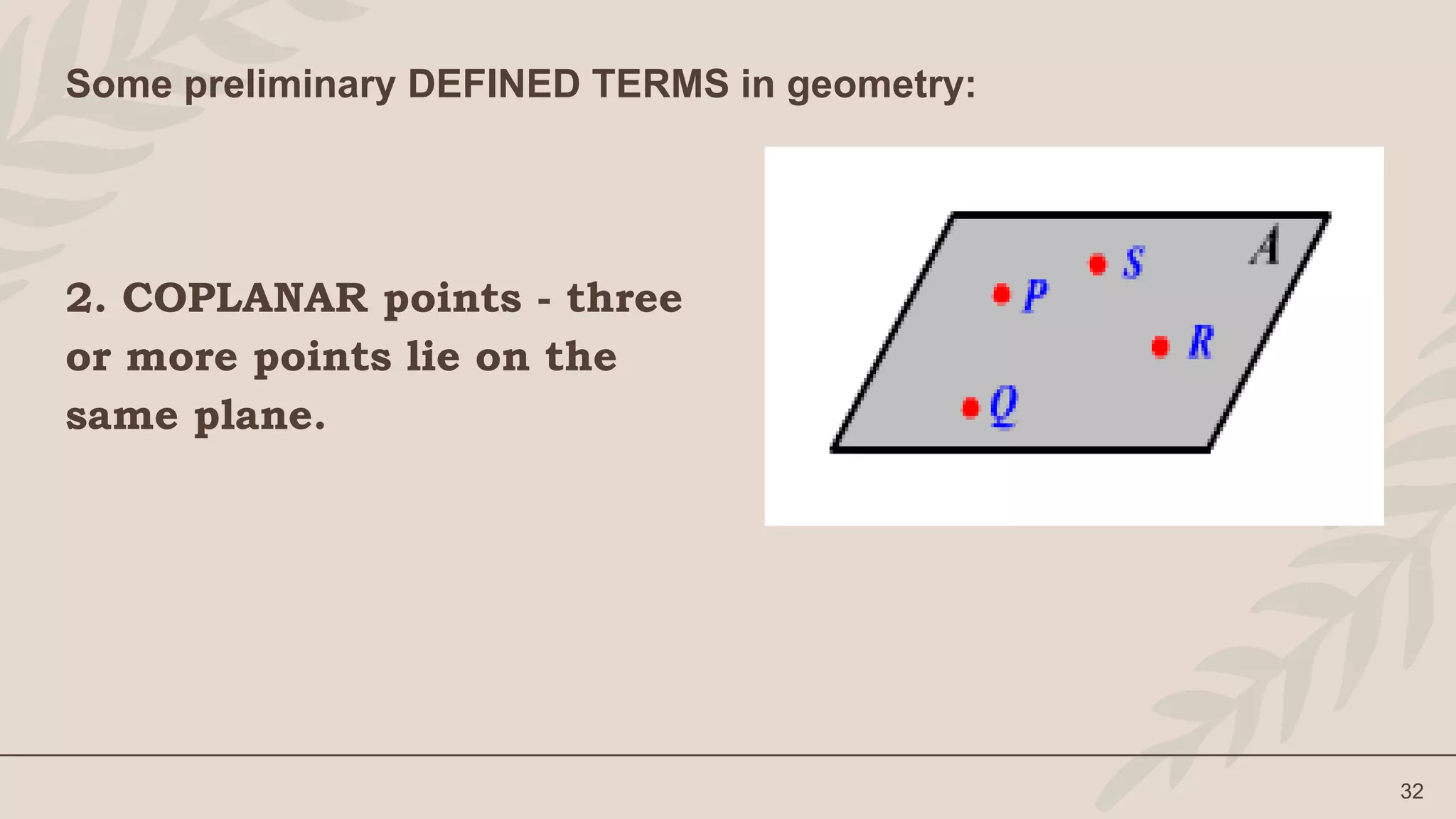
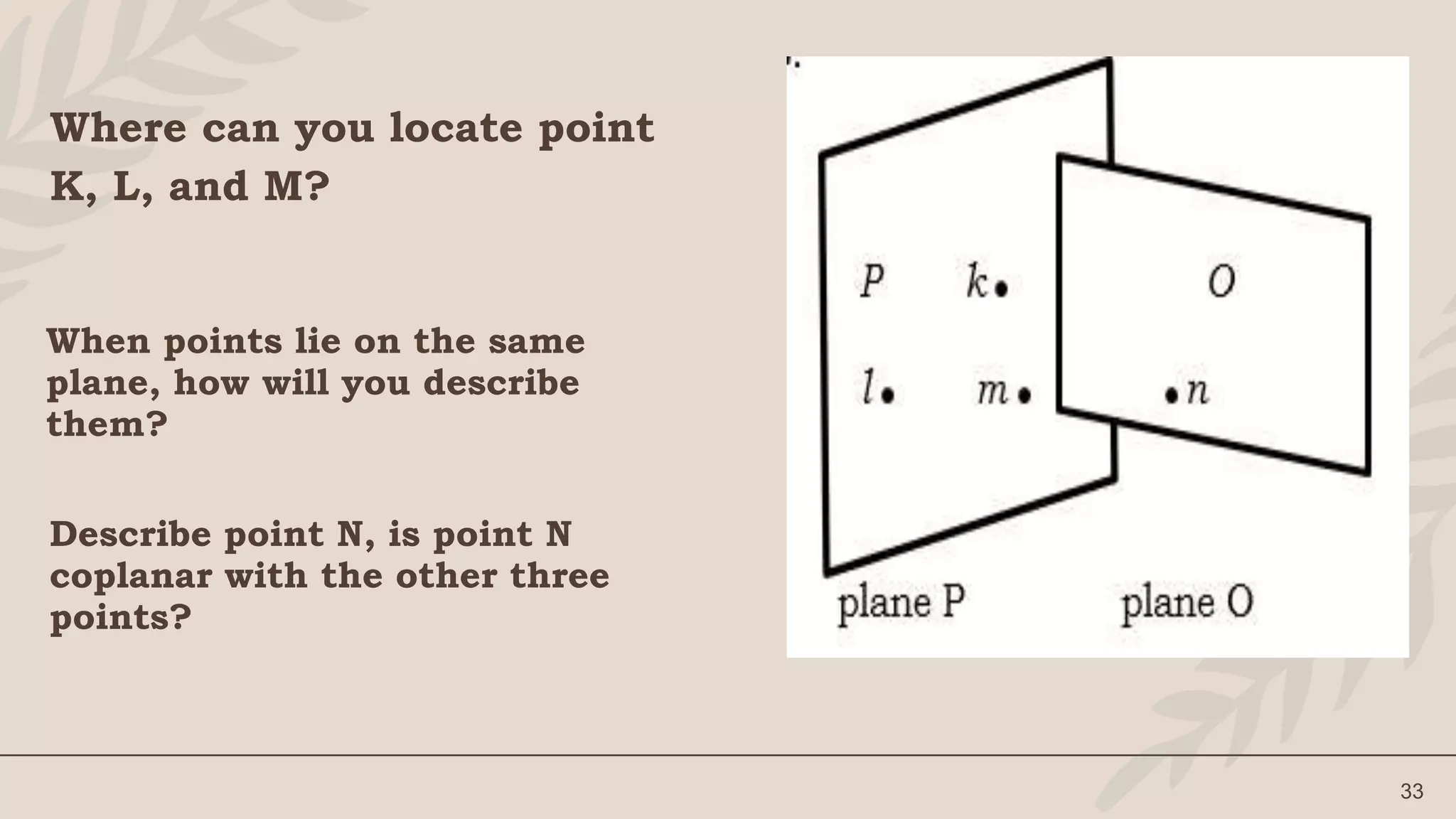
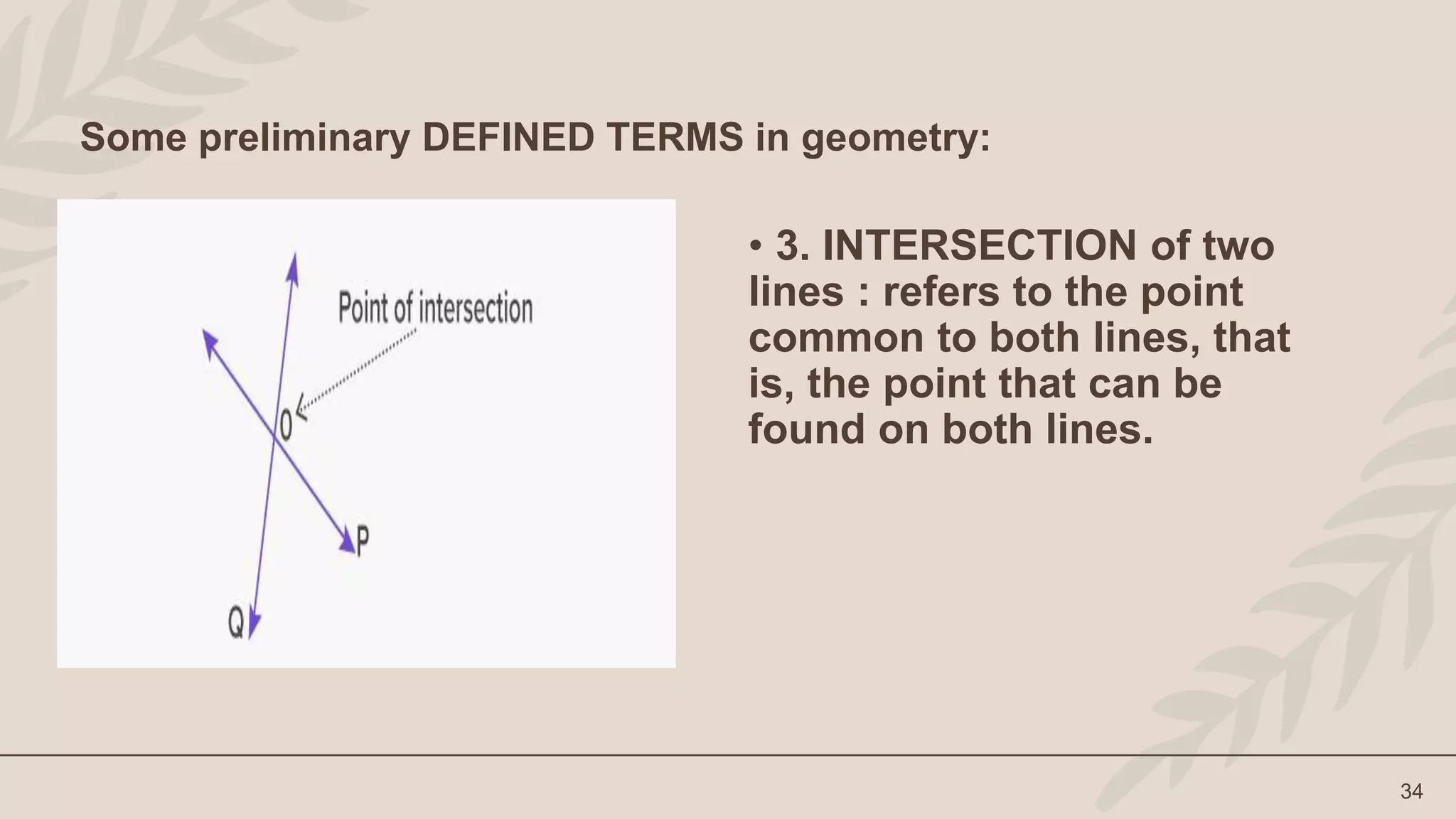
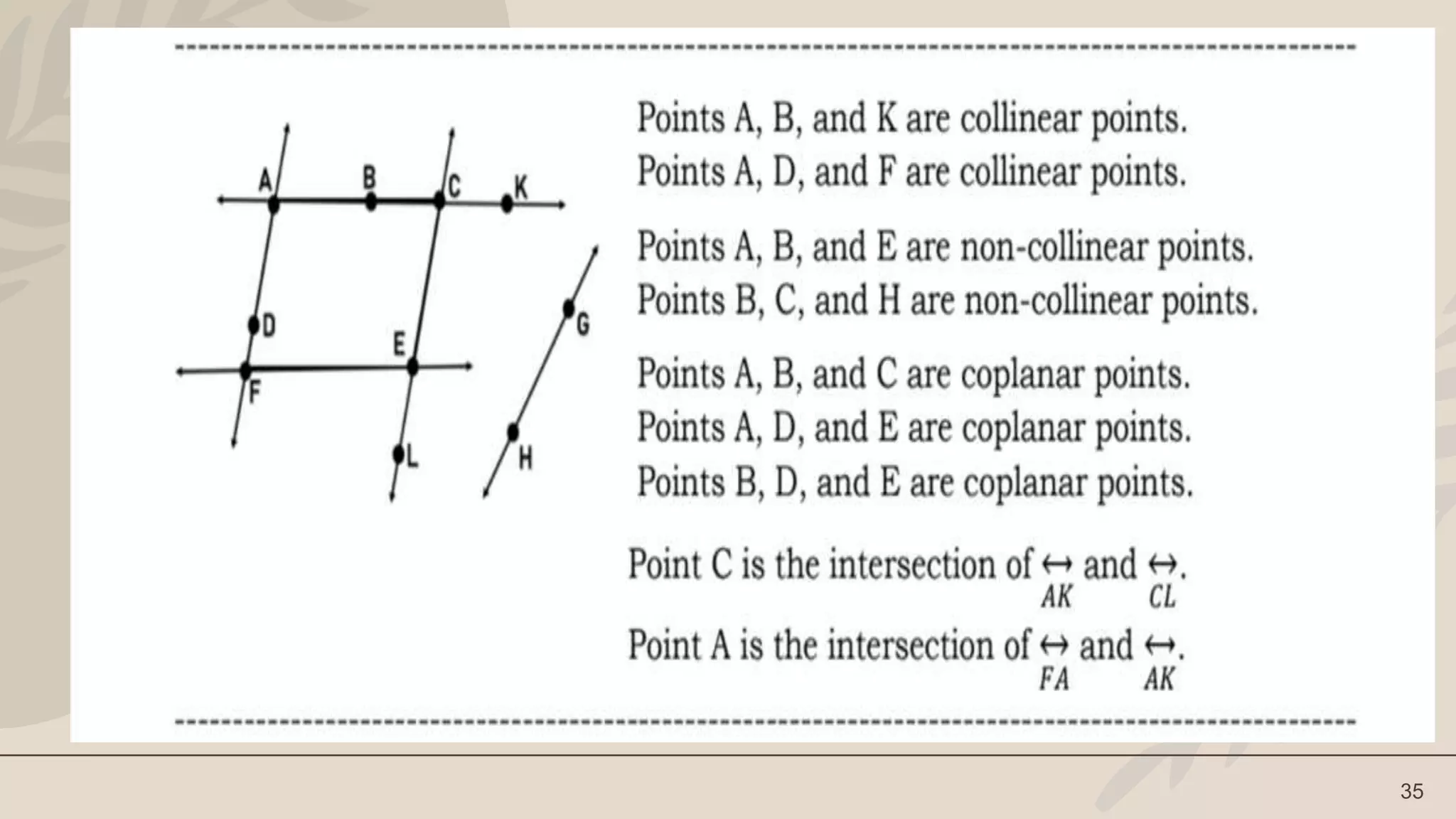
This document appears to be a lesson plan on basic undefined and defined terms in geometry. The objectives are to: 1. Determine basic undefined terms like point, line, and plane and defined terms. 2. Name basic geometric figures appropriately. 3. Represent points, lines, and planes using models. The lesson defines terms like point, line, plane and their representations. It discusses undefined terms like point, line, and plane and defined terms like collinear points and coplanar points. Examples and illustrations are provided to explain the concepts. Activities like naming figures and determining if statements are true or false are included for student practice.

1. Undefined
and
Defined
Terms of
Geometry
Name of Teacher
Subject

2. OBJECTIVES
After going through this
lesson, you are expected to:
1. Determine the different
basic undefined and defined
terms of geometry;
2. Name the different basic
geometric figures
appropriately; and
3. Represent point,
line, and plane using
concrete pictorial
models

3. 3

4. 4
What did the
architect use in
designing the
building?

5. 5
What did the
architect use in
designing the
building?

6. 6
What did the
architect use in
designing the
building?

7. 7
What did he consider in
creating attractive
patterns?

8. 8
What did he consider in
creating attractive
patterns?

9. 9
What did he consider in
creating attractive
patterns?

10. 10
What is
Geometry?

11. 11
What is
Geometry?

12. 12
Geometry is a branch of
mathematics that deals with
the study of shapes, sizes,
figures, spaces, and all
quantities related to the things
you see on Earth.

13. 13
Why do
we do
Geometry
?

14. 14
We do geometry to discover
patterns, find areas,
volumes, lengths and angles,
and better understand the
world around us.

15. 15
The word geometry is a
conglomeration of the Greek
words “geo” and “metron”.
Geo : means “Earth”
Metron: means “measurement”

16. 16
In short, geometry is
the mathematical
study of Earth
measurement.

17. Geometry is grounded on the
idea that everything around
us is made up of smaller
geometric units called points,
lines, and planes.

18. 18
Euclid
of Alexandria,
Egypt
The Father of
Geometry

19. •Points, lines, and
planes are collectively
called UNDEFINED
TERMS.
19
because of the obvious idea
that it is not possible to
define them formally

20. 20
Students, close your eyes
and imagine the stars in the
sky at night. Then open your
eyes how do the stars in the
sky look like?

21. POINT
❖ Has NO part.
❖ Has position but with NO spatial magnitude, size, or
dimension.
❖ Has NO width.
❖ Has NO thickness.
❖ Can be represented by a small dot on paper using the
tip of the pencil.
❖ Locations of places on a map are also an example of points.

22. 22
These points are said “Point
A,” “Point L”, and “Point F.”
Points are labeled with a
CAPITAL letter.

23. 23

24. 24
LINE
❑ Is a geometric figure which has NO width.
❑ Has NO thickness.
❑ Is a geometric figure which has NO width.
❑ Extends indefinitely in opposite directions.
❑ Can be imagined to be a very long pencil or rope where
the starting point and the ending point cannot be seen.

25. 25
o Line PQ
o Line g
A line, like a point, does not take up space. It
has direction, location and is always straight.
Lines are one-dimensional because they
only have length (no width).
A line can be named or identified using
any two points on that line or with a
lower-case, italicized letter.

27. PLANE
❖ Is a surface which lies evenly with straight
lines on itself.
❖ Is a two-dimensional (2-D) figure that HAS
length and width.
❖ Has NO thickness.
❖ Some physical models of a plane include wall,
floor, and window.

28. Plane
ABC
Think of a plane as a huge
sheet of paper that goes on
forever.
Planes are two-dimensional
because they have a length
and a width.
A plane can be classified by
any three points in the plane.

29. 29

30. • 1. COLLINEAR points -
three or more points that lie
on a straight line.
30
Some preliminary DEFINED TERMS in geometry:
Obviously, two points are always
collinear because they
determine a line.

31. Where do points I, R and S
lie?
31
How about point H, is point H collinear
with the other three points? Why?

32. 2. COPLANAR points - three
or more points lie on the
same plane.
32
Some preliminary DEFINED TERMS in geometry:

33. Where can you locate point
K, L, and M?
33
When points lie on the same
plane, how will you describe
them?
Describe point N, is point N
coplanar with the other three
points?

34. • 3. INTERSECTION of two
lines : refers to the point
common to both lines, that
is, the point that can be
found on both lines.
34
Some preliminary DEFINED TERMS in geometry:

35. 35

36. 36
Are you ready?

37. 37
Corner of a room

38. 38

39. Cable Wire
39

40. 40

41. Board
41

42. 42

43. Cover of a Book
43

44. 44

45. 45
Tip of a pencil

46. 46

47. 20XX presentation title 47
Floor

48. 48

49. 49
Floor

50. 50

51. 51
Edge of a building

52. 52

53. 53
Skipping rope

54. 54

55. 55
Retina of an eye

56. 56

57. 57
Give your
own
example

58. 58
Give your
own
example

59. 59
Illustrate Me!
1. Illustrate the intersection of two lines. What is their intersection?
Label the lines and the intersection.
2. Illustrate intersecting line and plane. What is the intersection? Label
the figure.
3. Illustrate intersecting line and plane. What is the intersection? Label
the figure.

60. 60
Illustrate Me!
1. Illustrate the intersection of two lines. What is their intersection?
Label the lines and the intersection.
2. Illustrate intersecting line and plane. What is the intersection? Label
the figure.
3. Illustrate intersecting line and plane. What is the intersection? Label
the figure.

61. 61
Let us Play: tic tac toe
Two players will compete. The first who can make five consecutive
points in a line will be the winner. First round put all your dots on the
plane. Block the way of your opponent and aim to put all your dots on
a line. If there’s no five consecutive dots formed, move your dots with
the same goal, one step at a time. Be wise to win!

62. 62
Let us Play: tic tac toe
Two players will compete. The first who can make five consecutive
points in a line will be the winner. First round put all your dots on the
plane. Block the way of your opponent and aim to put all your dots on
a line. If there’s no five consecutive dots formed, move your dots with
the same goal, one step at a time. Be wise to win!

63. 63
• A point is named using a capital
letter.
• A line is named using two capital
letters representing any two points
that lie on the line or using a
lowercase script letter. The line
notation using two points also
includes a double-headed arrow ( )
above of the two capital letters.
A plane is named using a single script
uppercase letter or using any three
points on the plane that do not lie on
a straight line, in no specific order.

64. 64
COLLINEAR points - three or more points
that lie on a straight line. Obviously, two
points are always collinear because they
determine a line.
COPLANAR points - three or more points
lie on the same plane.
INTERSECTION of two lines : refers to the
point common to both lines, that is, the
point that can be found on both lines.

65. A. Name me! Identify what is asked on the following:
1. It is a flat surface that extends infinitely in all
directions.
2. Points that lie on the same line.
3. It is a specific location in space that has no
dimensions.
4. Points that lie on the same plane.
5. It is of infinite length, but it is no width and no
thickness.
65
GROUP A:

66. B. Tell whether each represents a point, a line or a plane.
1. Your desktop
2. The surface of the page of a notebook.
3. The string on a guitar.
4. The ceiling of a room.
5. A broomstick.
6. Electric wire.
7. The floor.
8. A hair strand.
9. A rope.
10. A needle point.
66
GROUP B:

67. C. Give the appropriate name of the following geometric
figures.
67
GROUP C:

68. D. TRUE or FALSE. Write T if the statement is true. If
false, write F.
20XX presentation title 68
GROUP D:

69. 69
ASSIGNMENT
1.Subset of a line.
2.Segment addition postulate.

70. 70