Lesson 15: Geometry

𝐏𝐓𝐒 𝟑
Bridge to Calculus Workshop
Summer 2020
Lesson 15
Geometry
“Dividing one number by another is
mere computation; knowing what to
divide by what is mathematics."
– Jordan Ellenberg -

Lehman College, Department of Mathematics
Linear Functions and Lines (1 of 4)
Example 1. A phone company offers two monthly
charge plans. In Plan A, the customer pays a monthly
fee of $3.40 and then an additional 8 cents per minute
of use. In Plan B, there is no monthly fee, but the
customer pays 9 cents per minute of use.
For what amounts of monthly phone use will Plan A cost
more than Plan B? Use 𝑥 for the number of minutes of
phone use in a month and solve your inequality for 𝑥.
Solution. Let 𝑦 be the monthly cost in dollars, then:
Plan A costs more than Plan B:
It follows that:
𝑦 = 0.08𝑥 + 3.40 𝑦 = 0.09𝑥For plan A: For plan B:
0.08𝑥 + 3.40 > 0.09𝑥
3.40 > 0.01𝑥 or 𝑥 < 340

Example 1. Suppose that a household's monthly water
bill (in dollars) is a linear function of the amount of water
the household uses (in hundreds of cubic feet, HCF).
When graphed, the function gives a line with a slope of
1.5 . See the figure below.
If the monthly cost
for 10 HCF is $32,
what is the monthly
cost for 16 HCF?

Solution. Let 𝑥 represent the monthly water usage (in
HCF) and let 𝑦 represent the monthly cost (in dollars).
Since the relation between 𝑥 and 𝑦 is linear, then we
can represent 𝑦 using the slope-intercept form of the
equation of a nonvertical line, given by the formula:
where 𝑚 is the slope and 𝑏 is the 𝑦-intercept.
Solution. In the given problem, 𝑚 = 1.5 = 3/2. Hence,
its equation is given by:
We know that the line passes through the point (10, 32).
𝑦 = 𝑚𝑥 + 𝑏
𝑦 =
3
2
𝑥 + 𝑏

Solution (cont’d). From the previous slide:
Since 𝑏 = 17, then:
When 𝑥 = 16, we have:
It follows that the monthly cost for 16 HCF is:
𝑦 =
3
2
𝑥 + 17
𝑦 =
3
2
𝑥 + 𝑏 Write equation of line
Substitute the point (10, 32)32 =
3
2
(10) + 𝑏
32 = 15 + 𝑏
17 = 𝑏
Simplify
𝑦 =
3
2
16 + 17 = 41
$41

Similar Triangles (1 of 2)
Example 2. A student wants to measure the height of a
tree. She sights the top of the tree, using a mirror that is
lying flat on the ground. The mirror is 30 ft from the tree,
and the student is standing 6 ft from the mirror, as
shown in the figure. Her eyes are 5 ft above the ground.
How tall is the tree? Round your answer to the nearest
foot. (The figure is not drawn to scale.)

Similar Triangles (2 of 2)
Solution. The two triangles are similar because:
They both have two angles of the same measure.
Therefore, the ratios of corresponding sides are equal:
Let ℎ be the length of side 𝐴𝐵, then:
ℎ
5
=
30
6
= 5 It follows that: ℎ = 25 ft

Perimeter Problems (1 of 2)
Example 3. A garden is formed by joining a rectangle
and a semicircle, as shown below. The rectangle is 30 ft
long and 20 ft wide. If the gardener wants to build a
fence around the garden, how many feet of fence are
required? (Use the value 3.14 for 𝜋, and do not round
your answer. Be sure to include the correct unit in your
answer.)

Perimeter Problems (2 of 2)
Solution. Consider the perimeters separately:
Radius of circle:
Half circumference of circle:
Perimeter of part of rectangle:
Perimeter of garden:
𝑟 = 10 ft
1
2
2𝜋𝑟 = 𝜋𝑟
= 3.14(10) = 31.4 ft
30 + 20 + 30 =
80 + 31.4 = 111.4 ft
80 ft

Area Problems (1 of 2)
Example 4. A training field is formed by joining a
rectangle and two semicircles, as shown below. The
rectangle is 100 m long and 20 m wide. Find the area of
the training field. (Use the value 3.14 for 𝜋, and do not
round your answer. Be sure to include the correct unit in
your answer.)

Area Problems (2 of 2)
Solution. Join the semicircles together as one circle:
Radius of circle:
Area of circle:
Area of rectangle:
Total area of field:
𝑟 = 10 m
𝜋𝑟2
= 𝜋(10)2
= 100𝜋
= 100(3.14) = 314 m2
100(20) = 2,000 m2
2,000 + 314 = 2,314 m2

Volume Problems (1 of 2)
Example 5. A company sells its corn flakes in two
boxes of different sizes: the regular box and the family
value box. For the family value box, the length of the
box has been increased by 15%, the height has been
increased by 20%, and the width remains the same.
By what percentage does the volume of the box
increase from the regular box to the value box? Round
your answer to the nearest percent.
Solution. Consider the regular boxes to be a cuboid of
length 𝑙, height ℎ and width 𝑤.
Let 𝑉1 represent the volume of the regular box and let 𝑉2
be the volume of the family box.

Solution (cont’d). The volume 𝑉1 of the regular box is
given by the formula:
The new length is given by 1.15𝑙, and the new width by
1.20𝑤. It follows that the volume 𝑉2 of the family box:
The ratio of the volumes:
It follows that the volume of the box increased by:
𝑉1 = 𝑙 ⋅ ℎ ⋅ 𝑤
𝑉2 = (1.15𝑙) ⋅ ℎ ⋅ (1.20𝑤)
𝑉2
𝑉1
=
(1.15𝑙) ⋅ ℎ ⋅ (1.20𝑤)
𝑙 ⋅ ℎ ⋅ 𝑤
= 1.15 ⋅ 1.20 = 1.38
38%

Example 6. A food company distributes its tomato soup
in two cans of different sizes. For the larger can, the
diameter has been increased by 30%, and the height
remains the same.
By what percentage does the volume of the can
increase from the smaller can to the larger can? Round
your answer to the nearest percent.
Solution. Consider the smaller can to be a right circular
cylinder with base diameter 𝑑, radius 𝑟, and height ℎ.
The radius 𝑟 of the can increases by the same 30%.
Let 𝑉1 represent the volume of the smaller can and let
𝑉2 be the volume of the larger can.

Solution (cont’d). The volume 𝑉1 of the smaller can is
given by the formula:
The new radius is given by 1.30 ⋅ 𝑟, and the height
remains ℎ. Hence, the volume 𝑉2 of the larger can:
The ratio of the volumes:
It follows that the volume of the can increased by:
𝑉1 = 𝜋𝑟2ℎ
𝑉2 = 𝜋 1.30𝑟 2
ℎ
𝑉2
𝑉1
=
𝜋 ⋅ 1.30 ⋅ 1.30 ⋅ 𝑟2
⋅ ℎ
𝜋 ⋅ 𝑟2⋅ ℎ
= 1.30 ⋅ 1.30 = 1.69
69%

Domain and Range Problems (1 of 4)
Example 7. The entire graph of the function 𝑓 is shown
in the figure below. Write the domain and range of 𝑓 as
intervals or unions of intervals.

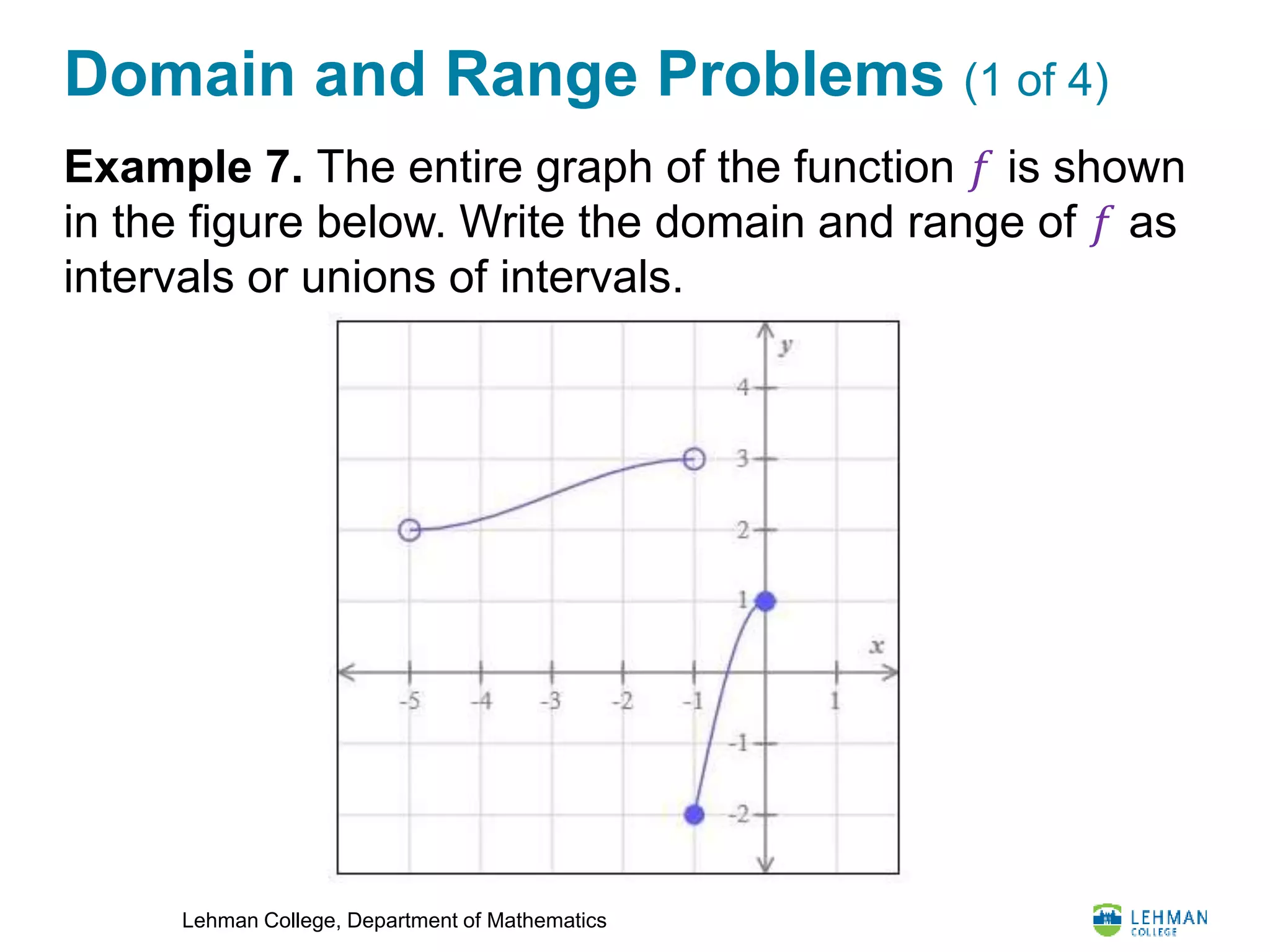
Solution. Determine the domain and range of each
piece of the graph of 𝑓.
−5, −1 ∪ [−1, 0]
= (−5, 0]
Range of 𝑓:
−2, 1 ∪ 2, 3
Domain of 𝑓:

Example 8. The entire graph of the function 𝑔 is shown
in the figure below. Write the domain and range of 𝑔 as
intervals or unions of intervals.

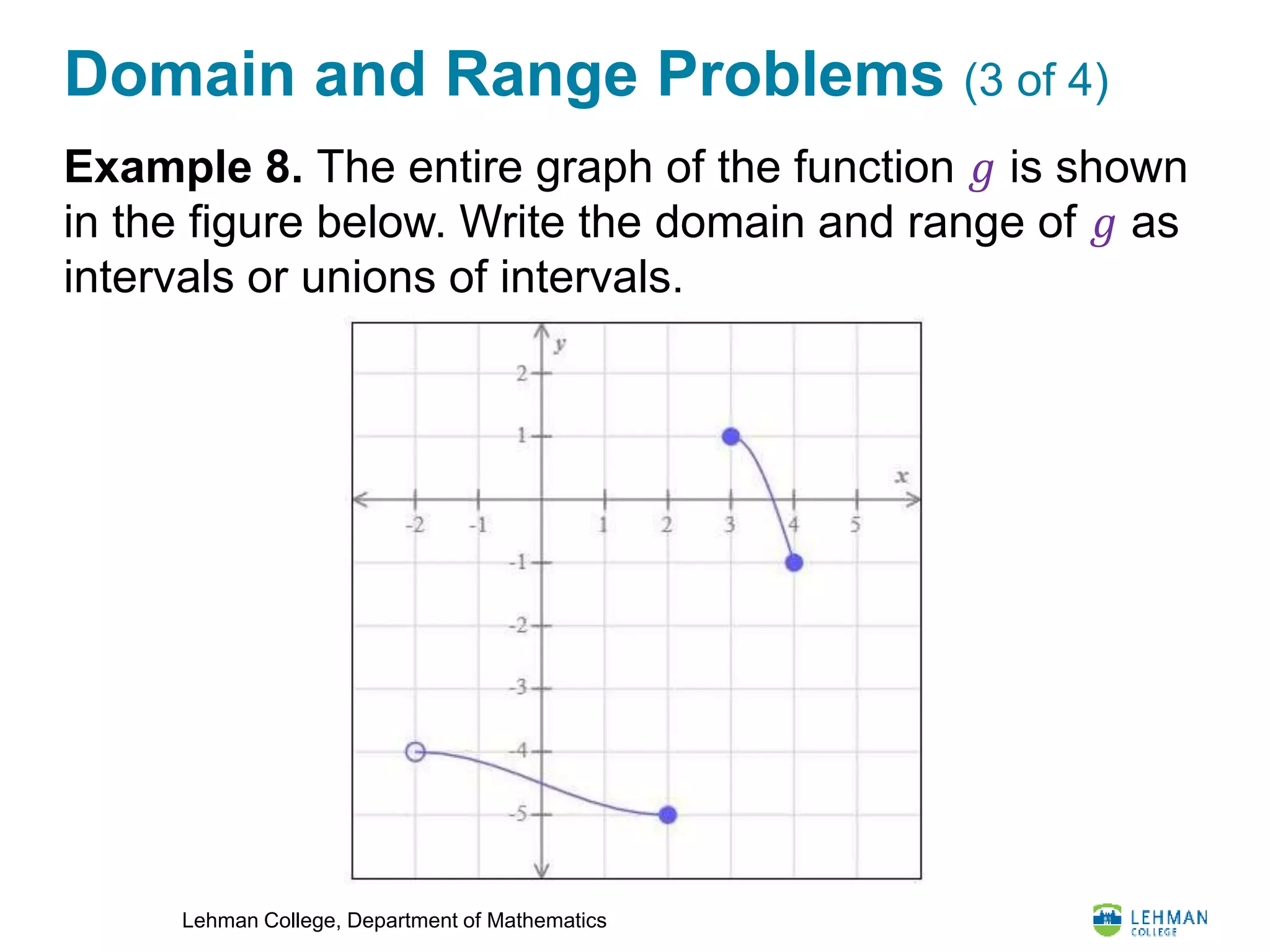
Solution. Determine the domain and range of each
piece of the graph of 𝑔.
(−2, 2] ∪ [3, 4]
Range of 𝑔:
[−5, −4) ∪ [−1, 1]
Domain of 𝑔:

Quadratic Functions (1 of 1)
Example 9. Write the quadratic function whose zeros
are 4 and −3, and whose leading coefficient is −2.
Solution. The factor theorem for polynomials states
that if 𝑎 is a zero of a polynomial, then 𝑥 − 𝑎 is a factor
of that polynomial. Let 𝑃(𝑥) be the desired quadratic.
Since 𝑃 4 = 0, then 𝑥 − 4 is a factor of 𝑃(𝑥). Similarly,
since 𝑃 −3 = 0, then 𝑥 − −3 = 𝑥 + 3 is a factor of
𝑃(𝑥). It follows that:
𝑃 𝑥 = −2(𝑥 − 4)(𝑥 + 3)
= −2(𝑥2 + 3𝑥 − 4𝑥 − 12)
= −2(𝑥2
− 𝑥 − 12)
= −2𝑥2
+ 2𝑥 + 24

Domain of Rational Functions (1 of 2)
A rational function is a function of the form:
Where 𝑝(𝑥) and 𝑞(𝑥) are polynomials. The values of 𝑥
that are not in the domain of 𝑓 are obtained by solving:
Example 8. Find the values of 𝑥 that are not in the
domain of 𝑓, defined by:
Solution. Set the denominator of the rational function
equal to zero and solve the resulting equation.
𝑝 𝑥
𝑞(𝑥)
𝑞 𝑥 = 0
𝑓 𝑥 =
𝑥 + 3
𝑥2 − 3𝑥 − 18

Domain of Rational Functions (2 of 2)
Solution (cont’d). Set the denominator of the rational
function equal to zero and solve the resulting equation.
Therefore, 𝑥 − 6 = 0 or 𝑥 + 3 = 0, so 𝑥 = 6 or 𝑥 = −3
are excluded from the domain of the rational function.
It follows that the domain of the rational function is given
by:
or
That is: all reals except −3 and 6.
𝑥2
− 3𝑥 − 18 = 0
𝑥 − 6 𝑥 + 3 = 0
ℝ − {−3, 6}
ℝ ∖ {−3, 6}

Lesson 15: Geometry

More Related Content

What's hot

Similar to Lesson 15: Geometry

More from Kevin Johnson

Recently uploaded

Lesson 15: Geometry