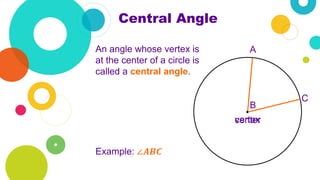
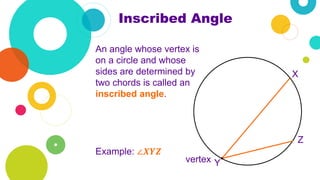
The document outlines a geometry curriculum focused on circles, covering essential concepts such as radius, diameter, and angles. It includes several activities for students, such as drawing circles, naming parts, and solving true/false statements about circle properties. Additional exercises involve using a compass to explore circle characteristics and relationships among its parts.

1. Mathematics 7
3rd Quarter: Geometry
Circle and
Its Parts
MR. CARLO JUSTINO J. LUNA
Malabanias Integrated School
Angeles City

2. CONTENT STANDARD
The learner demonstrates
understanding of key
concepts of geometry of
shapes and sizes, and
geometric relationships.

3. PERFORMANCE STANDARD
The learner is able to create
models of plane figures and
formulate and solve
accurately authentic
problems involving sides and
angles of a polygon.

4. LEARNING
COMPETENCY
The learner
illustrates a circle
and the terms
related to it:
radius, diameter,
center, arc,
chord, tangent,
secant, central
angle, and
inscribed angle.
M7GE-IIIg-1

5. ACTIVITY
Directions:
1. Draw a point
somewhere in
the middle of a
sheet of paper.

6. ACTIVITY
Directions:
2. Now, using a
ruler, mark 20
other points
that are 5 cm
from the first
point.

7. ACTIVITY
Directions:
3. Compare
your work with
that of your
seatmates.
What shape do
you recognize?

9. Naming the parts of a circle

10. Drag and
drop the
words on
the
illustration.

11. Central Angle
An angle whose vertex is
at the center of a circle is
called a central angle.
Example: ∠𝑨𝑩𝑪
vertex
A
B
C
center

12. Inscribed Angle
An angle whose vertex is
on a circle and whose
sides are determined by
two chords is called an
inscribed angle.
Example: ∠𝑿𝒀𝒁
vertex
X
Y
Z

13. ACTIVITY
A. Determine whether each statement
is true or false.
1. Two radii always have the same
length.
2. Two chords always have the same
length.
3. All chords are diameters.
4. All diameters are chords.
5. All chords intersect at one point.
6. A radius is not a chord.
7. All diameters intersect at one point

14. ACTIVITY
B. Illustrate the parts of the given
circle:
1. Center: 𝑂
2. Radii: 𝑂𝐴, 𝑂𝐸
3. Diameter: 𝐵𝐷
4. Chord: 𝐵𝐶
5. Tangent: 𝐷𝐹
6. Secant: 𝐴𝐷
7. Central Angles: ∠𝐴𝑂𝐵, ∠𝐷𝑂𝐸
8. Inscribed Angle: ∠𝐶𝐵𝐸

15. ADDITIONAL ACTIVITIES
Using a compass, draw a circle whose radius is 5cm.
1. What is the length of the diameter of the circle?
2. How many sectors of 90° will fit inside the circle?
3. Draw five radii inside your circle that are equally spaced out
around the circumference. Join up the ends of the radii to
create a shape inside your circle.
4. What is the name of the shape that you have created inside
your circle?
5. How long are the chords that are joining the radii together?
6. How big is the angle of each sector?
7. If you did the same as above with sectors of 45°, what
shape would you create inside your circle?

16. THANKS!
MR. CARLO JUSTINO J. LUNA
Malabanias Integrated School
Angeles City

17. Credits
Special thanks to all the people who
made and released these awesome
resources for free:
◎Presentation template by
SlidesCarnival
◎Naming Activity by BoardWorks
◎Shockwave Flash by Teachade