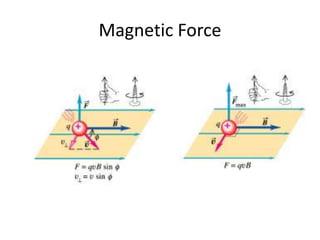
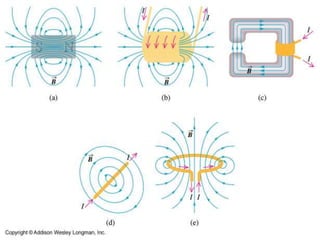
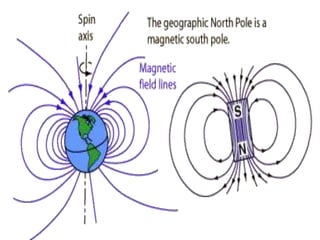
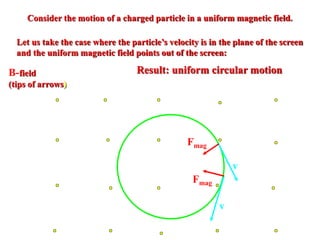
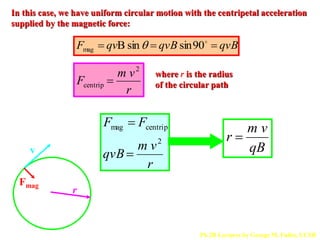
The magnetic field B is defined by the Lorentz force law, which states that the magnetic force Fmag on a particle with charge q and velocity v is equal to q crossed with the product of v and B. This causes the particle to move in a circular path, with the magnetic force providing the necessary centripetal force. Magnetic field lines are used to represent magnetic fields graphically, with the direction of the force on a charged particle given by the right-hand rule where it is perpendicular to both the velocity and magnetic field vectors.

1. Magnetism
Magnetic Force

2. Magnetic Force
• The magnetic field is defined from the Lorentz
Force Law,
 BvqEqF



3. Magnetic Force
• The magnetic field is defined from the Lorentz
Force Law,
• Specifically, for a particle with charge q
moving through a field B with a velocity v,
• That is q times the cross product of v and B.
 BvqEqF


 BvqF



4. Magnetic Force
• The cross product may be rewritten so that,
• The angle is measured from the direction of
the velocity to the magnetic field .
sinvBqF 


v

B

v x B
B
v


5. Magnetic Force

6. Magnetic Force
• The diagrams show the direction of the force
acting on a positive charge.
• The force acting on a negative charge is in the
opposite direction.
+
-
v
F
F
B
B
v

7. Magnetic Force
• The direction of the force F acting on a
charged particle moving with velocity v
through a magnetic field B is always
perpendicular to v and B.

8. Magnetic Force
• The SI unit for B is the tesla (T) newton per
coulomb-meter per second and follows from
the before mentioned equation .
• 1 tesla = 1 N/(Cm/s)
B
vq
F

sin


9. Magnetic Field Lines
• Magnetic field lines are used to represent the
magnetic field, similar to electric field lines to
represent the electric field.
• The magnetic field for various magnets are
shown on the next slide.

12. We can define the magnetic field B (a vector quantity) at a point by the vector
force Fmag at that point experienced by a particle with charge q and velocity v:
Lorentz Force Law

Fmag  q v  B
If there is also an electric field E at this point, then in addition
to the above magnetic force, there will be an electric force Felec=qE
and the total force Ftot on the charge will be
Ftot = Felec  Fmag  q E  q v B
 q E  v B 
Ph 2B Lectures by George M. Fuller, UCSD

13. The (vector) magnetic force on the charge q
at a particular point in space depends on the (vector) velocity of the charge and
on the (vector) magnetic field at this point:

Fmag  q v  B
The magnitude of this force is
Fmag  Fmag  q v B sin  qvB sin
where  is the angle between the velocity
vector v and the magnetic field vector B at this
point in space
Ph 2B Lectures by George M. Fuller, UCSD

14. What about the direction of the force?
Since the force is given by the vector cross product of velocity and
magnetic field, it is orthogonal to both of these. That is, the force vector will
be perpendicular to the plane defined by the velocity and magnetic field
vectors.
Fmag
v
B

Fmag  q v  B
Fmag  Fmag  q v B sin  qvB sin

Ph 2B Lectures by George M. Fuller, UCSD

15. Consider the motion of a charged particle in a uniform magnetic field.
Let us take the case where the particle’s velocity is in the plane of the screen
and the uniform magnetic field points out of the screen:
B-field
(tips of arrows)
v
Fmag
v
Fmag
Result: uniform circular motion

16. In this case, we have uniform circular motion with the centripetal acceleration
supplied by the magnetic force:

Fmag  qvB sin  qvB sin90  qvB

Fcentrip 
m v2
r
v
Fmag
r
where r is the radius
of the circular path

Fmag  Fcentrip
qvB
m v2
r

r 
m v
qB
Ph 2B Lectures by George M. Fuller, UCSD