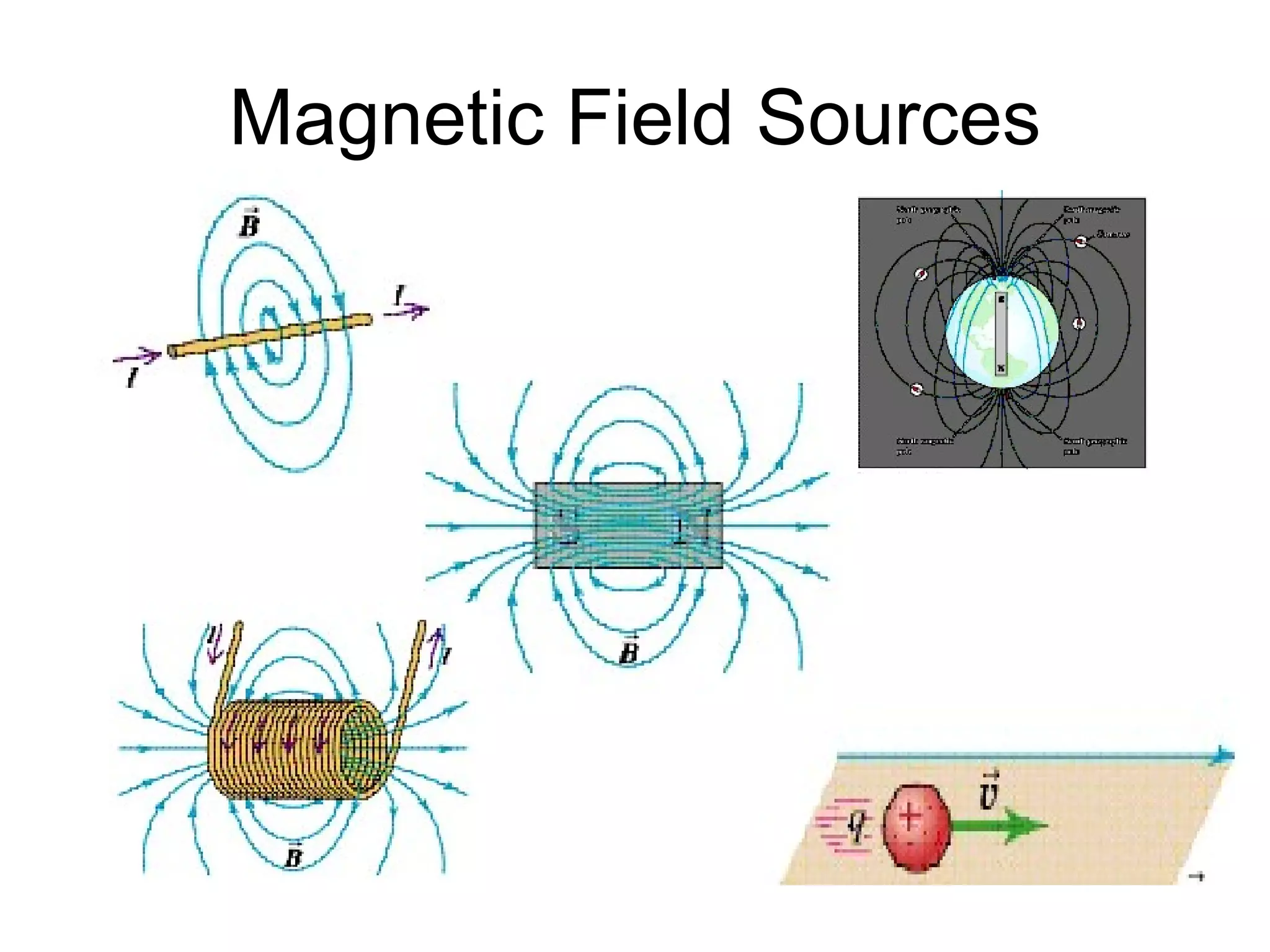
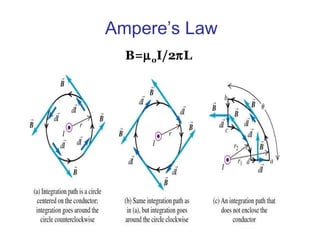
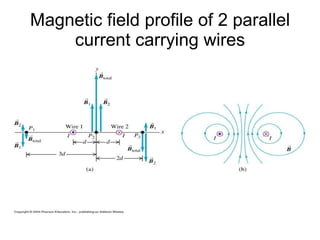
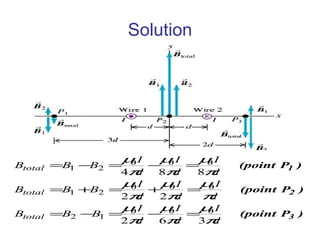
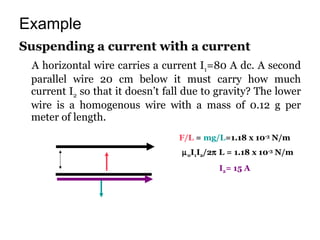
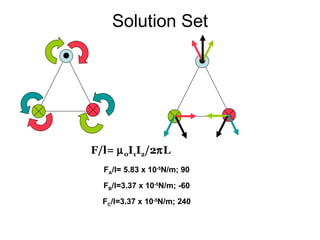
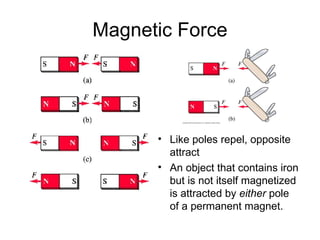
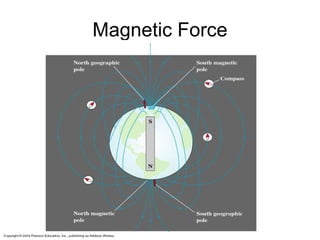
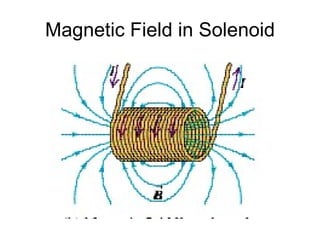
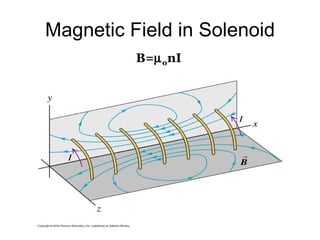
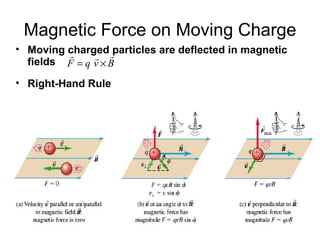
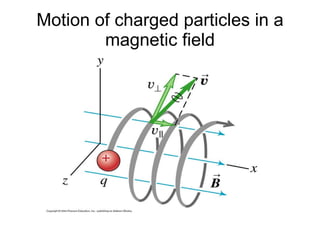
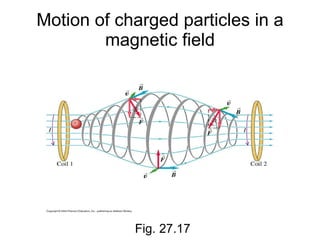
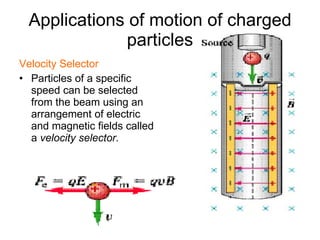
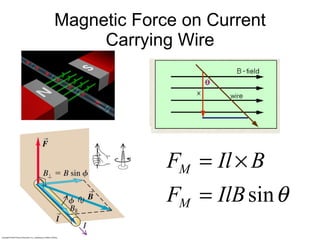
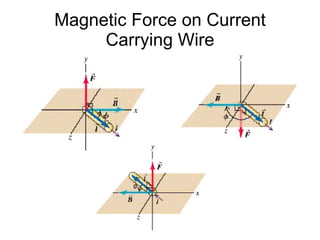
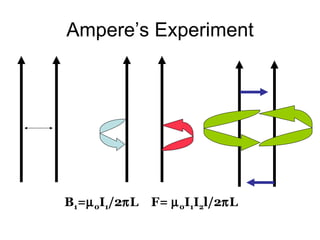
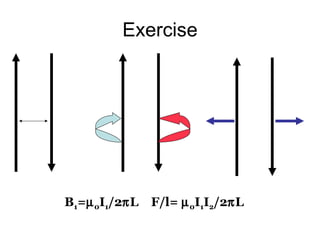
1. Magnetic fields are force fields that exert non-contact forces on other magnets or current-carrying conductors. They are generated by moving charges and currents. 2. Magnetic field lines emanate from the north pole of a magnet and loop back to the south pole. Opposite magnetic poles attract, while like poles repel one another. 3. A magnetic force is exerted on any moving charge or current in a magnetic field. This force is perpendicular to both the magnetic field and the velocity of the charge or current.

1. Magnetic Field Sources

3. Magnetic field lines

5. Magnetic Force

9. Grip and Hand Rules Out of the Page In to the Page

11. Magnetic Force on Moving Charge The magnetic force is always perpendicular to v ; a particle moving under the action of a magnetic field alone moves with a constant speed.

12. Motion of charged particles in a magnetic field

13. Motion of charged particles in a magnetic field Fig. 27.18

14. Motion of charged particles in a magnetic field Fig. 27.17

16. Magnetic Force on Current Carrying Wire

17. Magnetic Force on Current Carrying Wire

19. Ampere’s Law B=  0 I/2  L

20. Magnetic field profile of 2 parallel current carrying wires

21. Solution

22. Magnetic Field in Solenoid

23. Magnetic Field in Solenoid B=  0 nI

24. Ampere’s Experiment B 1 =  0 I 1 /2  L F=  0 I 1 I 2 l/2  L

25. Exercise B 1 =  0 I 1 /2  L F/l=  0 I 1 I 2 /2  L

28. Solution Set F/l=  0 I 1 I 2 /2  L F A /l= 5.83 x 10 -5 N/m; 90 F B /l=3.37 x 10 -5 N/m; -60 F C /l=3.37 x 10 -5 N/m; 240