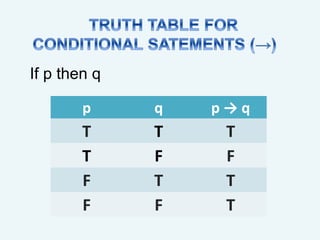
This document discusses propositional logic and truth tables. It defines primitive and compound propositions. Logical connectives like negation, disjunction, and conjunction are explained. Propositional variables are used to represent statements that can be true or false. Truth tables list all possible combinations of true and false values for propositional variables and determine the truth value of compound statements formed from logical connectives. The number of rows in a truth table is determined by 2 to the power of the number of propositional variables. Several examples of truth tables are given for logical connectives like negation, disjunction, conjunction, implication, and biconditional.

1. By D .Nayanathara (BSc in MIS)By D .Nayanathara (BSc in MIS)

2. • SENTENCE THAT IS ETHIER TRUE (T)OR FALSE(F)
Ex –
• 3 + 5 = 8 : Proposition
• 9 - 2 = 5 : Proposition
• a < b : Not a Proposition
• Who can speak French: Not a Proposition

3. • PRIMITIVE PROPOSITION - Can not be
broken down in to simple proposition.
• COMPOSITE OR COMPOUND
PROPOSITION – Can be broken down in
to two or more primitive propositions.
Ex – 2+3 = 5 and 1+7 = 4
Birds can fly or Today is hot.

4. Name Symbol Operation
Negative not ~
Disjunction or ˅
Conjunction and ˄

5. • Proposition variables used to describe
proposition
• Propositional Variable is variable which
either true or false
• In logic p,q,r ,.. Letters used to indicate
these variables
Ex: p indicate negative of the p̴̴̴̴

6. Truth table lists whether a statement
is true or false.
Truth Tables defined the logical
connectives of the compound
statements(compound propositions).
The sentences built out of propositions
and logical connectives are also
propositions. They have truth values.

7. • Column must be allocated for each
proposition variables in the compound
statement and for the final compound
proposition.
• Truth Tables should contain all the
possible combinations (truth values) of T
and F values for all proposition
variables.

8. • Number of rows in truth table
indicates by 2n
where n is the
number of propositions.
Ex : Birds can fly or Today is hot.
1. Birds can fly
2. Today is hot
There are two propositions in the
compound statement : n = 2
So, Number of rows (combinations) = 22
= 4

9. p p̴̴̴̴
T F
F T

10. p q p v q
T T T
T F T
F T T
F F F

11. p q p q˄
T T T
T F F
F T F
F F F

12. p pv p̴̴̴̴
T T
F T
Ex :pv( p̴̴̴̴ ˄q)
Formula which is always True (or T )

13. p q p q˄ ~(p q)˄ pv~(p q)˄
T T T F T
T F F T T
F T F T T
F F F T T
Ex : pv( p̴̴̴̴ ˄q)

14. p p p˄ ̴̴̴̴
T F
F F
Ex: (pv (not p))  ((p (not p))˄
(p q) not(pvq)˄ ˄
Formula which is always False (or F)

15. p q p q˄ p v q ~(p v q) (p q) ~(p v q)˄ ˄
T T T T F F
T F F T F F
F T F T F F
F F F F T F
Ex : (p˄q) ˄~(pvq)

16. p q p → q
T T T
T F F
F T T
F F T
If p then q

17. p q p ↔ q
T T T
T F F
F T F
F F T
p if and only if q (iff)