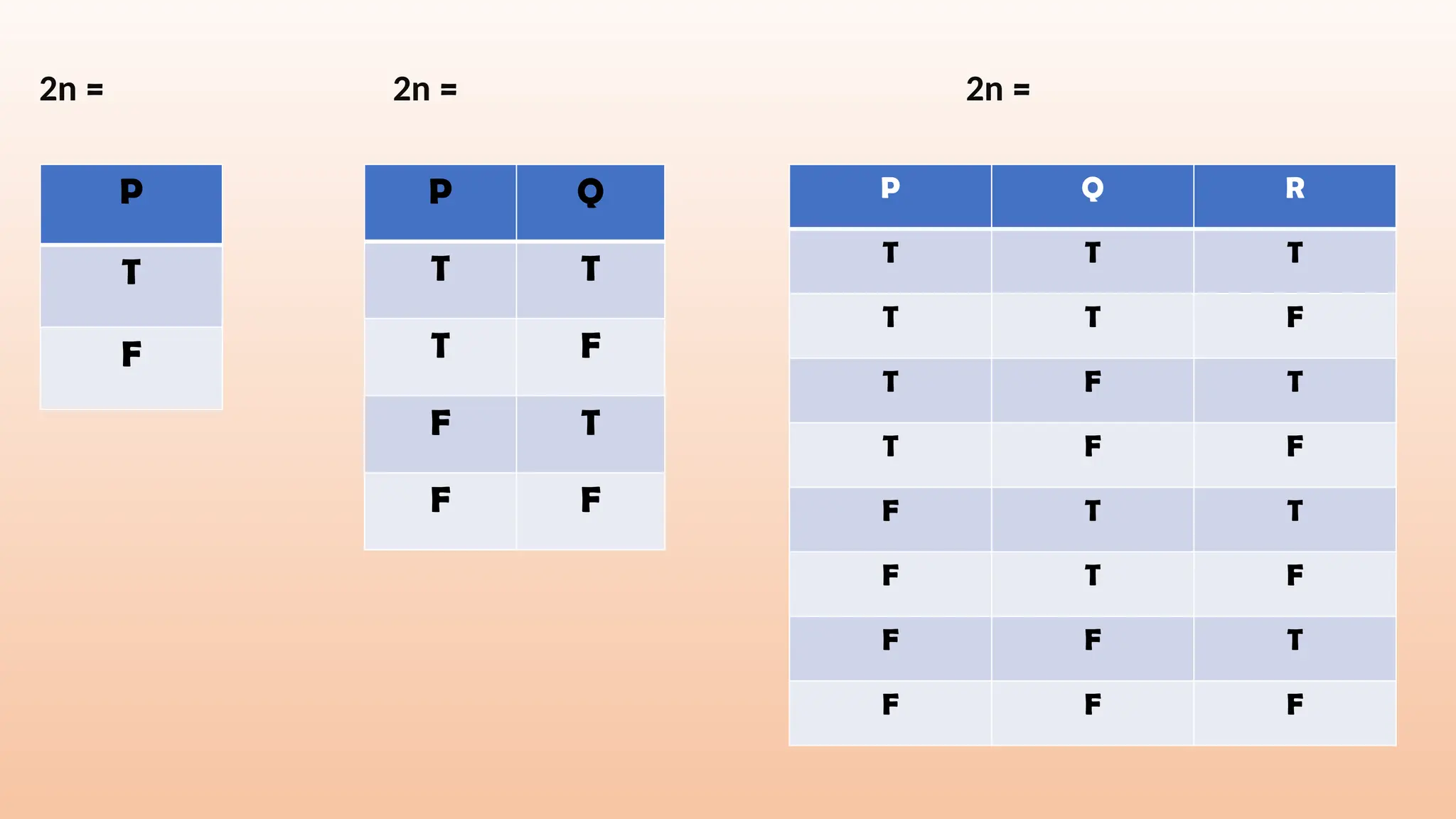
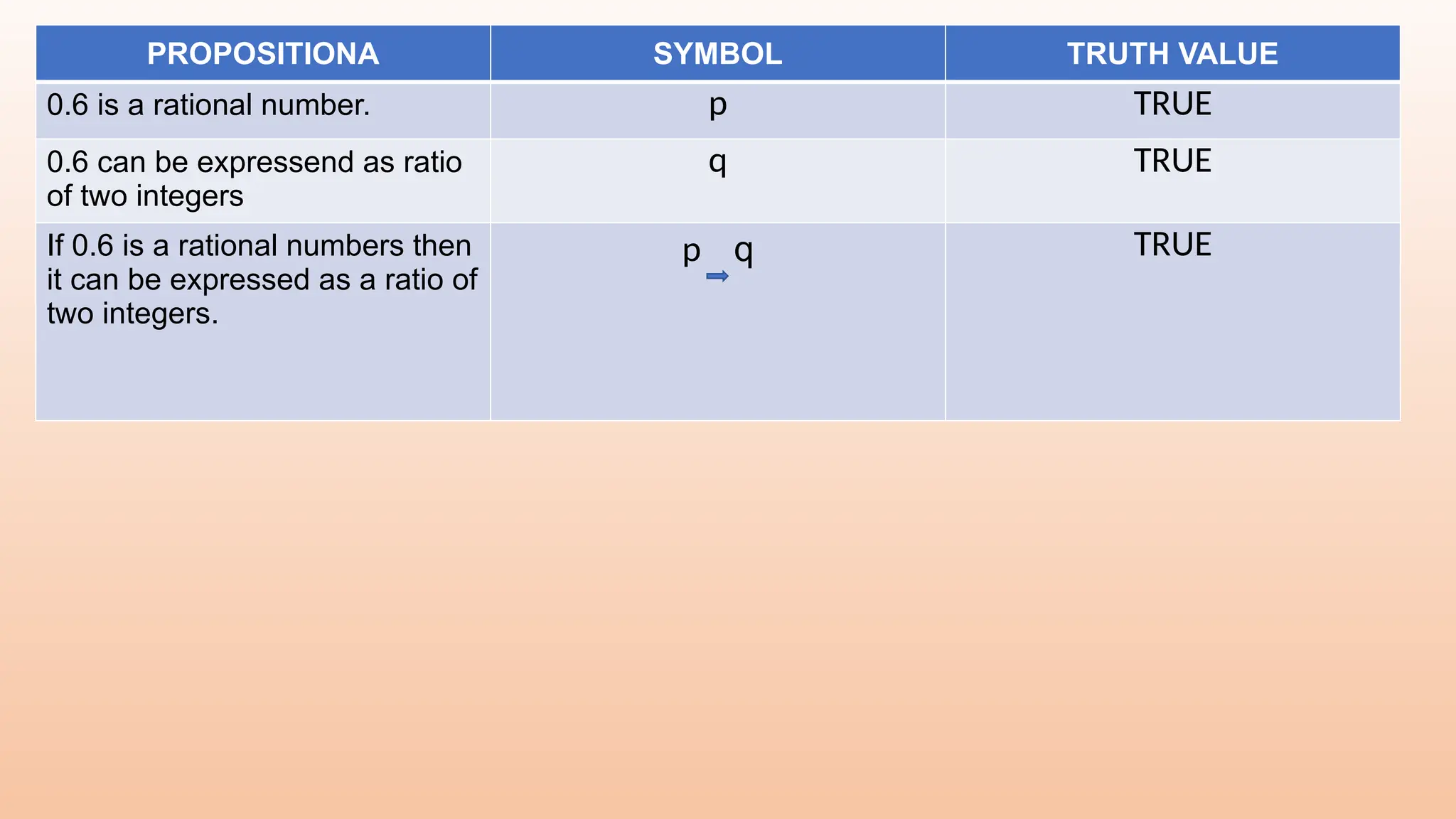
The document discusses various logical statements and their classifications, including statements, questions, commands, and opinions, highlighting the structure of simple declarative sentences. It covers concepts such as truth tables, negation, conjunction, disjunction, and implications, as well as the validity of arguments using symbolic logic and Euler diagrams. The text emphasizes the process for determining argument validity and the distinction between valid and invalid arguments.

1. LOGIC STATEMENT QUANTIFIERS

2. Every language contains different
types of sentences, such as statement,
questions, and commands. For instance :
Is the best today? – is a question
Go get the newspaper – is a command
This is a nice bar – is an opinion
FSM Student’s are beautiful and
handsome – is a statement of fact

3. S
T
A
T
E
M
E
N
T
- A simple
declarative sentence
that is either true or
false but not both
true and false

4. A simple declarative sentence has a
simple sentences structure, consisting
of a subject and predicate.
Examples:
• My dog is sick
• It is a nice day

5. Identify statement;
Determine wheater each sentences is a
Stament
1. Florida is a state in the United State
2. How are you?
3. x+1= 5

6. T
R
U
T
H
T
A
B
L
E
&
T
A
U
T
O
L
O
G
I
E
S
Is a mathematical table use to determine
if a compound statement is true or false
in the truth table each statement is typically
represented by letter or variable like P, Q, or R
and each statement also have a corresponding
column to the truth table

7. 2n = 2n = 2n =
P
T
F
P Q
T T
T F
F T
F F
P Q R
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F

8. NEGATION
A negation can be constructed by changing is not, can by
cannot, do by do not, and other revisions such as those
mentioned.
PROPOSITION SYMBOLS TRUTH VALUE
Even number are multiple of 2. p True
Even numbers are not multiples
by 2
~p False
CONJUCTION
A conjuction can be constructed by combining two
simple propositions using the connective “and”

9. PROPOSITION SYMBOLS TRUTH VALUE
2 is a prime number. p True
2 is an even number. q True
CONSTRUCTION 1
2 is a prime number and 2 is an
even number
CONSTRUCTION 2
2 is both a prime number and an
even number
p^q True
DISJUCTION
A disjuction can be constructed by combining two simple
proposition using the connective “or”

10. PROPOSITIONA SYMBOL TRUTH VALUE
10 is a multiple of 5. p TRUE
15 is a multiple of 5. q TRUE
CONSTRUCTION 1
10 is a multiple of 5 or 15 is a
multiple of 5
CONTRUCTIONAL 2
Either 10 or 15 is multiple of 5
p^q TRUE
IMPLICATION
An implication can be constructed by combining two simple
propositions becomes the “if-statement” and other becomes the “ then-
statement.”

11. PROPOSITIONA SYMBOL TRUTH VALUE
0.6 is a rational number. p TRUE
0.6 can be expressend as ratio
of two integers
q TRUE
If 0.6 is a rational numbers then
it can be expressed as a ratio of
two integers.
p q TRUE

12. CONDITIONAL, BICONDITIONAL
AND RELATED STATEMENT

13. The conditional p→q may also be reas as “p implies q”. The
proposition p is called hypothesis, while the proposition q called the
conclusion.
(T ＋ F =F always !)
TRUTH TABLE FOR AN IMPLICATION
P q p→q
T T T
T F F
F T T
F F T
The conditional of the propositions p and q is donated by
p→q:(If p, then q)and is defined through its truth table

14. p q r p→r
T T T T
T T F F
T F T T
T F F F
F T T T
F T F T
F F T T
F F F T
The biconditional of proposition p and q is
denoted by p↔q (p if and only q) and is defined
through its truth table.

15. p q p q
↔
T T T
T F F
F T F
F F T
The proposition may also be written as “p if q”. The
propositions p and q are the components of the
biconditional.
(T ＋ T AND F ＋ F are always true!)

16. p q r p→r
T T T T
T T F F
T F T T
T F F F
F T T T
F T F T
F F T T
F F F T

17. SYMBOLIC ARGUMENTS

18. Symbolic logic is mainly a study of arguments and since argument
is made up of propositions, there is a need to determine the
truthfulness or falsity of these propositions in order to know the
validity or invalidity of an argument.
An argument is a collection of propositions where it is
claimed that one of the propositions called conclusion
follows from the other propositions called premises of the
argument is denoted by P1, P2, ....,Pn/Q.

19. ILLUSTRATION:
• If a man is
bachelor, then he is
unhappy.
• If he is unhappy,
then he dies young.
• So, bachelor dies
young
Premise 1 ( P1 )
Premise 2 (P2 )
Conclusion ( / Q)

20. STEPS IN DETERMINING THE VALIDITY OF AN ARGUMENT
 Write the argument in a symbolic form.
 construct a truth table showing the truth table of the premises and the truth
value of the conclustion
 if the conclustion is true in every row of the truth table in whichall the premises
are true, then the argument is valid.
 if the conclusion is false in any row in whichj premises are true, then the
argument is invalid.
An argument is valid if the conclustion is true whenever all the
premises are assumed to be true. Otherwise, an argument is invalid if
at least one of the conclusion is false, It can be written in symbolic
form to construct the triuth table and its validity can be verified using
truth table

21. EXAMPLE :
If a man is a bachelor, then he is unhappy. if he is unhappy, then he
dies young. So, bachelor dies young.
LET :
B= “ Man is bachelor.”
U= “ Man is unhappy.”
Y= “ Man dies young.”
The given arguments can be express as
• If a man is bachelor then he is unhappy. -- b → u ( P1 )
• If he is unhappy, then he dies young. -- u → y ( P2 )
• So bachelor dies young. --/ b → y ( Q)

22. ARGUMENTS AND EULER DIAGRAMS

23. In the preceding lesson, truth tables are used as a tool in determining the validity of an arguments.
Now, the use of Euler diagrams will be introduced in determining the validity of such arguments.
The constructionof Euler diagrams will be taught along the course of discussion.
In this lesson, arguments that are composed of set 2 or more premises and conclusion are
considered.
Such example is the one written next
In an Euler Diagram, a circle is used to represent a set of objects. In the below example, mammal is
a smaller set inside the set of vertebrates, Figure 7.5.1 showa this relationship. Note that, the cow.
Since the cross mark is also inside the set of vertebrates, the arguments is valid
Figure 7.5.1
Mammals
×
Vertebrates
All mammals are vertabrates
Cow is a mammal.
Therefore, cow is a
vertabrate

24. Not all arguments are valid of course, there are some that are not
invalid. If an arguments is nor valid, it called an Invalid argument.
How can one know that an argument is invalid? Study the next
argument.
× ?
MONKEY
X?
Animals that eat Banana
All monkey eat banana.
Marc eat banana
Therefore, Marc is a monkey
FIGURE; 7.5.2

25. The Euler diagram for this argument is show in Figure 7.5.2,
Note that premise Marc eats banana suggests that the cross
mark can be inside the set of monkeys, or outside it. If is
inside, the argument is valid; If it is inside, If it is outside, the
arguments is invalid. This uncertainly led logicians to junk this
argument as invalid
An argument that is invalid may have a conclusion that may or
may not be true. It is not clear whether Marc is name of a
monkey. In short, an invalid arguments does not mean that our
conclusion is false and a valid argument Implies a true
conclusion. Validity only depends on the set of premises that
are considered true.