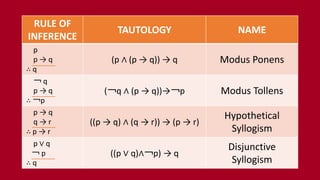
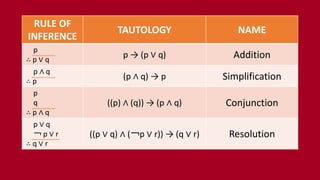
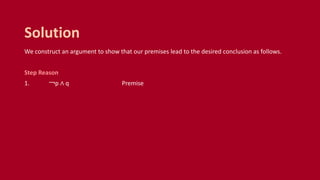
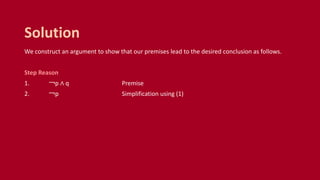
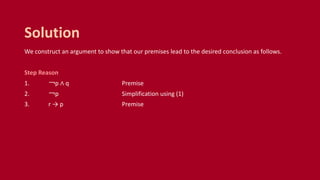
This document summarizes rules of inference in propositional logic. It defines an argument as a sequence of propositions where all but the final proposition are premises and the final is the conclusion. An argument is valid if the truth of the premises implies the truth of the conclusion. Various rules of inference are provided, including modus ponens, modus tollens, and hypothetical syllogism. Examples are given of identifying and applying different rules of inference to determine the validity of arguments.

1. Rules of Inference
Lecture 4, CMSC 56
Allyn Joy D. Calcaben

2. Templates for constructing valid arguments
Our basic tools for establishing the truth of statements
Fallacies
common forms of incorrect reasoning which lead to
invalid arguments
Rules of Inference

3. An argument in propositional logic is a sequence of
propositions.
All but the final proposition in the argument are called
premises and the final proposition is called the conclusion.
An argument is valid if the truth of all its premises
implies that the conclusion is true.
Rules of Inference

4. An argument form in propositional logic is a sequence of
compound propositions involving propositional variables.
An argument form is valid no matter which particular
propositions are substituted for the propositional variables in
its premises, the conclusion is true if the premises are all true.
Rules of Inference

5. Valid Arguments
in Propositional Logic

6. “If you have a current password,
then you can log onto the network.”
Example

7. “If you have a current password,
then you can log onto the network.”
“You have a current password.”
Example

8. “If you have a current password,
then you can log onto the network.”
“You have a current password.”
Therefore,
Example

9. “If you have a current password,
then you can log onto the network.”
“You have a current password.”
Therefore,
“You can log onto the network.”
Example

10. Argument form:
p → q
p
∴ q
where ∴ is the symbol that denotes “therefore.”
Example

11. Argument form:
p → q
p
∴ q
where ∴ is the symbol that denotes “therefore.”
Example
PREMISES
CONCLUSION

12. To determine whether this is a valid argument,
determine whether the conclusion “You can log onto the
network” is true when the premises “If you have a current
password, then you can log onto the network” and “You have
a current password” are both true.
Example

13. “If you have a current password, then you can log onto the network.”
“You have a current password.”
∴ “ You can log onto the network.”
Example

14. RULE OF
INFERENCE
TAUTOLOGY NAME
p
p → q
∴ q
(p ∧ (p → q)) → q Modus Ponens
￢ q
p → q
∴ ￢p
(￢q ∧ (p → q))→￢p Modus Tollens
p → q
q → r
∴ p → r
((p → q) ∧ (q → r)) → (p → r)
Hypothetical
Syllogism
p ∨ q
￢ p
∴ q
((p ∨ q)∧￢p) → q
Disjunctive
Syllogism

15. RULE OF
INFERENCE
TAUTOLOGY NAME
p
∴ p ∨ q
p → (p ∨ q) Addition
p ∧ q
∴ p
(p ∧ q) → p Simplification
p
q
∴ p ∧ q
((p) ∧ (q)) → (p ∧ q) Conjunction
p ∨ q
￢ p ∨ r
∴ q ∨ r
((p ∨ q) ∧ (￢p ∨ r)) → (q ∨ r) Resolution

16. State which rule of inference is the basis of the following
argument:
“ It is below freezing now.
Therefore, it is either below freezing or raining now. ”
Example

17. “ It is below freezing now.
Therefore, it is either below freezing or raining now. ”
Let p be the proposition “It is below freezing now. ”
and q be the proposition “It is raining now. ”
Solution

18. “ It is below freezing now.
Therefore, it is either below freezing or raining now. ”
Let p be the proposition “It is below freezing now. ”
and q be the proposition “It is raining now. ”
Then this argument is of the form
Solution

19. “ It is below freezing now.
Therefore, it is either below freezing or raining now. ”
Let p be the proposition “It is below freezing now. ”
and q be the proposition “It is raining now. ”
Then this argument is of the form
p
∴ p V q
Solution

20. “ It is below freezing now.
Therefore, it is either below freezing or raining now. ”
Let p be the proposition “It is below freezing now. ”
and q be the proposition “It is raining now. ”
Then this argument is of the form
p
∴ p V q
Solution
This is an argument that
uses the addition rule

21. State which rule of inference is the basis of the following
argument:
“ It is below freezing and raining now.
Therefore, it is below freezing now. ”
Example

22. “ It is below freezing and raining now.
Therefore, it is below freezing now. ”
Let p be the proposition “It is below freezing now. ”
and q be the proposition “It is raining now. ”
Solution

23. “ It is below freezing and raining now.
Therefore, it is below freezing now. ”
Let p be the proposition “It is below freezing now. ”
and q be the proposition “It is raining now. ”
Then this argument is of the form
p ∧ q
∴ p
Solution

24. “ It is below freezing and raining now.
Therefore, it is below freezing now. ”
Let p be the proposition “It is below freezing now. ”
and q be the proposition “It is raining now. ”
Then this argument is of the form
p ∧ q
∴ p
Solution
This is an argument that
uses the simplification rule

25. State which rule of inference is used in the argument:
“ If it rains today, then we will not have a barbeque today.
If we do not have a barbeque today, then we will have a
barbecue tomorrow.
Therefore, if it rains today, then we will have a barbecue
tomorrow. ”
Example

26. Let p be the proposition “It is raining today. ”
let q be the proposition “We will not have a barbecue today.”
and r be the proposition “We will have a barbecue tomorrow.”
Solution

27. Let p be the proposition “It is raining today. ”
let q be the proposition “We will not have a barbecue today.”
and r be the proposition “We will have a barbecue tomorrow.”
Then the argument is of the given form:
p → q
q → r
∴ p → r
Solution

28. Let p be the proposition “It is raining today. ”
let q be the proposition “We will not have a barbecue today.”
and r be the proposition “We will have a barbecue tomorrow.”
Then the argument is of the given form:
p → q
q → r
∴ p → r
Solution
This argument is a
hypothetical syllogism

29. Definition 2
A formal proof of a conclusion q given hypotheses p1, p2, . . . ,
pn is a sequence of steps, each of which applies some
inference rule to hypotheses or previously proven statements
(antecedents) to yield a new true statement (the consequent).
Formal Proof

30. Definition 2
A formal proof of a conclusion q given hypotheses p1, p2, . . . ,
pn is a sequence of steps, each of which applies some
inference rule to hypotheses or previously proven statements
(antecedents) to yield a new true statement (the consequent).
A formal proof demonstrates that if the premises are true,
then the conclusion is true.
Formal Proof

31. Using Rules of Inference
to Build Arguments

32. Show that the premises:
“It is not sunny this afternoon and it is colder than yesterday,”
“We will go swimming only if it is sunny,”
“If we do not go swimming, then we will take a canoe trip,”
and “If we take a canoe trip, then we will be home by sunset”
lead to the conclusion “We will be home by sunset.”
Example

33. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
Solution

34. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“It is not sunny this afternoon and it is colder than yesterday”
Solution

35. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“It is not sunny this afternoon and it is colder than yesterday”
￢p ∧ q
Solution

36. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“We will go swimming only if it is sunny.”
Solution

37. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“We will go swimming only if it is sunny.”
r → p
Solution

38. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“If we do not go swimming, then we will take a canoe trip.”
Solution

39. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“If we do not go swimming, then we will take a canoe trip.”
￢r → s
Solution

40. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“If we take a canoe trip, then we will be home by sunset.”
Solution

41. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
“If we take a canoe trip, then we will be home by sunset.”
s → t
Solution

42. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
Conclusion: “We will be home by sunset.”
Solution

43. Let p be the proposition “It is sunny this afternoon,”
q the proposition “It is colder than yesterday,”
r the proposition “We will go swimming,”
s the proposition “We will take a canoe trip,”
and t the proposition “We will be home by sunset.”
Conclusion: “We will be home by sunset.”
t
Solution

44. The premises become
￢p ∧ q
r → p
￢r → s
s → t
The conclusion is simply t
Solution

45. The premises become
￢p ∧ q
r → p
￢r → s
s → t
The conclusion is simply t
We need to give a valid argument with premises ￢p ∧ q, r → p,
￢r → s, and s → t and conclusion t .
Solution

46. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
Solution

47. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
2. ￢p Simplification using (1)
Solution

48. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
2. ￢p Simplification using (1)
3. r → p Premise
Solution

49. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
2. ￢p Simplification using (1)
3. r → p Premise
4. ￢r Modus tollens using (2) and (3)
Solution

50. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
2. ￢p Simplification using (1)
3. r → p Premise
4. ￢r Modus tollens using (2) and (3)
5. ￢r → s Premise
Solution

51. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
2. ￢p Simplification using (1)
3. r → p Premise
4. ￢r Modus tollens using (2) and (3)
5. ￢r → s Premise
6. s Modus ponens using (4) and (5)
Solution

52. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
2. ￢p Simplification using (1)
3. r → p Premise
4. ￢r Modus tollens using (2) and (3)
5. ￢r → s Premise
6. s Modus ponens using (4) and (5)
7. s → t Premise
Solution

53. We construct an argument to show that our premises lead to the desired conclusion as follows.
Step Reason
1. ￢p ∧ q Premise
2. ￢p Simplification using (1)
3. r → p Premise
4. ￢r Modus tollens using (2) and (3)
5. ￢r → s Premise
6. s Modus ponens using (4) and (5)
7. s → t Premise
8. t Modus ponens using (6) and (7)
Solution

54. Show that the premises:
“If you send me an e-mail message, then I will finish writing
the program,”
“If you do not send me an e-mail message, then I will go to
sleep early,” and
“If I go to sleep early, then I will wake up feeling refreshed”
lead to the conclusion “If I do not finish writing the program,
then I will wake up feeling refreshed.”
Example

55. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
Solution

56. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
“If you send me an e-mail message,
then I will finish writing the program”
Solution

57. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
“If you send me an e-mail message,
then I will finish writing the program”
p → q
Solution

58. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
“If you do not send me an e-mail message,
then I will go to sleep early”
Solution

59. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
“If you do not send me an e-mail message,
then I will go to sleep early”
￢p → r
Solution

60. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
“If I go to sleep early,
then I will wake up feeling refreshed”
Solution

61. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
“If I go to sleep early,
then I will wake up feeling refreshed”
r → s
Solution

62. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
Conclusion: “If I do not finish writing the program,
then I will wake up feeling refreshed”
Solution

63. Let p be the proposition “You send me an e-mail message,”
q the proposition “I will finish writing the program,”
r the proposition “I will go to sleep early,”
and s the proposition “I will wake up feeling refreshed.”
Conclusion: “If I do not finish writing the program,
then I will wake up feeling refreshed”
￢q → s
Solution

64. The premises are
p → q
￢ p → r
r → s
The desired conclusion is ￢ q → s
Solution

65. The premises are
p → q
￢ p → r
r → s
The desired conclusion is ￢ q → s
We need to give a valid argument with premises p → q, ￢p → r,
and r → s and conclusion ￢q → s
Solution

66. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
Solution

67. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
2. ￢p → r Premise
Solution

68. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
2. ￢p → r Premise
No possible rule of inference!
Solution

69. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
Solution

70. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
2. ￢q →￢p Contrapositive of (1)
Solution

71. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
2. ￢q →￢p Contrapositive of (1)
3. ￢p → r Premise
Solution

72. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
2. ￢q →￢p Contrapositive of (1)
3. ￢p → r Premise
4. ￢q → r Hypothetical syllogism using (2) and (3)
Solution

73. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
2. ￢q →￢p Contrapositive of (1)
3. ￢p → r Premise
4. ￢q → r Hypothetical syllogism using (2) and (3)
5. r → s Premise
Solution

74. This argument form shows that the premises lead to the desired conclusion.
Step Reason
1. p → q Premise
2. ￢q →￢p Contrapositive of (1)
3. ￢p → r Premise
4. ￢q → r Hypothetical syllogism using (2) and (3)
5. r → s Premise
6. ￢q → s Hypothetical syllogism using (4) and (5)
Solution

75. Resolution

76. A rule of inference used by many Computer programs to
automate the task of reasoning and proving theorems.
Resolution

77. A rule of inference used by many Computer programs to
automate the task of reasoning and proving theorems.
((p ∨ q) ∧ (￢p ∨ r)) → (q ∨ r)
The final disjunction in the resolution rule, q ∨ r, is called the
resolvent.
Resolution

78. Show that the premises (p ∧ q) ∨ r and r → s imply the
conclusion p ∨ s.
Example

79. Show that the premises (p ∧ q) ∨ r and r → s imply the conclusion p ∨ s.
We can rewrite the premises (p ∧ q) ∨ r as two clauses using the
Distributive laws:
Solution

80. Show that the premises (p ∧ q) ∨ r and r → s imply the conclusion p ∨ s.
We can rewrite the premises (p ∧ q) ∨ r as two clauses using the
Distributive laws: p ∨ r and q ∨ r
Solution

81. Show that the premises (p ∧ q) ∨ r and r → s imply the conclusion p ∨ s.
We can rewrite the premises (p ∧ q) ∨ r as two clauses using the
Distributive laws: p ∨ r and q ∨ r
We can also replace r → s using the implication equivalence
Solution

82. Show that the premises (p ∧ q) ∨ r and r → s imply the conclusion p ∨ s.
We can rewrite the premises (p ∧ q) ∨ r as two clauses using the
Distributive laws: p ∨ r and q ∨ r
We can also replace r → s using the implication equivalence
￢ r ∨ s
Solution

83. Show that the premises (p ∧ q) ∨ r and r → s imply the conclusion p ∨ s.
We can rewrite the premises (p ∧ q) ∨ r as two clauses using the
Distributive laws: p ∨ r and q ∨ r
We can also replace r → s using the implication equivalence
￢ r ∨ s
We can use resolution ((p ∨ q) ∧ (￢p ∨ r)) → (q ∨ r) to conclude p ∨ s.
Solution

84. Rules of Inference
For Quantified Statements

85. Table 2 Rules of Inference for Quantified Statements
Rule of Inference Name
∀x P(x)
∴ P(c)
Universal Instantiation
P(c) for an arbitrary c
∴ ∀x P(x)
Universal Generalization
∃x P(x)
∴ P(c) for some element c
Existential Instantiation
P(c) for some element c
∴ ∃x P(x)
Existential Generalization

86. Show that the premises
“Everyone in this discrete mathematics class has taken a course in
computer science” and
“Marla is a student in this class”
imply the conclusion “Marla has taken a course in computer science.”
Example

87. Let D(x) denote “x is in this discrete mathematics class,”
and let C(x) denote “x has taken a course in computer science.”
Solution

88. Let D(x) denote “x is in this discrete mathematics class,”
and let C(x) denote “x has taken a course in computer science.”
“Everyone in this discrete mathematics class
has taken a course in computer science”
Solution

89. Let D(x) denote “x is in this discrete mathematics class,”
and let C(x) denote “x has taken a course in computer science.”
“Everyone in this discrete mathematics class
has taken a course in computer science”
∀x(D(x) → C(x)) and D(Marla)
Solution

90. Let D(x) denote “x is in this discrete mathematics class,”
and let C(x) denote “x has taken a course in computer science.”
“Marla is a student in this class”
Solution

91. Let D(x) denote “x is in this discrete mathematics class,”
and let C(x) denote “x has taken a course in computer science.”
“Marla is a student in this class”
D(Marla)
Solution

92. Let D(x) denote “x is in this discrete mathematics class,”
and let C(x) denote “x has taken a course in computer science.”
“Marla has taken a course in computer science.”
Solution

93. Let D(x) denote “x is in this discrete mathematics class,”
and let C(x) denote “x has taken a course in computer science.”
“Marla has taken a course in computer science.”
C(Marla)
Solution

94. Premises:
∀x(D(x) → C(x))
D(Marla)
Conclusion: C(Marla)
Solution

95. The following steps can be used to establish the conclusion from the
premises.
Step Reason
1. ∀x(D(x) → C(x)) Premise
Solution

96. The following steps can be used to establish the conclusion from the
premises.
Step Reason
1. ∀x(D(x) → C(x)) Premise
2. D(Marla) → C(Marla) Universal instantiation from (1)
Solution

97. The following steps can be used to establish the conclusion from the
premises.
Step Reason
1. ∀x(D(x) → C(x)) Premise
2. D(Marla) → C(Marla) Universal instantiation from (1)
3. D(Marla) Premise
Solution

98. The following steps can be used to establish the conclusion from the
premises.
Step Reason
1. ∀x(D(x) → C(x)) Premise
2. D(Marla) → C(Marla) Universal instantiation from (1)
3. D(Marla) Premise
You can use other rules of inference!
Solution

99. The following steps can be used to establish the conclusion from the
premises.
Step Reason
1. ∀x(D(x) → C(x)) Premise
2. D(Marla) → C(Marla) Universal instantiation from (1)
3. D(Marla) Premise
4. C(Marla) Modus ponens from (2) and (3)
Solution

100. Show that the premises
“A student in this class has not read the book,” and
“Everyone in this class passed the first exam”
imply the conclusion “Someone who passed the first exam has not read
the book.”
Example

101. Let C(x) be “x is in this class,”
B(x) be “x has read the book,” and
P(x) be “x passed the first exam.”
Solution

102. Let C(x) be “x is in this class,”
B(x) be “x has read the book,” and
P(x) be “x passed the first exam.”
“A student in this class has not read the book.”
Solution

103. Let C(x) be “x is in this class,”
B(x) be “x has read the book,” and
P(x) be “x passed the first exam.”
“A student in this class has not read the book.”
∃x(C(x)∧￢B(x))
Solution

104. Let C(x) be “x is in this class,”
B(x) be “x has read the book,” and
P(x) be “x passed the first exam.”
“Everyone in this class passed the first exam”
Solution

105. Let C(x) be “x is in this class,”
B(x) be “x has read the book,” and
P(x) be “x passed the first exam.”
“Everyone in this class passed the first exam”
∀x(C(x) → P(x))
Solution

106. Let C(x) be “x is in this class,”
B(x) be “x has read the book,” and
P(x) be “x passed the first exam.”
Conclusion: “Someone who passed the first exam
has not read the book.”
Solution

107. Let C(x) be “x is in this class,”
B(x) be “x has read the book,” and
P(x) be “x passed the first exam.”
Conclusion: “Someone who passed the first exam
has not read the book.”
∃x(P(x)∧￢B(x))
Solution

108. Premises:
∃x(C(x)∧￢B(x))
∀x(C(x) → P(x))
Conclusion: ∃x(P(x)∧￢B(x))
Solution

109. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
Solution

110. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
Solution

111. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
3. C(a) Simplification from (2)
Solution

112. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
3. C(a) Simplification from (2)
4. ∀x(C(x) → P(x)) Premise
Solution

113. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
3. C(a) Simplification from (2)
4. ∀x(C(x) → P(x)) Premise
5. C(a) → P(a) Universal instantiation from (4)
Solution

114. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
3. C(a) Simplification from (2)
4. ∀x(C(x) → P(x)) Premise
5. C(a) → P(a) Universal instantiation from (4)
6. P(a) Modus ponens from (3) and (5)
Solution

115. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
3. C(a) Simplification from (2)
4. ∀x(C(x) → P(x)) Premise
5. C(a) → P(a) Universal instantiation from (4)
6. P(a) Modus ponens from (3) and (5)
7. ￢B(a) Simplification from (2)
Solution

116. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
3. C(a) Simplification from (2)
4. ∀x(C(x) → P(x)) Premise
5. C(a) → P(a) Universal instantiation from (4)
6. P(a) Modus ponens from (3) and (5)
7. ￢B(a) Simplification from (2)
8. P(a)∧￢B(a) Conjunction from (6) and (7)
Solution

117. Step Reason
1. ∃x(C(x)∧￢B(x)) Premise
2. C(a)∧￢B(a) Existential instantiation from (1)
3. C(a) Simplification from (2)
4. ∀x(C(x) → P(x)) Premise
5. C(a) → P(a) Universal instantiation from (4)
6. P(a) Modus ponens from (3) and (5)
7. ￢B(a) Simplification from (2)
8. P(a)∧￢B(a) Conjunction from (6) and (7)
9. ∃x(P(x)∧￢B(x)) Existential generalization from (8)
Solution

118. Combining Rules of Inference for
Propositions and Quantified Statements

119. Universal Modus Ponens
∀x(P(x) → Q(x))
P(a), where a is a particular element in the domain
∴ Q(a)
Universal Modus Tollens
∀x(P(x) → Q(x))
¬Q(a), where a is a particular element in the domain
∴ ¬P(a)

120. Any Question?

121. Assignment will be posted later.
Deadline: September 7, 2018 (Friday)
1st Long Exam Schedule
Sept. 18 (Part 1) & Sept. 21 (Part 2),
4PM – 5:30PM @ CL2 and CL4
Announcement

122. A. Which rule of inference is used in each argument below?
1. Alice is a Math major. Therefore, Alice is either a Math major or a CSI major.
2. Jerry is a Math major and a CSI major. Therefore, Jerry is a Math major.
3. If it is rainy, then the pool will be closed. It is rainy. Therefore, the pool is closed.
B. Choose the correct interpretation of each of the following:
E(x) = “x is an earth-like planet.”
L(x) = “x supports life.”
1. ∀x(L(x) → E(x)) 4. ∃x(L(x) → E(x)) 7. ∀x(E(x)) V ∀x(￢E(x))
2. ∀x(E(x)) V ∀x(L(x)) 5. ∃x(E(x)) V ∃x(L(x)) 8. ∃x(E(x)) V ∃x(￢E(x))
3. ￢(∀x(E(x) V L(x))) 6. ￢(∃x(E(x) V L(x))) 9. ∀x(E(x)) V ∃x(￢E(x))
Assignment

123. C. Transform the informal argument below into predicate logic. Then give a formal proof
1. If it does not rain or if is not foggy, then the sailing race will be held and the lifesaving
demonstration will go on. If the sailing race is held, then the trophy will be awarded.
The trophy was not awarded. Therefore, it rained.
2. If I like Discrete Mathematics, then I will study. Either I don’t study or I pass Discrete
Mathematics. If I don’t pass Discrete Mathematics, then I don’t graduate. Therefore, if
I graduate then I like Discrete Mathematics.
3. All Computer Science majors are intelligent. Some Computer Science majors are logical
thinkers. Therefore, some intelligent are logical thinkers.
Assignment