This document discusses tautology, contradiction, and contingency in propositional logic. It defines each concept and provides examples of truth tables to determine if a compound statement is a tautology, contradiction, or contingency. It then gives an enrichment exercise that constructs truth tables for 5 compound statements and identifies which category each one falls into.

1. z
FORMAL LOGIC
Discrete Structures I
FOR-IAN V. SANDOVAL

2. z
Lesson 4
TAUTOLOGY, CONTRADICTION
AND CONTINGENCY
Source: Google Images

3. z
LEARNING OBJECTIVES
❑ Distinguish classes of compound statement

4. z
TAUTOLOGY
❑ a compound statement that is true for all possible
combination of the truth values of the propositional
variables also called logically true.
❑ i.e. (~p ^ q ) → q
p q ~p ~p ^ q (~p ^ q ) → q
T T F F T
T F F F T
F T T T T
F F T F T

5. z
CONTRADICTION
❑ a compound statement that is false for all possible
combination of the truth values of the propositional
variables also called logically false or absurdity.
❑ i.e. (~ p v q ) ⊕ (p → q )
p q ~p ~ p v q p → q (~ p v q ) ⊕ (p → q )
T T F T T F
T F F F F F
F T T T T F
F F T T T F

6. z
CONTINGENCY
❑ a compound statement that can be either true of false,
depending on the truth values of the propositional variables
are neither a tautology nor a contradiction. .
❑ i.e. (p → q ) ^ (p → ~q )
p q p → q ~q p → ~q (p → q ) ^ (p → ~q )
T T T F F F
T F F T T F
F T T F T T
F F T T T T

7. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
❑ Enrichment Exercise
Construct the truth table of the following and
determine whether the compound statement is a tautology,
contradiction and contingency.
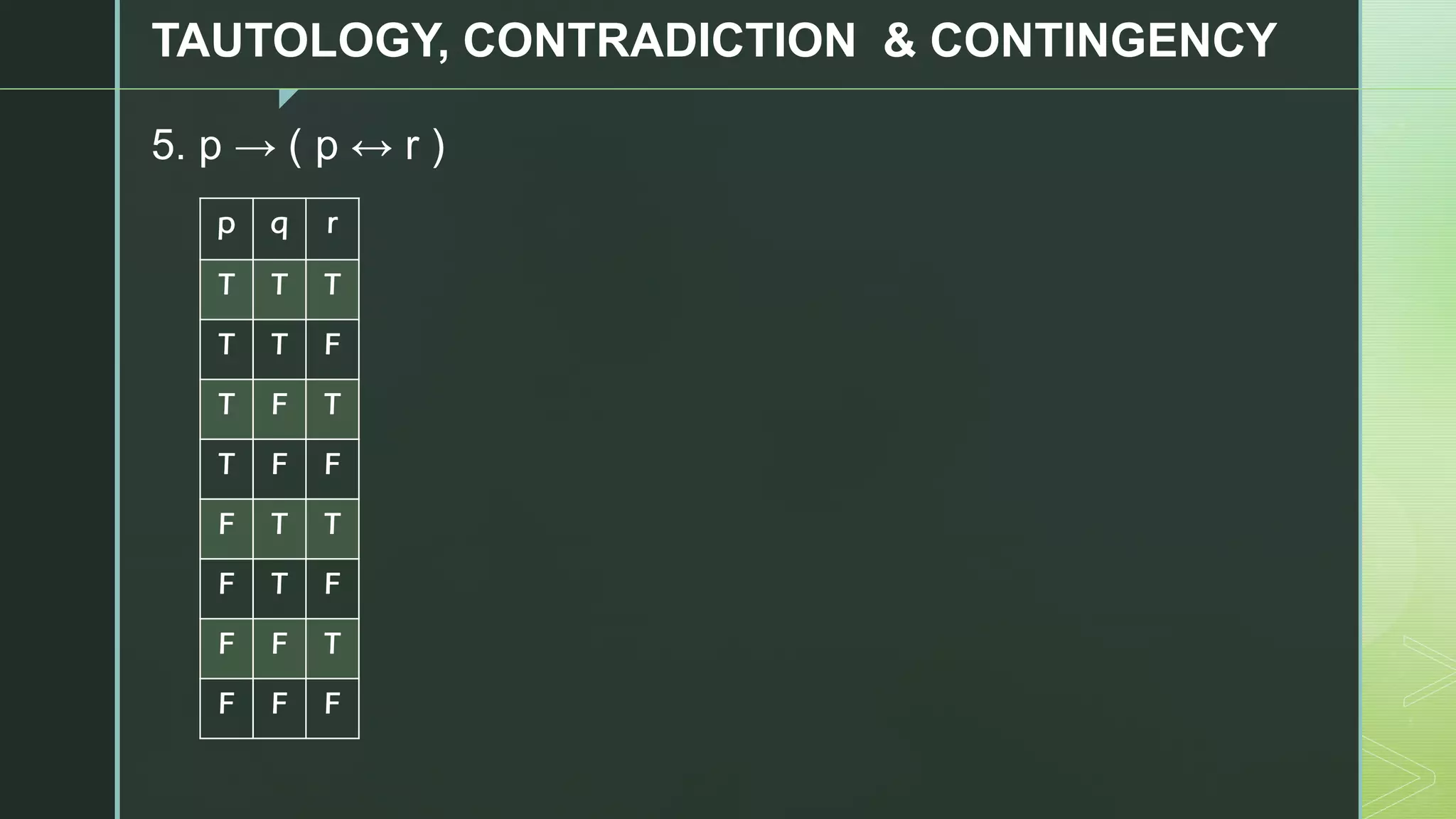
1. p ⊕ (~p ↔ q)
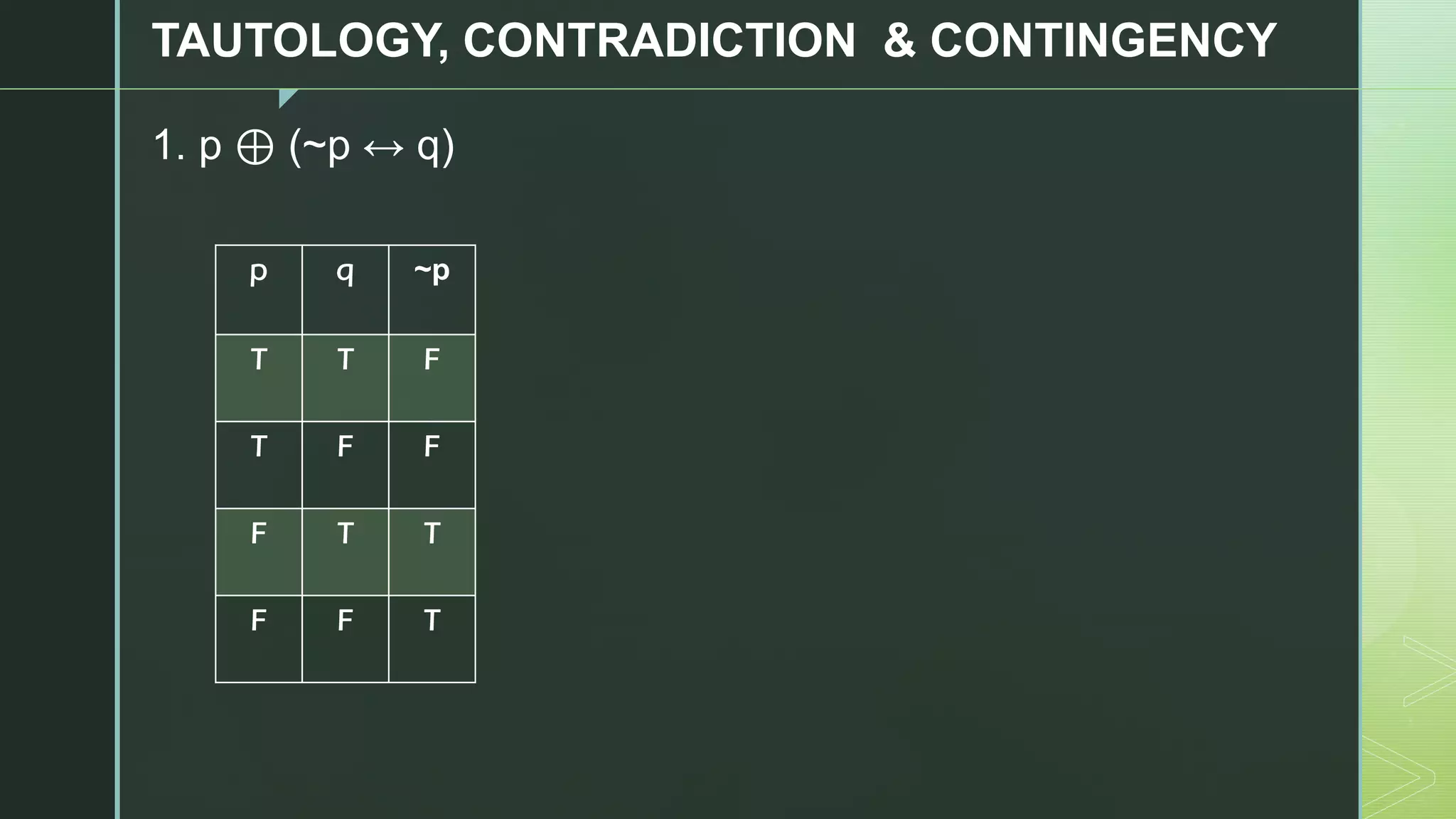
2. [r ^ (p →q)] →q
3. p → (q → r )

8. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
1. p ⊕ (~p ↔ q)
p q
T T
T F
F T
F F

9. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
1. p ⊕ (~p ↔ q)
p q ~p
T T F
T F F
F T T
F F T

10. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
1. p ⊕ (~p ↔ q)
p q ~p (~p ↔ q)
T T F F
T F F T
F T T T
F F T F

11. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
1. p ⊕ (~p ↔ q)
p q ~p (~p ↔ q) p ⊕ (~p ↔ q)
T T F F T
T F F T F
F T T T T
F F T F F
Therefore, p ⊕ (~p ↔ q) is contingency.

12. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
2. [r ^ (p →q)] →q
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F

13. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
2. [r ^ (p →q)] →q
p q r p →q
T T T T
T T F T
T F T F
T F F F
F T T T
F T F T
F F T T
F F F T

14. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
2. [r ^ (p →q)] →q
p q r p →q r ^ (p →q)
T T T T T
T T F T F
T F T F F
T F F F F
F T T T T
F T F T F
F F T T T
F F F T F

15. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
2. [r ^ (p →q)] →q
p q r p →q r ^ (p →q) [r ^ (p →q)] →q
T T T T T T
T T F T F T
T F T F F T
T F F F F T
F T T T T T
F T F T F T
F F T T T F
F F F T F T
Therefore, [r ^ (p →q)] →q is contingency.

16. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
3. p → (q → r )
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F

17. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
3. p → (q → r )
p q r q → r
T T T T
T T F F
T F T T
T F F T
F T T T
F T F F
F F T T
F F F T

18. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
3. p → (q → r )
p q r q → r p → (q → r )
T T T T T
T T F F F
T F T T T
T F F T T
F T T T T
F T F F T
F F T T T
F F F T T
Therefore, [p → (q → r ) is contingency.

19. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
4. [p ^ (p →q)] →q
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F

20. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
4. [p ^ (p →q)] →q
p q r p →q
T T T T
T T F T
T F T F
T F F F
F T T T
F T F T
F F T T
F F F T

21. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
4. [p ^ (p →q)] →q
p q r p →q p ^ (p →q)
T T T T T
T T F T T
T F T F F
T F F F F
F T T T F
F T F T F
F F T T F
F F F T f

22. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
4. [p ^ (p →q)] →q
p q r p →q p ^ (p →q) [p^ (p →q)] →q
T T T T T T
T T F T T T
T F T F F T
T F F F F T
F T T T F T
F T F T F T
F F T T F T
F F F T f T
Therefore, [p ^ (p →q)] →q is tautology.

23. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
5. p → ( p ↔ r )
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F

24. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
5. p → ( p ↔ r )
p q r p ↔ r
T T T T
T T F F
T F T T
T F F F
F T T F
F T F T
F F T F
F F F T

25. z
TAUTOLOGY, CONTRADICTION & CONTINGENCY
5. p → ( p ↔ r )
p q r p ↔ r p → (p ↔ r )
T T T T T
T T F F F
T F T T T
T F F F F
F T T F T
F T F T T
F F T F T
F F F T T
Therefore, p → ( p ↔ r ) is contingency.

26. z
• Levin, O. (2019). Discrete Mathematics: An Open Introduction 3rd Edition. Colorado: School of Mathematics Science
University of Colorado.
• Aslam, A. (2016). Proposition in Discrete Mathematics retrieved from https://www.slideshare.net/AdilAslam4/chapter-1-
propositions-in-discrete-mathematics
• Operator Precedence retrieved from http://intrologic.stanford.edu/glossary/operator_precedence.html
REFERENCES