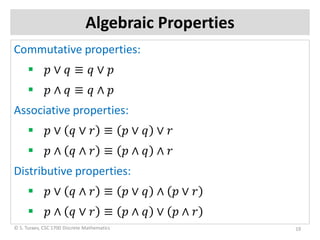
This document defines logical propositions, statements, and logical operations such as negation, conjunction, disjunction, implication, equivalence, and quantification. Propositions can be combined using logical operations to form compound statements. Truth tables are used to evaluate compound statements based on the truth values of the component propositions. Logical properties such as commutativity, associativity, distributivity, idempotence and negation are also discussed.

1. Logic

2. Propositions and Logical Operations
Definition: A statement or proposition is a declarative
sentence that is either true (T) or false (F), but not both.
Example: Which of the following are statements?
a. It is raining.
b. 2 + 3 = 5
c. Do you speak English?
d. 3 − 𝑥𝑥 = 5
e. Take two aspirins.
© S. Turaev, CSC 1700 Discrete Mathematics 2

3. Propositions and Logical Operations
 The letters 𝑝𝑝, 𝑞𝑞, 𝑟𝑟 are denote propositional variables
• 𝑝𝑝: I am teaching.
• 𝑞𝑞: 3 × 23 = 70
 Compound statements: propositional variables
combined by logical connectives (and, or, if … then, …):
• 𝑝𝑝 and 𝑞𝑞.
• 𝑝𝑝 or 𝑞𝑞.
• If 𝑝𝑝 then 𝑞𝑞.
3© S. Turaev, CSC 1700 Discrete Mathematics

4. Propositions and Logical Operations
Definition: If 𝑝𝑝 is a statement, the negation of 𝑝𝑝 is the
statement not 𝑝𝑝, denoted by ~𝑝𝑝 (sometimes, ¬𝑝𝑝, ̅𝑝𝑝).
~𝑝𝑝: “It is not the case that 𝑝𝑝”.
Example:
 𝑝𝑝: 2 + 3 > 1 ~𝑝𝑝:
 𝑞𝑞: It is cold. ~𝑝𝑝:
4© S. Turaev, CSC 1700 Discrete Mathematics
𝑝𝑝 ~𝑝𝑝
T F
F T

5. Propositions and Logical Operations
Definition: If 𝑝𝑝 and 𝑞𝑞 are statements, the conjunction of 𝑝𝑝
and 𝑞𝑞 is the compound statement 𝑝𝑝 and 𝑞𝑞, denoted by
𝑝𝑝 ∧ 𝑞𝑞.
Example:
 𝑝𝑝: It is raining. 𝑞𝑞: It is cold.
 𝑝𝑝: 2 < 3. 𝑞𝑞: −3 < −2.
 𝑝𝑝 ∧ 𝑞𝑞:
5© S. Turaev, CSC 1700 Discrete Mathematics
𝑝𝑝 𝑞𝑞 𝑝𝑝 ∧ 𝑞𝑞
T T T
T F F
F T F
F F F

6. Propositions and Logical Operations
Definition: If 𝑝𝑝 and 𝑞𝑞 are statements, the disjunction of 𝑝𝑝
and 𝑞𝑞 is the compound statement 𝑝𝑝 or 𝑞𝑞, denoted by 𝑝𝑝 ∨
𝑞𝑞.
Example:
 𝑝𝑝: It is raining. 𝑞𝑞: It is cold.
 𝑝𝑝: 2 < 3. 𝑞𝑞: −3 < −2.
 𝑝𝑝 ∨ 𝑞𝑞:
6© S. Turaev, CSC 1700 Discrete Mathematics
𝑝𝑝 𝑞𝑞 𝑝𝑝 ∧ 𝑞𝑞
T T T
T F T
F T T
F F F

7. Propositions and Logical Operations
A compound statement may have many components:
𝑝𝑝 ∨ (𝑞𝑞 ∧ (~ 𝑝𝑝 ∧ 𝑟𝑟 ))
Example: Make a truth table for 𝑝𝑝 ∧ 𝑞𝑞 ∨ ~𝑝𝑝.
7© S. Turaev, CSC 1700 Discrete Mathematics
𝑝𝑝 𝑞𝑞 𝑝𝑝 ∧ 𝑞𝑞 ~𝑝𝑝 ∨
T T
T F
F T
F F

8. Propositions and Logical Operations
Definition: If 𝑝𝑝 and 𝑞𝑞 are statements, the compound
statement “if 𝑝𝑝 then 𝑞𝑞”, denoted 𝑝𝑝 ⇒ 𝑞𝑞, is called a
conditional statement or implication.
The statement 𝑝𝑝 is called antecedent or hypothesis and 𝑞𝑞
is called the consequent or conclusion.
Example:
 𝑝𝑝: I am hungry. 𝑞𝑞: I will eat.
 𝑝𝑝: It is snowing. 𝑞𝑞: 3 + 2 = 5.
 𝑝𝑝 ⇒ 𝑞𝑞:
8© S. Turaev, CSC 1700 Discrete Mathematics
𝑝𝑝 𝑞𝑞 𝑝𝑝 ⇒ 𝑞𝑞
T T T
T F F
F T T
F F T

9. Propositions and Logical Operations
Definition: If 𝑝𝑝 ⇒ 𝑞𝑞 is an implication, then
 the converse of 𝑝𝑝 ⇒ 𝑞𝑞 is the implication 𝑞𝑞 ⇒ 𝑝𝑝
 the inverse of 𝑝𝑝 ⇒ 𝑞𝑞 is the implication ~𝑝𝑝 ⇒ ~𝑞𝑞
 the contrapositive of 𝑝𝑝 ⇒ 𝑞𝑞 is the implication ~𝑞𝑞 ⇒
~𝑝𝑝
Example: 𝑝𝑝 ⇒ 𝑞𝑞: “If it is raining then I get wet” then
𝑞𝑞 ⇒ 𝑝𝑝, ~𝑝𝑝 ⇒ ~𝑞𝑞, ~𝑞𝑞 ⇒ ~𝑝𝑝?
9© S. Turaev, CSC 1700 Discrete Mathematics

10. Propositions and Logical Operations
Definition: If 𝑝𝑝 and 𝑞𝑞 are statements, the compound
statement “𝑝𝑝 if and only if 𝑞𝑞”, denoted 𝑝𝑝 ⇔ 𝑞𝑞, is called
an equivalence or biconditional.
Example:
 𝑝𝑝: 3 > 2. 𝑞𝑞: 0 < 3 − 2.
 𝑝𝑝: It is snowing. 𝑞𝑞: 3 + 2 = 5.
 𝑝𝑝 ⇔ 𝑞𝑞:
10© S. Turaev, CSC 1700 Discrete Mathematics
𝑝𝑝 𝑞𝑞 𝑝𝑝 ⇒ 𝑞𝑞
T T T
T F F
F T F
F F T

11. Propositions and Logical Operations
Example: Compute the truth table of the statement
𝑝𝑝 ⇒ 𝑞𝑞 ⇔ (~𝑞𝑞 ⇒ ~𝑝𝑝)
11© S. Turaev, CSC 1700 Discrete Mathematics
𝑝𝑝 𝑞𝑞 𝑝𝑝 ⇒ 𝑞𝑞 ~𝑞𝑞 ~𝑝𝑝 ~𝑞𝑞 ⇒ ~𝑝𝑝 ⇔
T T
T F
F T
F F

12. Propositions and Logical Operations
Definition: A statement that is true for all possible values
of its propositional variables is called a tautology.
Definition: A statement that is false for all possible values
of its propositional variables is called a contradiction or
an absurdity.
Definition: A statement that can be either true or false
for all possible values of its propositional variables is
called contingency.
12© S. Turaev, CSC 1700 Discrete Mathematics

13. Propositions and Logical Operations
Example:
 The statement 𝑝𝑝 ∨ ~𝑝𝑝:
 The statement 𝑝𝑝 ∧ ~𝑝𝑝:
 The statement 𝑝𝑝 ⇒ 𝑞𝑞 ∧ (𝑝𝑝 ∨ 𝑞𝑞):
13© S. Turaev, CSC 1700 Discrete Mathematics

14. Propositions and Logical Operations
Definition: We say that the statements 𝑝𝑝 and 𝑞𝑞 are
logically equivalent (or simply equivalent), denoted by
𝑝𝑝 ≡ 𝑞𝑞, if 𝑝𝑝 ⇔ 𝑞𝑞 is tautology.
Example: Show that
 𝑝𝑝 ∨ 𝑞𝑞 ≡ 𝑞𝑞 ∨ 𝑝𝑝
 𝑝𝑝 ⇒ 𝑞𝑞 ≡ ~𝑝𝑝 ∨ 𝑞𝑞
14© S. Turaev, CSC 1700 Discrete Mathematics

15. Propositions and Logical Operations
Definition: A predicate or a propositional function is a
noun/verb phrase template that describes a property of
objects, or a relationship among objects represented by
the variables:
Example: 𝑃𝑃 𝑥𝑥 : “𝑥𝑥 is integer less than 8.”
 𝑃𝑃 1 =
 𝑃𝑃 10 =
 𝑃𝑃 −11 =
15© S. Turaev, CSC 1700 Discrete Mathematics

16. Propositions and Logical Operations
Definition: The universal quantification of a predicate
𝑃𝑃 𝑥𝑥 is the statement “For all values of 𝑥𝑥 (for every 𝑥𝑥, for
each 𝑥𝑥, for any 𝑥𝑥), 𝑃𝑃 𝑥𝑥 is true” and is denoted by
∀𝑥𝑥𝑥𝑥 𝑥𝑥 .
Example: 𝑃𝑃 𝑥𝑥 : “− −𝑥𝑥 = 𝑥𝑥” is a predicate that is true
for all real numbers.
∀𝑥𝑥𝑥𝑥 𝑥𝑥 =
Example: 𝑄𝑄 𝑥𝑥 : “𝑥𝑥 + 1 < 4”.
∀𝑥𝑥𝑥𝑥 𝑥𝑥 =
16© S. Turaev, CSC 1700 Discrete Mathematics

17. Propositions and Logical Operations
A predicate may contain several variables.
Example: 𝑄𝑄 𝑥𝑥, 𝑦𝑦 : 𝑥𝑥 + 𝑦𝑦 = 𝑦𝑦 + 𝑥𝑥
∀𝑥𝑥∀𝑦𝑦𝑦𝑦 𝑥𝑥, 𝑦𝑦 =
Example: Write the following statement in the form of a
predicate and quantifier:
“The sum of any two integers is even number.”
17© S. Turaev, CSC 1700 Discrete Mathematics

18. Propositions and Logical Operations
Definition: The existential quantification of a predicate
𝑃𝑃 𝑥𝑥 is the statement “There exists a value of 𝑥𝑥, for
which 𝑃𝑃 𝑥𝑥 is true” and is denoted by ∃𝑥𝑥𝑥𝑥 𝑥𝑥 .
Example: 𝑃𝑃 𝑥𝑥 : “−𝑥𝑥 = 𝑥𝑥”.
∃𝑥𝑥𝑥𝑥 𝑥𝑥 =
Example: 𝑄𝑄 𝑥𝑥 : “𝑥𝑥 + 1 < 4”.
∃𝑥𝑥𝑥𝑥 𝑥𝑥 =
18© S. Turaev, CSC 1700 Discrete Mathematics

19. Algebraic Properties
Commutative properties:
 𝑝𝑝 ∨ 𝑞𝑞 ≡ 𝑞𝑞 ∨ 𝑝𝑝
 𝑝𝑝 ∧ 𝑞𝑞 ≡ 𝑞𝑞 ∧ 𝑝𝑝
Associative properties:
 𝑝𝑝 ∨ 𝑞𝑞 ∨ 𝑟𝑟 ≡ 𝑝𝑝 ∨ 𝑞𝑞 ∨ 𝑟𝑟
 𝑝𝑝 ∧ 𝑞𝑞 ∧ 𝑟𝑟 ≡ 𝑝𝑝 ∧ 𝑞𝑞 ∧ 𝑟𝑟
Distributive properties:
 𝑝𝑝 ∨ 𝑞𝑞 ∧ 𝑟𝑟 ≡ 𝑝𝑝 ∨ 𝑞𝑞 ∧ 𝑝𝑝 ∨ 𝑟𝑟
 𝑝𝑝 ∧ 𝑞𝑞 ∨ 𝑟𝑟 ≡ 𝑝𝑝 ∧ 𝑞𝑞 ∨ 𝑝𝑝 ∧ 𝑟𝑟
19© S. Turaev, CSC 1700 Discrete Mathematics

20. Algebraic Properties
Idempotent properties:
 𝑝𝑝 ∨ 𝑝𝑝 ≡ 𝑝𝑝
 𝑝𝑝 ∧ 𝑝𝑝 ≡ 𝑝𝑝
Properties of negation:
 ~(~𝑝𝑝) ≡ 𝑝𝑝
 ~ 𝑝𝑝 ∨ 𝑞𝑞 ≡ ~𝑝𝑝 ∧ ~𝑞𝑞
 ~ 𝑝𝑝 ∧ 𝑞𝑞 ≡ ~𝑝𝑝 ∨ ~𝑞𝑞
20© S. Turaev, CSC 1700 Discrete Mathematics

21. Algebraic Properties
Properties of implication:
 𝑝𝑝 ⇒ 𝑞𝑞 ≡ ~𝑝𝑝 ∨ 𝑞𝑞
 𝑝𝑝 ⇒ 𝑞𝑞 ≡ ~𝑞𝑞 ⇒ ~𝑝𝑝
 𝑝𝑝 ⇔ 𝑞𝑞 ≡ 𝑝𝑝 ⇒ 𝑞𝑞 ∧ 𝑞𝑞 ⇒ 𝑝𝑝
 ~ 𝑝𝑝 ⇒ 𝑞𝑞 ≡ 𝑝𝑝 ⇒ ~𝑞𝑞
 ~ 𝑝𝑝 ⇔ 𝑞𝑞 ≡ 𝑝𝑝 ∧ ~𝑞𝑞 ∨ 𝑞𝑞 ∧ ~𝑝𝑝
21© S. Turaev, CSC 1700 Discrete Mathematics

22. Algebraic Properties
Properties of quantifiers:
 ~ ∀𝑥𝑥𝑥𝑥 𝑥𝑥 ≡ ∃𝑥𝑥~𝑃𝑃 𝑥𝑥
 ~ ∃𝑥𝑥𝑥𝑥 𝑥𝑥 ≡ ∀𝑥𝑥~𝑃𝑃 𝑥𝑥
 ∃𝑥𝑥 𝑃𝑃 𝑥𝑥 ⇒ 𝑄𝑄 𝑥𝑥 ≡ ∀𝑥𝑥𝑥𝑥 𝑥𝑥 ⇒ ∃𝑥𝑥𝑥𝑥 𝑥𝑥
 ∃𝑥𝑥 𝑃𝑃 𝑥𝑥 ∨ 𝑄𝑄 𝑥𝑥 ≡ ∃𝑥𝑥𝑥𝑥 𝑥𝑥 ∨ ∃𝑥𝑥𝑥𝑥 𝑥𝑥
 ∀𝑥𝑥 𝑃𝑃 𝑥𝑥 ∧ 𝑄𝑄 𝑥𝑥 ≡ ∀𝑥𝑥𝑥𝑥 𝑥𝑥 ∧ ∀𝑥𝑥𝑥𝑥 𝑥𝑥
 ∀𝑥𝑥𝑥𝑥 𝑥𝑥 ∨ ∀𝑥𝑥𝑥𝑥 𝑥𝑥 ⇒ ∀𝑥𝑥 𝑃𝑃 𝑥𝑥 ∨ 𝑄𝑄 𝑥𝑥
 ∃𝑥𝑥 𝑃𝑃 𝑥𝑥 ∧ 𝑄𝑄 𝑥𝑥 ⇒ ∃𝑥𝑥𝑥𝑥 𝑥𝑥 ∨ ∃𝑥𝑥𝑥𝑥 𝑥𝑥
22© S. Turaev, CSC 1700 Discrete Mathematics

23. Algebraic Properties
Tautologies:
 𝑝𝑝 ⇒ 𝑞𝑞 ∧ 𝑞𝑞 ⇒ 𝑟𝑟 ⇒ (𝑝𝑝 ⇒ 𝑟𝑟)
23© S. Turaev, CSC 1700 Discrete Mathematics
 𝑝𝑝 ∧ 𝑞𝑞 ⇒ 𝑝𝑝
 𝑝𝑝 ⇒ 𝑝𝑝 ∨ 𝑞𝑞
 ~𝑝𝑝 ⇒ 𝑝𝑝 ⇒ 𝑞𝑞
 𝑝𝑝 ∧ 𝑝𝑝 ⇒ 𝑞𝑞 ⇒ 𝑞𝑞
 ~𝑞𝑞 ∧ 𝑝𝑝 ⇒ 𝑞𝑞 ⇒ ~𝑝𝑝
 𝑝𝑝 ∧ 𝑞𝑞 ⇒ 𝑞𝑞
 𝑞𝑞 ⇒ 𝑝𝑝 ∧ 𝑞𝑞
 ~ 𝑝𝑝 ⇒ 𝑞𝑞 ⇒ 𝑝𝑝
 ~𝑝𝑝 ∧ 𝑝𝑝 ∨ 𝑞𝑞 ⇒ 𝑞𝑞