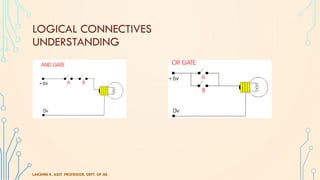
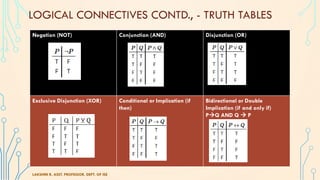
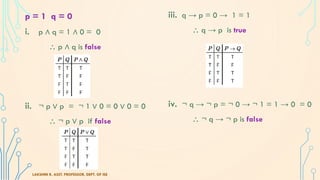
The document discusses fundamentals of logic including propositions, truth values, logical connectives, and examples. It defines a proposition as a statement that can be either true or false, but not both. Truth values are defined as the truth or falsity of a proposition. Logical connectives like negation, conjunction, disjunction are introduced to form compound propositions from simple propositions. Several examples are given to illustrate logical connectives and truth tables are used to determine truth values of compound propositions. Problems involving determining truth values and identifying tautologies, contradictions and contingencies are also presented.

1. FUNDAMENTALS OF LOGIC
BY
LAKSHMI R
ASST. PROFESSOR
DEPARTMENT OF ISE

2. PROPOSITION
• Statement or declaration which in a given context, can be either true or false,
but not both.
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
Propositions:
i. France borders Belgium
ii. 8 is an even number
(May not be true always!!)
i. Barcelona is in Italy
ii. 2 is rational
Not Propositions:
i. Can you pass the sheet?
ii. Listen to me.
iii. What a lovely dress!
iv. Give me a cup of tea.

3. TRUTH VALUE
• The truth or falsity of a proposition is called its truth value
Propositions:
i. France borders Belgium – with truth value TRUE (1)
ii. 8 is an even number – with truth value TRUE (1)
iii. Barcelona is in Italy - with truth value FALSE (0)
iv. 2 is rational - with truth value FALSE (0)
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE

4. LOGICAL CONNECTIVES
• New phrases are obtained – not, or, and, if then, if and only if etc.,
• Compound propositions - The new proposition obtained by the use of logical
connectives eg: France borders Belgium and Norway borders Sweden
• Components or primitives – original propositions from which a compound
proposition is obtained.
• Simple propositions – Proposition that do not contain any logical connectives
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE

5. LOGICAL CONNECTIVES
UNDERSTANDING
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE

6. LOGICAL CONNECTIVES CONTD., - TRUTH TABLES
Negation (NOT) Conjunction (AND) Disjunction (OR)
Exclusive Disjunction (XOR) Conditional or Implication (if
then)
Bidirectional or Double
Implication (if and only if)
PQ AND Q  P
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE

7. LOGICAL CONNECTIVES CONTD., EXAMPLES
Negation:
p: Madrid is a capital city
¬p : Madrid is not a capital city
Conjunction:
P: 2 is an irrational number
Q: 2 + 5 = 7
P ∧ Q : 2 is an irrational number and
2 + 5 = 7
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
Disjunction:
p: Triangles have three sides
q : Bangalore is in Karnataka
p ∨ q : Triangles have three sides or
Bangalore is in Karnataka
Exclusive Disjunction:
p: Alex eats an apple
q: Alex eats an orange
p ⊻ q : Alex eats an apple or Alex
eats an orange, but not both

8. LOGICAL CONNECTIVES CONTD., EXAMPLES
Conditional
p: I weigh more than 120 pounds
q : I shall enrol in an exercise class
p → q : if I weigh more than 120 pounds, then I shall enrol in an
exercise class
Bidirectional: (p → q) ∧ (q → p)
p: I shall enrol in an exercise class
q : I weigh more than 120 pounds
p ↔ q : I shall enrol in an exercise class if and only if I weigh more
than 120 pounds
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE

9. PROBLEM 1:
Let s, t, and u denote the following primitive statements.
s: Zac goes out for a walk
t: The moon is out
u: It is snowing
Express the following compound propositions in words
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
(t ∧ ¬u) → s
¬ ∧ ∨ ⊻ → ↔
If the moon is out and it is not snowing, then Zac goes out for a walk
t → (¬u → s) If the moon is out then it is not snowing then Zac goes out for a walk
¬(s ↔ (u ∨ t))
It is not the case that Zac goes out for a walk if and only if it is snowing or
the moon is out
u ∧ s It is snowing and Zac goes out for a walk
(u ∧ ¬t) → ¬s If it is snowing and the moo is not out, then Zac does not go out for a walk
s ↔ t Zac goes out for a walk if and only the moon is out
p → q ---- if p, then q
p ↔ q ---- p if and only if q

10. PROBLEM 2:
Construct truth table for the following compound propositions
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
¬ ∧ ∨ ⊻ → ↔
p ∧ ¬q
p → ¬q
p q ¬q p → ¬q
0 0 1 1
0 1 0 1
1 0 1 1
1 1 0 0
p q ¬q p ∧ ¬q
0 0 1 0
0 1 0 0
1 0 1 1
1 1 0 0
q ∧ (¬r → p)
p q r ¬r ¬r → p q ∧ (¬r → p)
0 0 0 1 0 0
0 0 1 0 1 0
0 1 0 1 0 0
0 1 1 0 1 1
1 0 0 1 1 0
1 0 1 0 1 0
1 1 0 1 1 1
1 1 1 0 1 1
(p ∨ q) ∧ r
p ∨ (q ∨ r)
(p ∧ q) → ¬r
Try this!

11. Let p and q be primitive statements for which the implication p → q is false.
Determine the truth values of the following
i. p ∧ q
ii. ¬ p ∨ q
iii.q → p
iv.¬ q → ¬ p
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
PROBLEM 3: ¬ ∧ ∨ ⊻ → ↔
Given: p → q is false
p → q is false only when p is true and
q is false
 Truth value of p is 1 (or true)
Truth value of q is 0 (or false)
Solution:

12. p = 1 q = 0
i. p ∧ q = 1 ∧ 0 = 0
 p ∧ q is false
ii. ¬ p ∨ p = ¬ 1 ∨ 0 = 0 ∨ 0 = 0
 ¬ p ∨ p if false
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
iii. q → p = 0 → 1 = 1
 q → p is true
iv. ¬ q → ¬ p = ¬ 0 → ¬ 1 = 1 → 0 = 0
 ¬ q → ¬ p is false

13. Let p, q, and r be propositions having truth values 0, 0, and 1 respectively. Find
the truth values of the following
i. (p ∨ q) ∨ r
ii. (p ∧ q) ∧ r
iii. (p ∧ q) → r
iv. p → (q ∧ r)
v. p ∧ (r → q)
vi. p → (q → ¬ r)
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
¬ ∧ ∨ ⊻ → ↔PROBLEM 4:
Answers:
i. True
ii. False
iii. True
iv. True
v. False
vi. True

14. • Find the possible truth values of p, q, and r in the following cases.
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
PROBLEM 5:
p → (q ∨ r) is false
¬ ∧ ∨ ⊻ → ↔
Solution
⁃ p → (q ∨ r) = 0
⁃ Only if p =1 and (q ∨ r) = 0
⁃ (q ∨ r) is false only if q = 0, r = 0
p ∧ (q → r) is true
Solution
⁃ This is possible only when
⁃ p = 1 and (q → r) = 1
⁃ (q → r) = 1 in 3 cases (recall the truth table
of implication)
p q r
1 0 0
p q r
1 0 0
1 0 1
1 1 1

15. • If a proposition q has truth value 1, determine all truth value assignments for the
primitive propositions p, q, r, and s for which the truth value of the following
proposition is 1
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
PROBLEM 6: ¬ ∧ ∨ ⊻ → ↔
[ q → { (¬p ∨ r ) ∧ ¬s } ] ∧ {¬s → (¬r ∧ q ) }
[ q → { (¬p ∨ r ) ∧ ¬s } ] ∧ {¬s → (¬r ∧ q ) }
1 1
q → { (¬p ∨ r ) ∧ ¬s } = 1
---- eq(1)
¬s → (¬r ∧ q ) = 1 ---- eq(2)
Given, q = 1. Substitute this.

16. q → { (¬p ∨ r ) ∧ ¬s } = 1
Substituting q = 1 in eq(1)
⇒ 1 → { (¬p ∨ r ) ∧ ¬s } = 1
This is possible only if
{ (¬p ∨ r ) ∧ ¬s } = 1
⇒ ¬s = 1 and
(¬p ∨ r ) = 1 --- eq (3)
If ¬s = 1, s = 0
¬s → (¬r ∧ q ) = 1
We got, ¬s = 1
Substituting ¬s = 1 and
q = 1 in eq(2)
1 → (¬r ∧ 1 ) = 1
This is possible only if
(¬r ∧ 1 ) = 1
⇒ ¬r = 1
If ¬r = 1 , r = 0
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
Substituting r in eq (3),
(¬p ∨ 0 ) = 1
¬p has to be 1 to get
the above equation
right.
Therefore, p = 0
Truth values
p q r s
0 1 0 0
1 2 3

17. Give the conjunction and disjunction of p and q, also indicate the truth value.
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
PROBLEM 7: ¬ ∧ ∨ ⊻ → ↔
i)
p: 4 is a perfect square
q: 27 is a prime number
ii)
p: 5 is divisible by 2
q: 7 is a multiple of 5
Conjunction: p ∧ q ⇒ 4 is a perfect
square and 27 is a prime number
p = 1, q = 0
 p ∧ q is False
Disjunction: p ∨ q ⇒ 4 is a perfect
square or 27 is a prime number
p = 1, q = 0
 p ∨ q is true
Conjunction: p ∧ q ⇒ 5 is divisible by 2
and 7 is a multiple of 5
p = 0, q = 0
 p ∧ q is False
Disjunction: p ∨ q ⇒ 5 is divisible by 2
and 7 is a multiple of 5
p = 0, q = 0
 p ∨ q is False

18. From the information given in each of the following
determine the truth value required.
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
Solve it!!!
a. p ∧ q is false and p is true. Find the truth value of q
b. p → q is true, q is false. Find the truth value of p
c. P ↔ q is true, p is false. Find the truth value of q.
¬ ∧ ∨ ⊻ → ↔PROBLEM 8:

19. TAUTOLOGY, CONTRADICTION AND
CONTINGENCY
• Tautology – Always true regardless of the truth values of its components
Eg: p ∨ ¬ p
• Contradiction – Always false
Eg: p ∧ ¬ p
• Contingency – Neither tautology not contingency
Eg: ¬ p ∧ q
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
p ¬ p p ∨ ¬ p
0 1 1
1 0 1
p ¬ p p ∧ ¬ p
0 1 0
1 0 0
p q ¬ p ¬ p ∧ q
0 0 1 0
0 1 1 1
1 0 0 0
1 1 0 0

20. i. (p ⊻ q) ∨ (p ↔ q) is a tautology
ii. (p ⊻ q) ∧ (p ↔ q) is a contradiction
iii. (p ⊻ q) ∧ (p → q) is a contingency
iv. P → (p ∨ q) is a tautology
LAKSHMI R, ASST. PROFESSOR, DEPT. OF ISE
PROBLEM 9: SHOW THAT
Another way of asking the same question
Show that the truth values of the following
compound propositions are independent of the
truth values of their components.