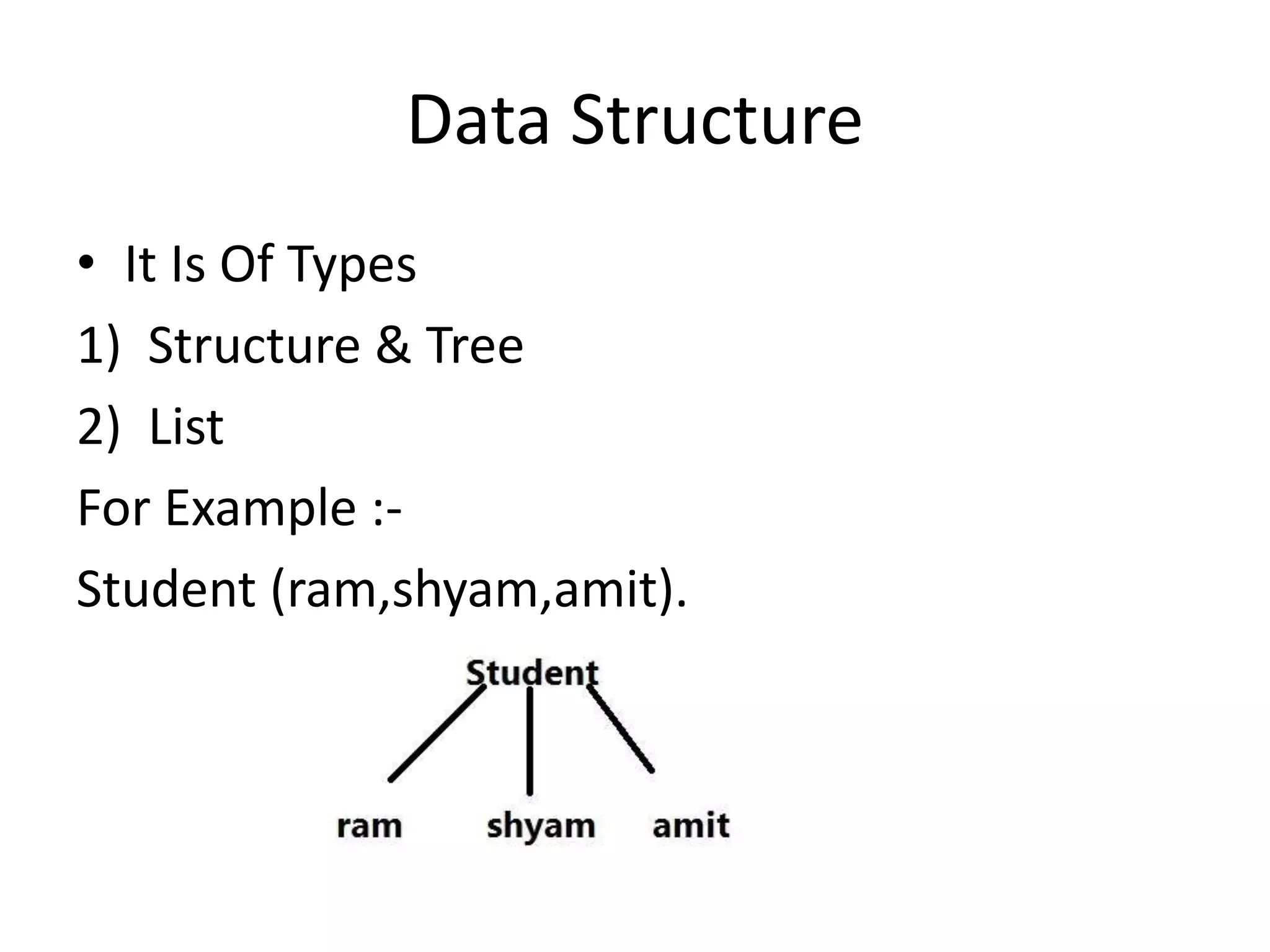
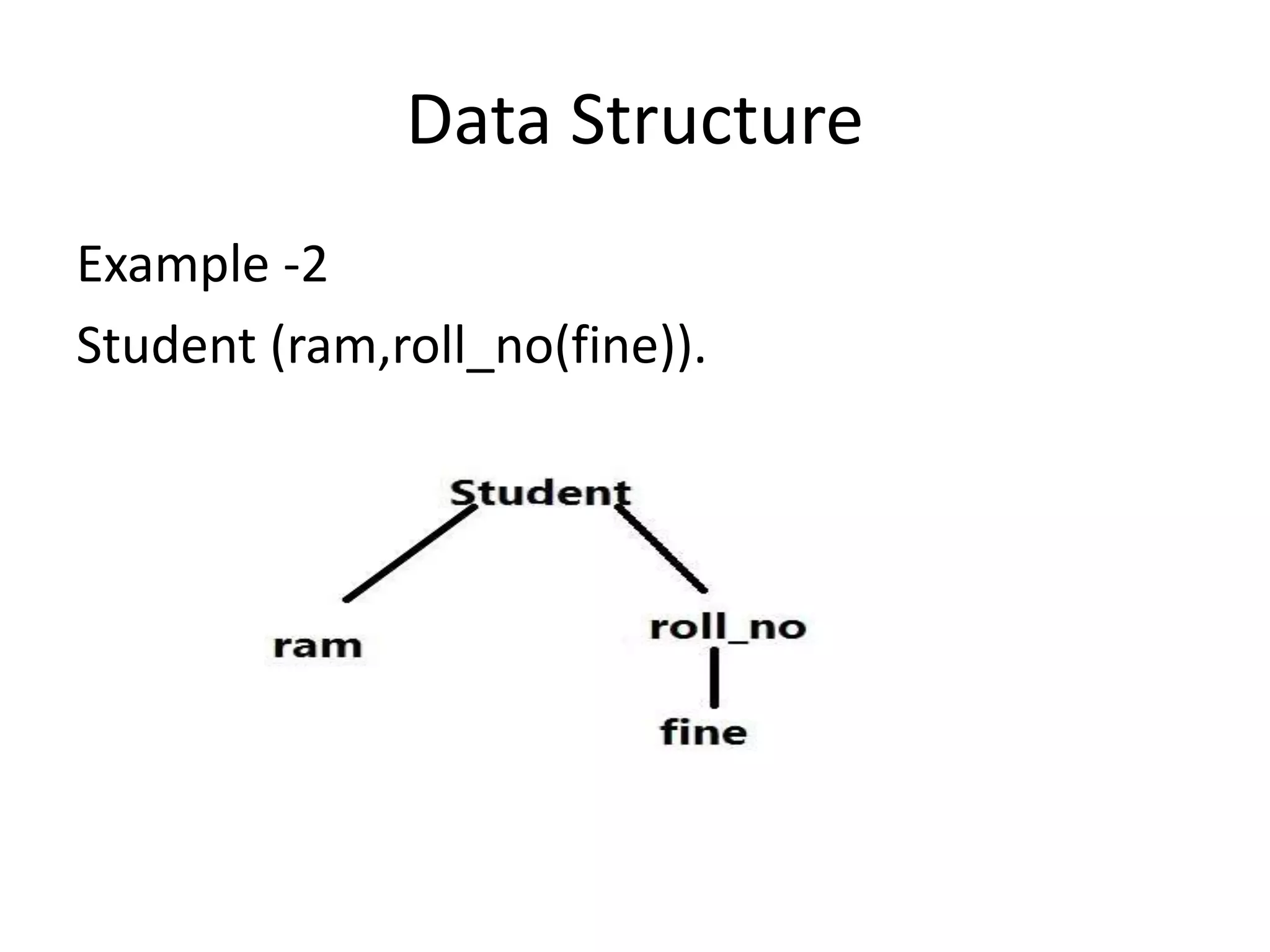
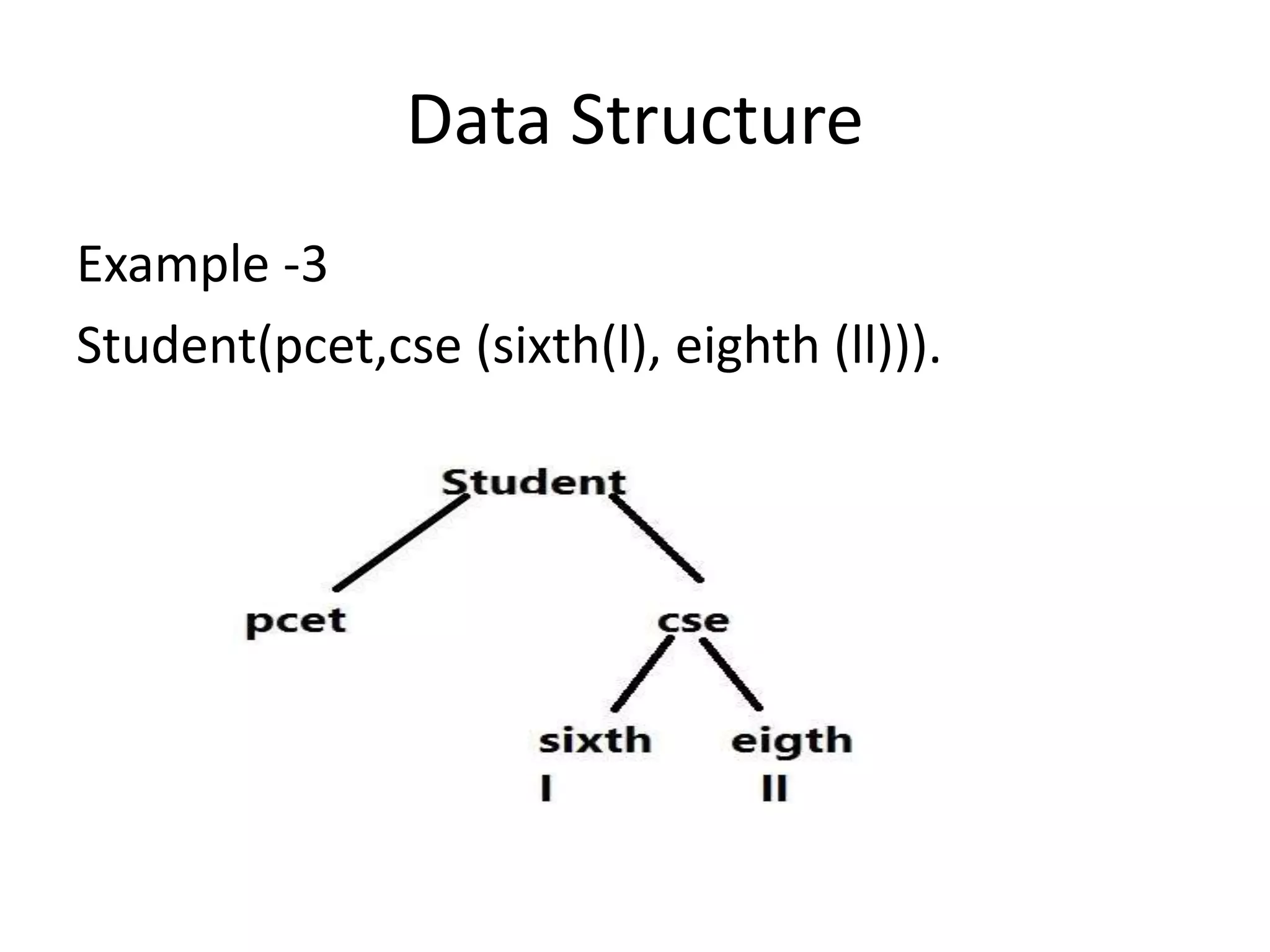
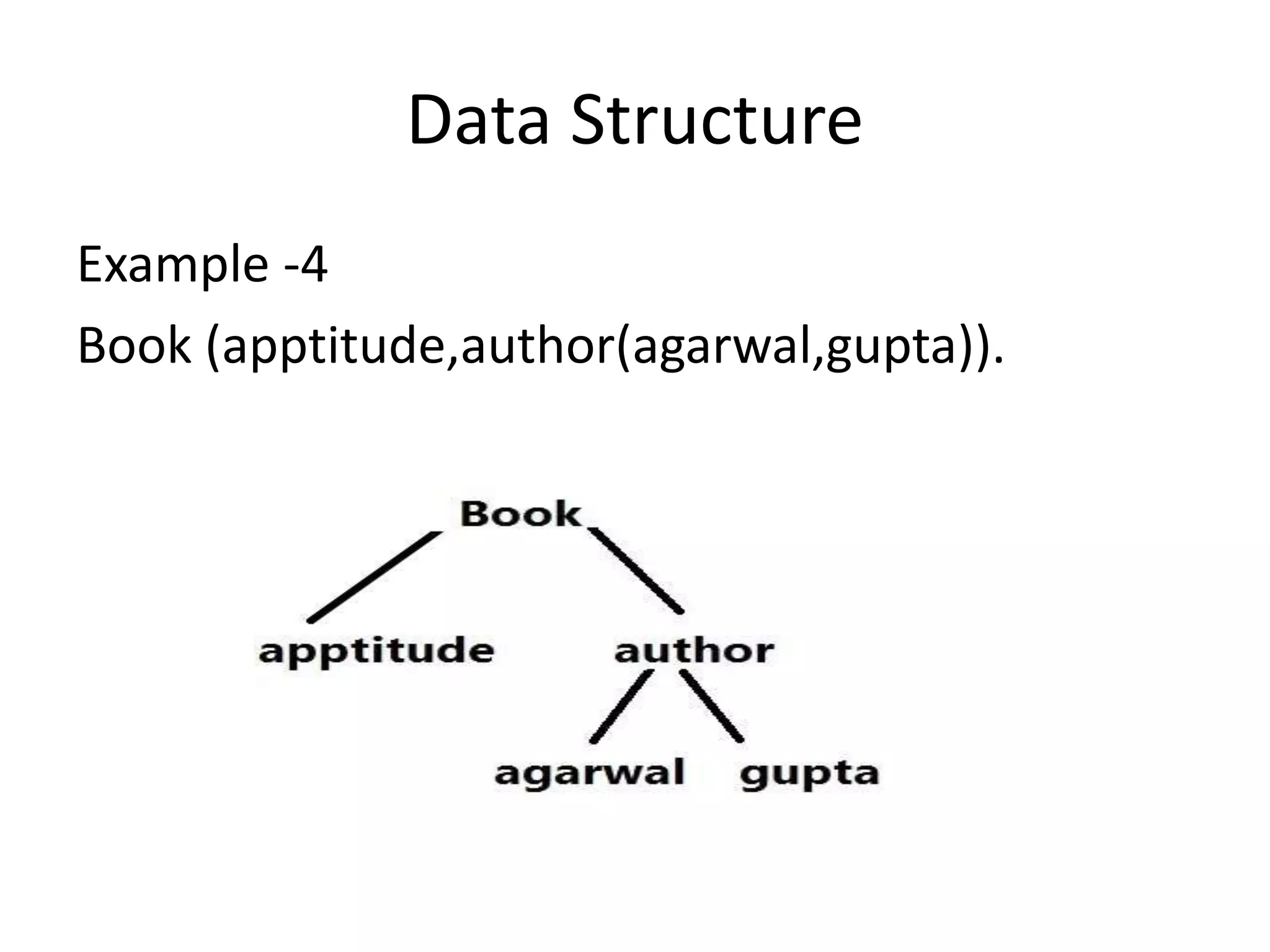
The document discusses propositional logic and provides examples of its data structures and applications. It explains that propositional logic can represent statements using variables and logical connectives like implication, conjunction, disjunction and negation. An example problem is given about a student's cleverness and passing that is translated into propositional logic statements. Backtracking is also discussed as a way to determine if a propositional logic sentence is satisfiable by searching for a solution. Some improvements to backtracking mentioned are the pure symbol heuristic and unit clause heuristic.

1. Propositional Logic

2. Propositional Logic Content
• Data Structure
• Examples
• Fact, Rules & Question
• Backtracking

3. Data Structure
• It Is Of Types
1) Structure & Tree
2) List
For Example :-
Student (ram,shyam,amit).

4. Data Structure
Example -2
Student (ram,roll_no(fine)).

5. Data Structure
Example -3
Student(pcet,cse (sixth(l), eighth (ll))).

6. Data Structure
Example -4
Book (apptitude,author(agarwal,gupta)).

7. Backtracking
Determine if an input propositional logic
sentence (in CNF) is
satisfiable. This is just backtracking search for a
CSP.
Improvements:
1. Early termination
A clause is true if any literal is true.
A sentence is false if any clause is false.

8. Examples
• Propositional logic Example
• The syntax of propositional logic is most easily introduced through an
example.
• Example
• A = { If I am clever then I will pass,
• If I will pass then I am clever,
• Either I am clever or I will pass }
• C = I am clever and I will pass
• The conclusion that I am clever and I will pass is a logical consequence of
the axioms. The example is written in English, but it is easily translated
into propositional logic. There are two propositions in the example: I am
clever and I will pass. In propositional logic, these propositions can be
represented by their text. Using the Prolog convention of starting
propositions with lowercase alphabetic, the axiom set and conclusion
become :

9. Examples
• A = { If i_am_clever then i_will_pass,
• If i_will_pass then i_am_clever,
• Either i_am_clever or i_will_pass }
• C = i_am_clever and i_will_pass
• To remove the if-then and other English words, connectives are used. The
commonly used connectives of propositional logic are:
• ~ for negation. This is "not" in English. Negation takes a single formula as
its argument, e.g., ~i_am_clever, and is thus a unary connective.
• ∧ or & for conjunction This is "and" in English. Conjunction is an infix
binary connective, taking two formulae as arguments, e.g., i_am_clever &
i_will_pass.
• ∨ or | for disjunction This is also known as "inclusive or", and corresponds
to some uses of "or" in English. Disjunction is also infix binary,
e.g., i_am_clever | i_will_pass.

10. Examples
• => for implication. This corresponds to the English if-then
construction. Implication is binary infix. The left hand operand is
called the antecedent, and the right hand operand is called the
consequent. E.g., i_am_clever => i_will_pass.
• <=> for equivalence. This is also known as double implication, and
has the meaning of "if and only if" in English. Equivalence is binary
infix, e.g., i_am_clever <=> i_will_pass.
• <~> for exclusive or. It has the meaning of "one or the other, but not
both" in English. Exclusive or is binary infix, e.g., democrat <~>
republican.
• There are other less common connectives, giving a total of four
unary connectives and 16 binary ones. Any good introductory text
on logic, e.g., [Chu56] will provide details. For ATP, the above are
adequate. The truth tables for the connectives provide their
meaning.

11. Backtracking
2. Pure symbol heuristic
Pure symbol: always appears with the same
"sign" in all clauses.
e.g., In the three clauses (A  B), (B 
C), (C  A), A and B are pure, C is impure.
Make a pure symbol literal true. (if there is a
model for S, then making a pure symbol
true is also a model).
3 Unit clause heuristic
Unit clause: only one literal in the clause
The only literal in a unit clause must be true.