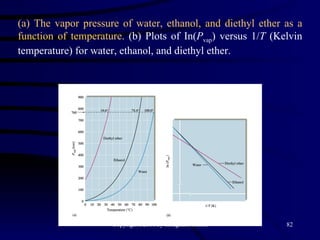
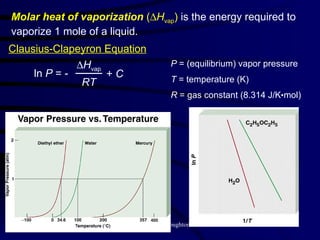
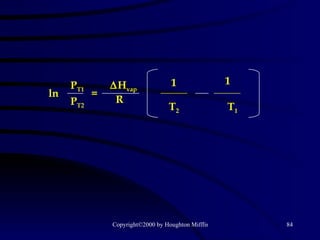
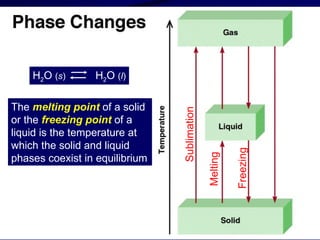
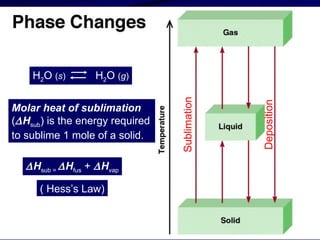
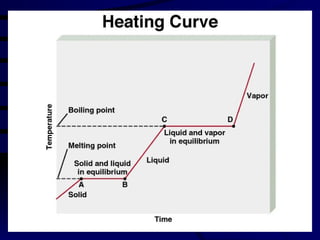
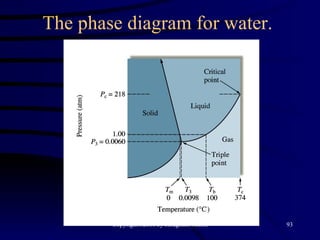
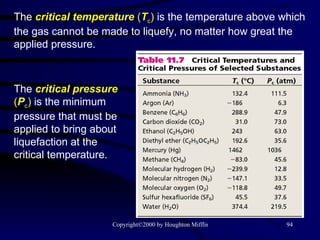
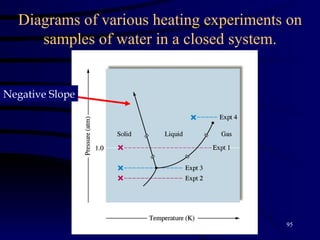
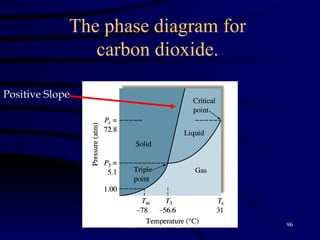
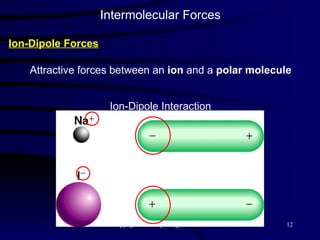
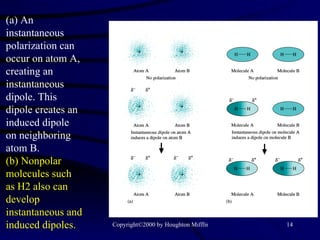
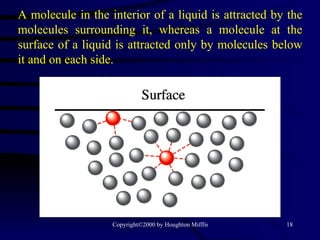
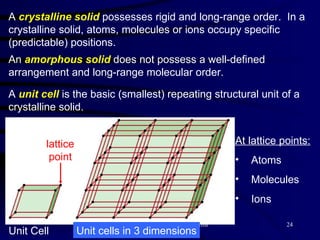
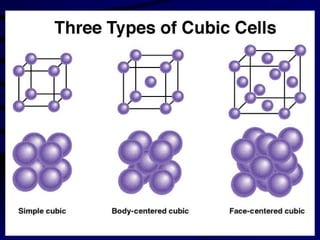
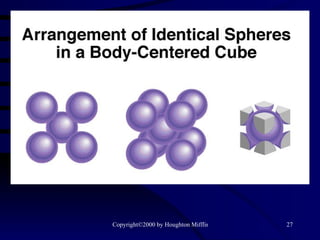
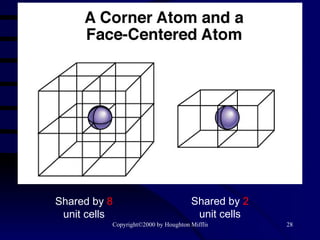
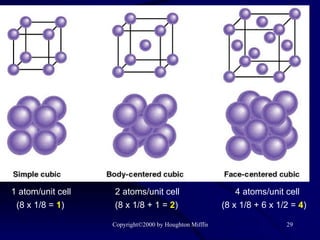
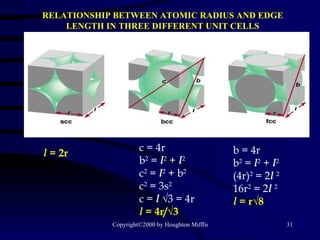
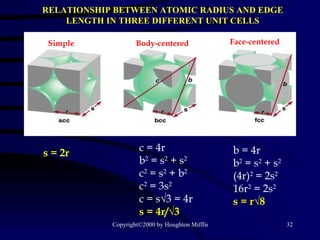
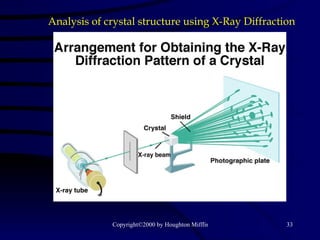
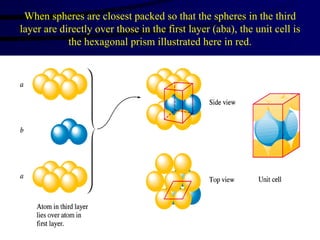
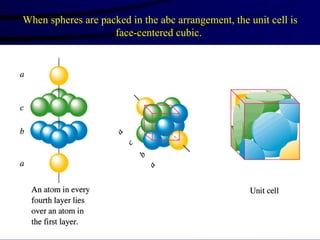
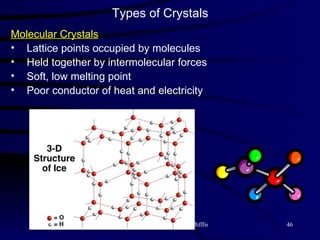
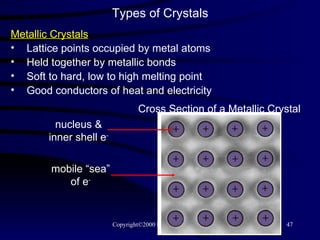
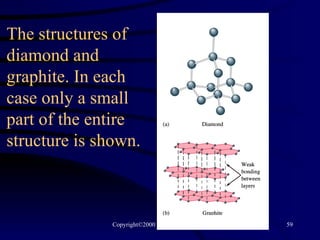
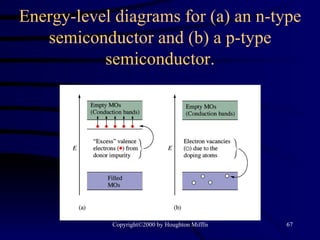
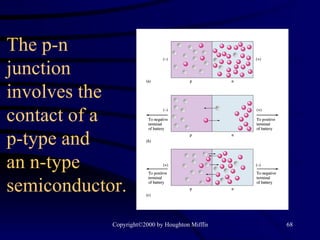
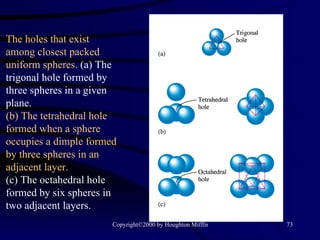
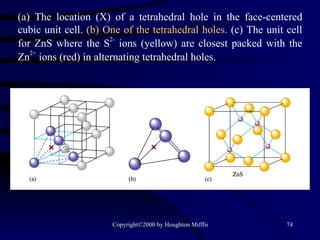
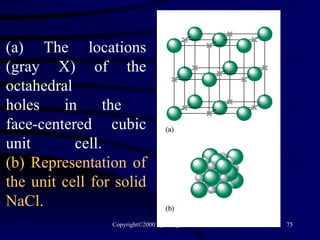
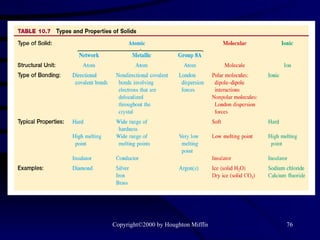
This document discusses different states of matter and properties of liquids and solids. It defines key terms like phases, intermolecular forces, and boiling point. It describes different types of solids like ionic, molecular, metallic and network solids. It also discusses properties of liquids like surface tension, capillary action, and viscosity.

1. Liquids and Solids Chapter 10

2. A phase is a homogeneous part of the system in contact with other parts of the system but separated from them by a well-defined boundary. 2 Phases Solid phase - ice Liquid phase - water

3. Schematic representations of the three states of matter.

5. Intermolecular Forces Intermolecular forces are attractive forces between molecules. Intramolecular forces hold atoms together in a molecule. Intermolecular vs Intramolecular 41 kJ to vaporize 1 mole of water ( inter ) 930 kJ to break all O-H bonds in 1 mole of water ( intra ) “ Measure” of intermolecular force boiling point melting point  H vap  H fus  H sub Generally, inter molecular forces are much weaker than intra molecular forces.

6. Intermolecular Forces Forces between (rather than within) molecules. dipole-dipole attraction : molecules with dipoles orient themselves so that “+” and “  ” ends of the dipoles are close to each other. hydrogen bonds : dipole-dipole attraction in which hydrogen is bonded to a highly electronegative atom ( F, O, N ).

7. Intermolecular Forces Dipole-Dipole Forces Attractive forces between polar molecules Orientation of Polar Molecules in a Solid

8. The electrostatic interaction of two polar molecules. (b) The interaction of many dipoles in a condensed state.

9. (a) The polar water molecule. (b) Hydrogen bonding among water molecules.

11. Why is the hydrogen bond considered a “special” dipole-dipole interaction? Why this sudden increase? The boiling point represents the magnitude and type of bonding Decreasing molar mass Decreasing boiling point

12. Intermolecular Forces Ion-Dipole Forces Attractive forces between an ion and a polar molecule Ion-Dipole Interaction

13. London Dispersion Forces relatively weak forces that exist among noble gas atoms and nonpolar molecules (Ar, sugar, C 8 H 18 ). caused by instantaneous dipole , in which electron distribution becomes asymmetrical. the ease with which electron “cloud” of an atom can be distorted is called polarizability .

14. (a) An instantaneous polarization can occur on atom A, creating an instantaneous dipole. This dipole creates an induced dipole on neighboring atom B. (b) Nonpolar molecules such as H2 also can develop instantaneous and induced dipoles.

15. Intermolecular Forces Dispersion Forces Continued Polarizability is the ease with which the electron distribution in the atom or molecule can be distorted. Polarizability increases with: greater number of electrons more diffuse electron cloud Dispersion forces usually increase with molar mass.

16. What type(s) of intermolecular forces exist between each of the following molecules? HBr HBr is a polar molecule: dipole-dipole forces. There are also dispersion forces between HBr molecules. CH 4 CH 4 is nonpolar: dispersion forces. SO 2 SO 2 is a polar molecule: dipole-dipole forces. There are also dispersion forces between SO 2 molecules. S O O

17. Properties of Liquids Surface tension is the amount of energy required to stretch or increase the surface of a liquid by a unit area. Or The resistance to an increase in its surface area ( polar molecules ). Strong intermolecular forces High surface tension

18. A molecule in the interior of a liquid is attracted by the molecules surrounding it, whereas a molecule at the surface of a liquid is attracted only by molecules below it and on each side.

19. More Properties of Liquids Capillary Action: Spontaneous rising of a liquid in a narrow tube. Nonpolar liquid mercury forms a convex meniscus in a glass tube, whereas polar water forms a concave meniscus.

20. More Properties of Liquids Cohesion is the intermolecular attraction between like molecules Adhesion is an attraction between unlike molecules Adhesion Cohesion

21. More Properties of Liquids Viscosity is a measure of a fluid’s resistance to flow. Strong intermolecular forces High viscosity

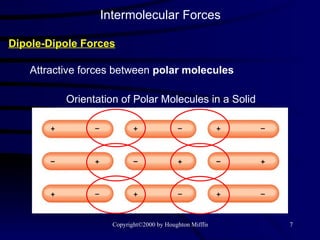
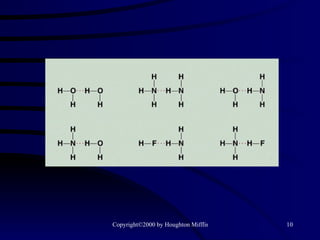
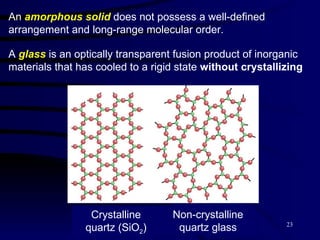
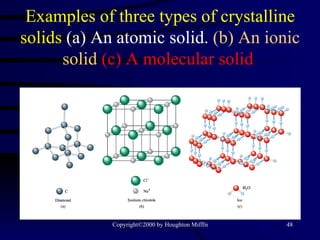
22. Types of Solids Crystalline Solids : highly regular arrangement of their components [ table salt (NaCl), pyrite (FeS 2 ) ]. Amorphous solids : considerable disorder in their structures ( glass ).

23. An amorphous solid does not possess a well-defined arrangement and long-range molecular order. A glass is an optically transparent fusion product of inorganic materials that has cooled to a rigid state without crystallizing Crystalline quartz (SiO 2 ) Non-crystalline quartz glass

24. A crystalline solid possesses rigid and long-range order. In a crystalline solid, atoms, molecules or ions occupy specific (predictable) positions. An amorphous solid does not possess a well-defined arrangement and long-range molecular order. A unit cell is the basic (smallest) repeating structural unit of a crystalline solid. Unit Cell At lattice points: Atoms Molecules Ions Unit cells in 3 dimensions lattice point

28. Shared by 8 unit cells Shared by 2 unit cells

29. 1 atom/unit cell (8 x 1/8 = 1 ) 2 atoms/unit cell (8 x 1/8 + 1 = 2 ) 4 atoms/unit cell (8 x 1/8 + 6 x 1/2 = 4 )

30. Three cubic unit cells and the corresponding lattices.

31. RELATIONSHIP BETWEEN ATOMIC RADIUS AND EDGE LENGTH IN THREE DIFFERENT UNIT CELLS l = 2r c = 4r b 2 = l 2 + l 2 c 2 = l 2 + b 2 c 2 = 3s 2 c = l √3 = 4r l = 4r/√3 b = 4r b 2 = l 2 + l 2 (4r) 2 = 2 l 2 16r 2 = 2 l 2 l = r√8

32. RELATIONSHIP BETWEEN ATOMIC RADIUS AND EDGE LENGTH IN THREE DIFFERENT UNIT CELLS s = 2r c = 4r b 2 = s 2 + s 2 c 2 = s 2 + b 2 c 2 = 3s 2 c = s√3 = 4r s = 4r/√3 b = 4r b 2 = s 2 + s 2 (4r) 2 = 2s 2 16r 2 = 2s 2 s = r√8 Simple Body-centered Face-centered

33. Analysis of crystal structure using X-Ray Diffraction

34. BC + CD = 2 d sin  = n  (Bragg Equation) Extra distance =

35. Bragg Equation Used for analysis of crystal structures. n  = 2 d sin  d = distance between atoms n = an integer  = wavelength of the x-rays

36. X rays of wavelength 0.154 nm are diffracted from a crystal at an angle of 14.17 0 . Assuming that n = 1, what is the distance (in pm) between layers in the crystal? n  = 2 d sin  n = 1  = 14.17 0  = 0.154 nm = 154 pm d = = 77.0 pm 11.5 n  2sin  = 1 x 154 pm 2 x sin14.17

37. Types of Crystalline Solids Ionic Solid : contains ions at the points of the lattice that describe the structure of the solid ( NaCl ). Molecular Solid : discrete covalently bonded molecules at each of its lattice points ( sucrose , ice ).

38. Types of Crystals Ionic Crystals Lattice points occupied by cations and anions Held together by electrostatic attraction Hard, brittle, high melting point Poor conductor of heat and electricity CsCl ZnS CaF 2

39. Types of Crystals Atomic Crystals Lattice points occupied by atoms Held together by covalent bonds Hard, high melting point Poor conductor of heat and electricity diamond graphite carbon atoms

40. Packing in Metals Model : Packing uniform, hard spheres to best use available space. This is called closest packing . Each atom has 12 nearest neighbors. hexagonal closest packed (“aba”) cubic closest packed (“abc”)

41. The closest packing arrangement of uniform spheres, (a) aba packing (b) abc packing.

42. When spheres are closest packed so that the spheres in the third layer are directly over those in the first layer (aba), the unit cell is the hexagonal prism illustrated here in red.

43. When spheres are packed in the abc arrangement, the unit cell is face-centered cubic.

44. The indicated sphere has 12 nearest neighbors.

45. When silver crystallizes, it forms face-centered cubic cells. The unit cell edge length is 409 pm. Calculate the density of silver. V = a 3 = (409 pm) 3 = 6.83 x 10 -23 cm 3 4 atoms/unit cell in a face-centered cubic cell m = 4 Ag atoms = 7.17 x 10 -22 g = 10.5 g/cm 3 d = m V 107.9 g mole Ag x 1 mole Ag 6.022 x 10 23 atoms x d = m V 7.17 x 10 -22 g 6.83 x 10 -23 cm 3 =

46. Types of Crystals Molecular Crystals Lattice points occupied by molecules Held together by intermolecular forces Soft, low melting point Poor conductor of heat and electricity

47. Types of Crystals Metallic Crystals Lattice points occupied by metal atoms Held together by metallic bonds Soft to hard, low to high melting point Good conductors of heat and electricity Cross Section of a Metallic Crystal nucleus & inner shell e - mobile “sea” of e -

48. Examples of three types of crystalline solids (a) An atomic solid. (b) An ionic solid (c) A molecular solid

49. Types of Crystals

51. Bonding Models for Metals Electron Sea Model : A regular array of metals in a “sea” of electrons. Band (Molecular Orbital) Model: Electrons assumed to travel around metal crystal in MOs formed from valence atomic orbitals of metal atoms.

52. The electron sea model for metals postulates a regular array of cations in a "sea" of valence electrons. (a) Representation of an alkali metal (Group 1A) with one valence electron. (b) Representation of an alkaline earth metal (Group 2A) with two valence electrons.

53. The molecular orbital energy levels produced when various numbers of atomic orbitals interact.

54. (left) A representation of the energy levels (bands) in a magnesium crystal. (right) Crystals of magnesium grown from a vapor.

55. Metal Alloys 1. Substitutional Alloy : some metal atoms replaced by others of similar size. brass = Cu/Zn Substances that have a mixture of elements and metallic properties.

56. Metal Alloys (continued) 2. Interstitial Alloy : Interstices (holes) in closest packed metal structure are occupied by small atoms. steel = iron + carbon 3. Both types : Alloy steels contain a mix of substitutional (carbon) and interstitial (Cr, Mo) alloys.

57. Two types of alloys: (a) substitutional (b) interstitial

58. Network Solids Composed of strong directional covalent bonds that are best viewed as a “giant molecule”. brittle do not conduct heat or electricity carbon, silicon-based graphite, diamond, ceramics, glass

59. The structures of diamond and graphite. In each case only a small part of the entire structure is shown.

60. Partial representation of the molecular orbital energies in (a) diamond and (b) a typical metal.

61. The p orbitals (a) perpendicular to the plane of the carbon ring system in graphite can combine to form (b) an extensive π-bonding network.

62. Graphite consists of layers of carbon atoms.

63. Computer-generated model of silica.

64. (top) The structure of quartz (empirical formula SiO2). Quartz contains chains of SiO4 tetrahedral (bottom) that share oxygen atoms.

65. Semiconductors Conductivity is enhanced by doping with group 3a or group 5a elements. A substance in which some electrons can cross the band gap.

66. (a) A silicon crystal doped with arsenic, which has one more valence electron than silicon. (b) A silicon crystal doped with boron, which has one less electron than silicon.

67. Energy-level diagrams for (a) an n-type semiconductor and (b) a p-type semiconductor.

68. The p-n junction involves the contact of a p-type and an n-type semiconductor.

69. Molecular Solids Discrete molecular units at each lattice position e.g. ice, solid CO 2 , S 8 , P 4 . Covalent bond within molecule while weak dipole-dipole or London dispersion forces (LD) e.g. Ice (Hydrogen bond), CO 2 , P 4 , S 8 (LD) very reactive. As the size of the molecule increases, the LD become large causing many substances to be solids at 25 0 C.

70. A “steaming” piece of dry ice CO 2

71. (a) Sulfur crystals (yellow) contain S 8 molecules. (b) White phosphorus (containing P 4 molecules) is so reactive with the oxygen in air that it must be stored under water.

72. Ionic Solids Ionic solids are stable, high melting point and held ions together by strong electrostatic forces between opposite ions. Structure of most binary ionic solids (NaCl) can be explained by the closest packing of spheres Anion (large ion) packed in one of the closest packing (hcp or ccp) Cation (small ion) fits in holes among the anions.

73. The holes that exist among closest packed uniform spheres. (a) The trigonal hole formed by three spheres in a given plane. (b) The tetrahedral hole formed when a sphere occupies a dimple formed by three spheres in an adjacent layer. (c) The octahedral hole formed by six spheres in two adjacent layers.

74. (a) The location (X) of a tetrahedral hole in the face-centered cubic unit cell. (b) One of the tetrahedral holes. (c) The unit cell for ZnS where the S 2- ions (yellow) are closest packed with the Zn 2+ ions (red) in alternating tetrahedral holes.

75. (a) The locations (gray X) of the octahedral holes in the face-centered cubic unit cell. (b) Representation of the unit cell for solid NaCl.

77. Vapor Pressure . . . is the pressure of the vapor present at equilibrium . . . . is determined principally by the size of the intermolecular forces in the liquid. . . . increases significantly with temperature. Volatile liquids have high vapor pressures.

78. Behavior of a liquid in a closed container.

79. The equilibrium vapor pressure is the vapor pressure measured when a dynamic equilibrium exists between condensation and evaporation H 2 O ( l ) H 2 O ( g ) Rate of condensation Rate of evaporation = Dynamic Equilibrium

80. Before Evaporation At Equilibrium

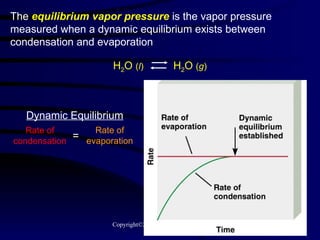
81. (a) The vapor pressure of a liquid can be measured easily using a simple barometer of the type shown here. (b) The three liquids, water, ethanol (C 2 H 5 OH), and diethyl ether [(C 2 H 5 ) 2 O], have quite different vapor pressures.

82. (a) The vapor pressure of water, ethanol, and diethyl ether as a function of temperature. (b) Plots of In( P vap ) versus 1/ T (Kelvin temperature) for water, ethanol, and diethyl ether.

83. Molar heat of vaporization (  H vap ) is the energy required to vaporize 1 mole of a liquid. P = (equilibrium) vapor pressure T = temperature (K) R = gas constant (8.314 J/K • mol) ln P = -  H vap RT + C Clausius-Clapeyron Equation

84. ln P T1 P T2 =  H vap R 1 1 T 2 T 1

85. The boiling point is the temperature at which the (equilibrium) vapor pressure of a liquid is equal to the external pressure. The normal boiling point is the temperature at which a liquid boils when the external pressure is 1 atm.

86. Melting Point Molecules break loose from lattice points and solid changes to liquid. (Temperature is constant as melting occurs.) vapor pressure of solid = vapor pressure of liquid

87. Melting 11.8 Freezing The melting point of a solid or the freezing point of a liquid is the temperature at which the solid and liquid phases coexist in equilibrium Sublimation H 2 O ( s ) H 2 O ( l )

88. Molar heat of fusion (  H fus ) is the energy required to melt 1 mole of a solid substance.

89. The supercooling of water. The extent of supercooling is given by S .

90. Sublimation Deposition  H sub =  H fus +  H vap ( Hess’s Law) Molar heat of sublimation (  H sub ) is the energy required to sublime 1 mole of a solid. H 2 O ( s ) H 2 O ( g )

92. Phase Diagram Represents phases as a function of temperature and pressure. critical temperature : temperature above which the vapor can not be liquefied. critical pressure : pressure required to liquefy AT the critical temperature. critical point : critical temperature and pressure (for water, T c = 374°C and 218 atm).

93. The phase diagram for water.

94. The critical temperature ( T c ) is the temperature above which the gas cannot be made to liquefy, no matter how great the applied pressure. The critical pressure ( P c ) is the minimum pressure that must be applied to bring about liquefaction at the critical temperature.

95. Diagrams of various heating experiments on samples of water in a closed system. Negative Slope

96. The phase diagram for carbon dioxide. Positive Slope