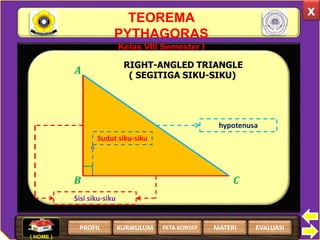
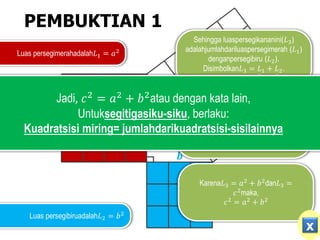
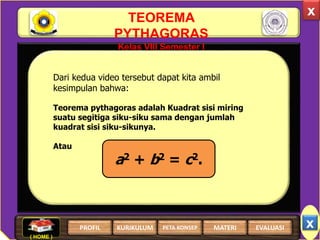
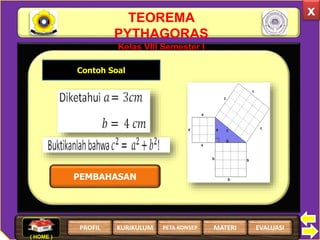
Dokumen tersebut membahas tentang Teorema Pythagoras, termasuk pengertian, pembuktian, contoh soal dan penyelesaiannya, serta evaluasi. Teorema Pythagoras menyatakan hubungan antara panjang sisi-sisi segitiga siku-siku, yaitu kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi lainnya.

5. ARE YOU
READY????
START

6. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
TEOREMA PYTHAGORAS
Kelas VIII Semester I
x
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

7. PROFIL
Nama :Rya Agustini
TTL : Palembang, 14 Agustus 1996
Alamat : Jl. Tanjung Rawo Lorong Pos No. 48C
RT 53 RW 16 Bukit Lama Palembang
PENDIDIKAN MATEMATIKA
UNIVERSITAS SRIWIJAYA
ryaagustini1408@gmail.com Rya Agustini
Ryayayak Ryayayak
x
OR
Check This
Out
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

8. ( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP
x

9. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
1. Menghargai dan menghayati ajaran agama yang dianutnya
2. Menghargai dan menghayati perilaku jujur, disiplin, tanggungjawab,
peduli (toleransi, gotong royong), santun, percaya diri, dalam
berinteraksi secara efektif dengan lingkungan sosial dan alam dalam
jangkauan pergaulan dan keberadaannya
3. Memahami pengetahuan (faktual, konseptual, dan prosedural)
berdasarkan rasa ingin tahunya tentang ilmu pengetahuan, teknologi,
seni, budaya terkait fenomena dan kejadian tampak mata
4. Mencoba mengolah, dan menyaji dalam ranah konkret (menggunakan,
mengurai, merangkai, memodifikasi, dan membuat) dan ranah abstrak
(menulis, membaca, menghitung, menggambar, dan mengarang)
sesuai dengan yang dipelajari di sekolah dan sumber lain yang sama
dalam sudut pandang/teori
x
KOMPETENSI INTI
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

10. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
1. Memahami Teorema Pythagoras melalui alat peraga dan
penyelidikan pola bilangan.
2. MenggunakanTeorema Pythagoras untuk menyelesaikan
berbagai masalah.
3. Menggunakan pola dan generalisasi untuk
menyelesaikan masalah nyata.
x
KOMPETENSI DASAR
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

11. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
Setelah mempelajari materi ini, diharapkan siswa mampu:
1. Menemukan Teorema Pythagoras dengan menggunakan
alat peraga dan pola bilangan
2. Menemukan hubungan antar sisi pada segitiga siku-siku
khusus.
3. Menyelesaikan permasalaha nyata dengan Teorema
Pythagoras.
x
TUJUAN PEMBELAJARAN
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

12. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
PETA KONSEP
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

13. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
Siapakah Pythagoras itu?
x
PENGERTIAN TEOREMA PYTHAGORAS
Pythagoras adalah seorang ahli
matematika dan filsafat berkebangsaan
Yunani yang hidup pada tahun 569 –
475 sebelum Masehi.
Teorema Pythagoras sendiri artinya :
Teorema yang menunjukkan
hubungan panjang sisi-sisi pada
segitiga siku-siku.
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

14. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
RIGHT-ANGLED TRIANGLE
( SEGITIGA SIKU-SIKU)
Sisi siku-siku
hypotenusa
Sudut siku-siku
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

15. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
Kuadrat panjang sisi
miring suatu segitiga siku-
siku adalah
sama dengan jumlah
kuadrat panjang sisi - sisi
yang lain.
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

16. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
Theorem I (Pythagoras’ Theorem)
For a right-angled with two legs a, b, and hypotenuse c, the sum of
squares of legs is equal to the square of its hypotenuse,
a2 + b2 = c2.
Theorem II (Inverse Theorem)
If the lengths a, b, c of three sides of a triangle have the relation a2
+ b2 = c2, then the triangle must be a right-angled triangle with
two legs a, b, and hypotenuse c.
x
PYTHAGOREAN THEOREM
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

17. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
Teorema I (Pythagoras 'Teorema)
Untuk siku-siku dengan dua sisi a, b, dan sisi miring c,
jumlah kuadrat dari dua sisi tersebut tersebut adalah sama
dengan kuadrat sisi miringnya, a2 + b2 = c2.
Teorema II (Inverse teorema)
Jika panjang a, b, c dari tiga sisi segitiga memiliki
hubungana2 + b2 = c2 ,maka segitiga itu pasti segitiga siku-
siku dengan dua kaki a, b, dan sisi miring c.
x
TEOREMA PYTHAGORAS
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

18. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
MENEMUKAN TEOREMA PYTHAGORAS
PEMBUKTIAN 1
PEMBUKTIAN 2
VIDEO
PEMBUKTIAN 1
VIDEO
PEMBUKTIAN 2
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

19. PEMBUKTIAN 1
𝒂
𝒃
𝒄
Luas persegimerahadalah𝐿1 = 𝑎2
Luas persegibiruadalah𝐿2 = 𝑏2
Sehingga luaspersegikananini(𝐿3)
adalahjumlahdariluaspersegimerah (𝐿1)
denganpersegibiru (𝐿2).
Disimbolkan𝐿3 = 𝐿1 + 𝐿2.
Diperoleh𝐿3 = 𝑎2
+ 𝑏2
.
Padahal
persegikananiniadalahsuatupersegi
yang memilikipanjangsisi𝑐.
Sehinggaluasnyaadalah𝐿3 = 𝑐2.
Karena𝐿3 = 𝑎2 + 𝑏2dan𝐿3 =
𝑐2
maka,
𝑐2 = 𝑎2 + 𝑏2
Jadi, 𝑐2 = 𝑎2 + 𝑏2atau dengan kata lain,
Untuksegitigasiku-siku, berlaku:
Kuadratsisi miring= jumlahdarikuadratsisi-sisilainnya
x

20. PEMBUKTIAN 2
𝒂
𝒃
𝒂
𝒂
𝒂
𝒃
𝒃
𝒃
𝒄
𝒄
𝒄
𝒄
Perhatikan gambar di samping.
Keempatsegitigasiku-siku di
sampingmemilikiukuransisi-sisi yang sama,
yaitu𝑎, 𝑏,dan𝑐
Dapatkah kalian menghitung luas persegi abu-
abu di samping?
Ya, luaspersegiabu-abu di sampingadalah𝐿 =
𝑐2
.
Sekarang, apakah luas persegi abu-abu tadi
sama dengan luas daerah abu-abu sekarang?
Mengapa?
Padahal luasdaerahabu-
abusekarangadalah𝐿 = 𝑎2 + 𝑏2. Mengapa?
Jadi, 𝑐2
= 𝑎2
+ 𝑏2
.
Jadiuntuksegitigasiku-siku:
Kuadratsisi miring = jumlahkuadratsisi-sisilainnya
(𝑐2 = 𝑎2 + 𝑏2).
Dari gambar yang sama. Silahkan Anda buktikan
dengan cara yang lain.
x

21. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
VIDEO PEMBUKTIAN 1
x
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

22. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
PEMBUKTIAN 2
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

23. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
Dari kedua video tersebut dapat kita ambil
kesimpulan bahwa:
Teorema pythagoras adalah Kuadrat sisi miring
suatu segitiga siku-siku sama dengan jumlah
kuadrat sisi siku-sikunya.
Atau
a2 + b2 = c2.
x
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

24. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
MENENTUKAN TEOREMA PYTHAGORAS
Perhatikan gambar disamping!
Segitiga siku-siku mempunyai sebuah
persegi pada setiap sisinya. Persegi
pada hipotenusa merupakan persegi
terbesar.
Hubungan ketiga persegi itu disebut
Teorema Pythagoras, yaitu:
Pada sebuah segitiga siku-siku selalu berlaku:
Kuadrat dari sisi terpanjang= jumlah kuadrat
dari dua sisi lainnya.
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

25. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
Contoh Soal
PEMBAHASAN
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

26. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
Berdasarkan pernyataan:
Pada sebuah
segitiga siku-siku
selalu berlaku:
Kuadrat dari sisi
terpanjang=
jumlah kuadrat
dari dua sisi
lainnya.
MAKA
JAWAB:
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

27. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
Sebuah kapal berlayar 10 km ke arah selatan
dan dilanjutkan ke arah garat sejauh 8,5 km.
Hitunglah jauh kapal itu berlayar dari titik
awal jika ditarik garis lurus?
PENERAPAN TEOREMA PYTHAGORAS
Contoh:
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP
PEMBAHASAN

28. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
Jawab:
Buatlah skema dari soal tersebut.
Perhatikan gambar di samping!
Misalnya a=10 km, b=8,5 km.
Maka berdasarkan Teorema Pythagoras
diperoleh:
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

29. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
EVALUASI
ENGLISH
INDONESIAN
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

30. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
EVALUASI
1. Find the length of BC
2. A ladder leans against a vertical wall. The length of the ladder
is 5 m. The foot of the ladder is 2 m from the base of the wall.
How high is the top of the ladder above the ground?
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

31. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
EVALUASI
3. Tiara runs diagonally across
a rectangular field that has a
length of 40 yards and a width
of 30 yards, as shown in the
diagram.
What is the length of the
diagonal, in yards, that Tiara
runs?
x
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

32. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
EVALUASI
1.Carilah panjang BC
2. Sebuah tangga bersandar dinding vertikal. Panjang tangga
adalah 5 m. Kaki tangga adalah 2 m dari dasar dinding.
Seberapa tinggi puncak tangga di atas tanah?
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP

33. TEOREMA
PYTHAGORAS
Kelas VIII Semester I
x
EVALUASI
3. Tiara berjalan diagonal di bidang
segi empat yang memiliki
panjang 40 kilometer dan lebar
30 kilometer, seperti yang
ditunjukkan dalam diagram.
Berapa panjang diagonal, di
halaman, yang Tiara lewati?
x
( HOME )
PROFIL EVALUASIMATERIKURIKULUM PETA KONSEP