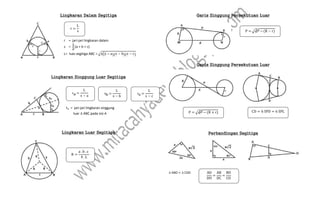
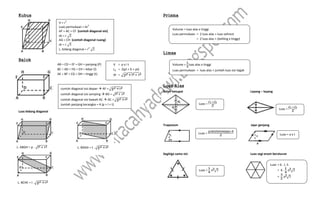
Dokumen ini menjelaskan konsep dan langkah-langkah untuk menggambar lingkaran luar dan dalam segitiga, beserta berbagai rumus matematika yang terkait dengan segitiga dan lingkaran. Selain itu, juga dibahas mengenai volume dan luas permukaan berbagai bangun ruang seperti kubus dan balok. Informasi penting lainnya mencakup hubungan antara sisi segitiga dan jari-jari lingkaran yang berkaitan.

1. Lingkaran
Keterangan : d = diameter
r = jari-jari
 KBusurP 0
360
.

Segitiga
Sudut Pusat dan Sudut Keliling
Sudut yang menghadap busur yang sama besarnya sama.

2. Sudut Dalam dan Luar Keliling Lingkaran
Segiempat Tali Busur
Dalil Ptolemius
Potongan – Potongan Tali Busur Lingkaran
Melukis Lingkaran Luar Segitiga
Langkah-langkah:
a. Buatlah garis sumbu pada kedua sisi segitiga.
 Garis sumbu : garis yang melalui titik tengah suatu sisi segitiga dan tegak lurus terhadap
sisi segitiga.
b. Titik potong kedua garis sumbu tersebut merupakan titik pusat lingkaran luar segitiga.
c. Jari-jari lingkaran luar segitiga tersebut adalah jarak antara titik pusat lingkaran dengan sudut
segitiga.
Melukis Lingkaran Dalam Segitiga
Langkah-langkah:
a. Buatlah garis bagi pada dua sudut segitiga.
 Garis bagi : garis yang membagi sudut segitiga menjadi dua sama besar.
b. Titik potong kedua garis bagi tersebut merupakan titik pusa lingkaran dalam segitiga.
c. Buat garis tegak lurus sisi melalui titik pusat lingkaran tersebut.
d. Jari-jari lingkaran dalam segitiga tersebut adalah jarak antara titik pusat lingkaran dengan titik
potong garis tegak lurus sisi.

3. Lingkaran Dalam Segitiga
Lingkaran Singgung Luar Segitiga
Lingkaran Luar Segitiga
Garis Singgung Persekutuan Luar
Garis Singgung Persekutuan Luar
Perbandingan Segitiga
 ABO   CDO
r =
L
s
r = jari-jari lingkaran dalam
s = (a + b + c)
L= luas segitiga ABC = s(s − a)(s − b)(s − c)
r =
L
s − a
ra = jari-jari lingkaran singgung
luar  ABC pada sisi A
r =
L
s − b
r =
L
s − c
R =
a . b . c
4 . L
P = d − (R − r)
AO
DO
=
AB
DC
=
BO
CO
P = d − (R + r) CD = 6 SPD = 6 SPL

4. V = p x l t
Lp = 2(pl + lt + pt)
dr = p + l + t
Kubus
Balok
Luas bidang diagonal
Prisma
Limas
Luas Alas
Belah ketupat Layang – layang
Trapesium Jajar genjang
Segitiga sama sisi Luas segi enam beraturan
V = r
3
Luas permukaan = 6r
3
AF = AC = CF (contoh diagonal sisi)
ds = r √2
AG = CH (contoh diagonal ruang)
dr = r √3
L. bidang diagonal = r
2
√2
Luas =
×
Luas = ( )×
Luas = a x t
Luas = a √3
Luas =
×
Luas = 6 . L 
= 6 . a √3
= a √3
Volume = luas alas x tinggi
Luas permukaan = 2 luas alas + luas selimut
= 2 luas alas + (keliling x tinggi)
Volume = luas alas x tinggi
Luas permukaan = luas alas + jumlah luas sisi tegak
L. ABGH = p . √l + t
L. BCHE = l . p + t
L. BDGH = t . p + l
AB = CD = EF = GH = panjang (P)
BC = AD = FG = EH = lebar (l)
AE = BF = CG = DH = tinggi (t)
contoh diagonal sisi depan  AF = p + t
contoh diagonal sisi samping  BG = √l + t
contoh diagonal sisi bawah AC  AC = p + l
Jumlah panjang kerangka = 4 (p + l + t)