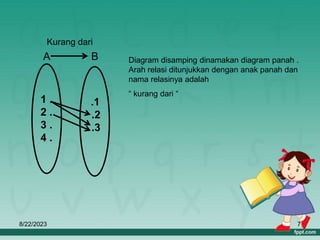
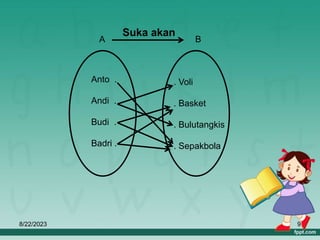
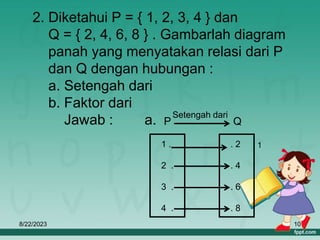
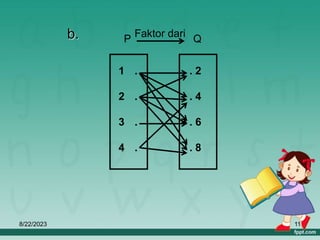
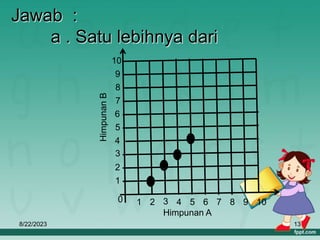
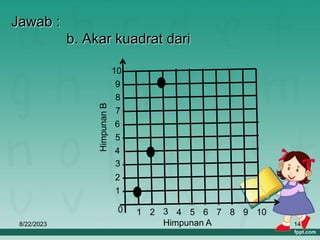
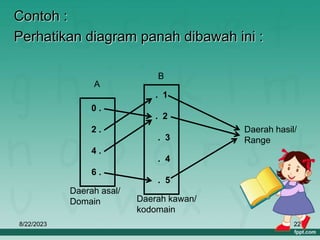
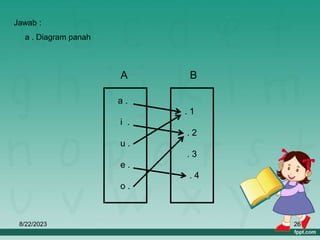
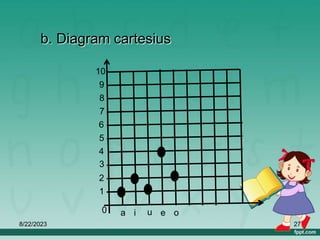
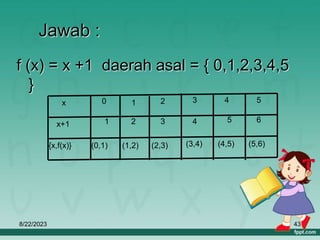
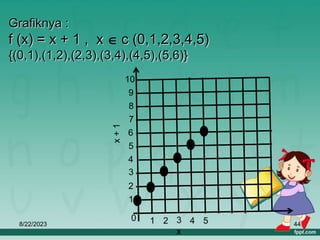
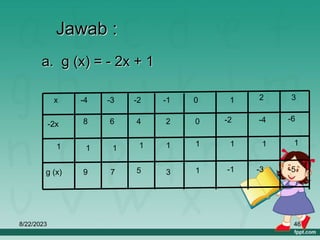
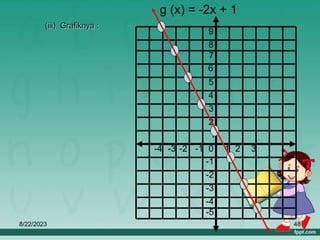
Dokumen ini membahas tentang relasi dan fungsi dalam matematika, termasuk cara menyatakan relasi menggunakan diagram panah, diagram cartesius, dan himpunan pasangan berurutan. Selain itu, dijelaskan juga pengertian fungsi serta bagaimana cara memetakan anggota himpunan dengan tepat. Materi ini bertujuan untuk memudahkan pemahaman tentang pengelompokan dan hubungan antar himpunan.

1. Relasi dan Fungsi

2. Apersepsi
Dapatkah kamu menyebutkan contoh suatu relasi!

3. Motivasi

4. Tujuan Pembelajaran
• Menyatakan relasi dalam bentuk diagram
panah
• Menyatakan relasi dalam bentuk diagram
Cartesius
• Menyatakan relasi dalam bentuk
himpunan pasangan berurutan

5. Manfaat Mempelajari Relasi
Dengan mempelajari Relasi kita dapat
mengelompokkan sesuatu dengan
mudah sesuai aturan yang dikehendaki

6. 8/22/2023 6
A. RELASI
1. Pengertian Relasi
Relasi ( hubungan ) dari himpunan A ke B
adalah pemasangan anggota-anggota A
dengan anggota-anggota B.
Relasi dalam matematika misalnya : lebih
dari , kurang dari , setengah dari , faktor dari
, dan sebagainya .
Contoh :
Diketahui A = { 1, 2, 3, 4 } dan B = { 1, 2, 3 }
. Jika
himpunan A ke himpunan B dinyatakan
relasi “ kurang dari “ , maka lebih jelasnya
dapat ditunjukkan pada gambar di bawah :

7. 8/22/2023 7
Diagram disamping dinamakan diagram panah .
Arah relasi ditunjukkan dengan anak panah dan
nama relasinya adalah
“ kurang dari “
1 .
2 .
3 .
4 .
.1
.2
.3
B
A
Kurang dari

8. 8/22/2023 8
2. Menyatakan Relasi
Relasi antara dua himpunan dapat dinyatakan dengan 3
cara , yaitu : Diagram Panah , Diagram Cartesius , dan
Himpunan pasangan berurutan .
a. Diagram Panah
Contoh :
1. Jika Anto suka sepakbola , Andi suka voli
dan bulutangkis serta Budi dan Badri suka
basket dan sepakbola . Buatlah Diagram
Panah keadaan tersebut apabila A adalah
himpunan anak dan B adalah himpunan
olahraga .

9. 8/22/2023 9
. Voli
. Basket
. Bulutangkis
. Sepakbola
Anto .
Andi .
Budi .
Badri .
B
A
Suka akan

10. 8/22/2023 10
2. Diketahui P = { 1, 2, 3, 4 } dan
Q = { 2, 4, 6, 8 } . Gambarlah diagram
panah yang menyatakan relasi dari P
dan Q dengan hubungan :
a. Setengah dari
b. Faktor dari
Jawab : a.
1
. 2
. 4
. 6
. 8
1 .
2 .
3 .
4 .
Q
P
Setengah dari

11. 8/22/2023 11
b.
. 2
. 4
. 6
. 8
1 .
2 .
3 .
4 .
Q
P
Faktor dari

12. 8/22/2023 12
b. Diagram
Cartesius
Contoh :
Diketahui A = { 1, 2, 3, 4, 5 } dan
B = { 1, 2, 3, …, 10 }.
Gambarlah diagram cartesius yang
menyatakan relasi A ke B dengan
hubungan :
a. Satu lebihnya dari
b. Akar kuadrat dari

13. 8/22/2023 13
Jawab :
a . Satu lebihnya dari
1
1 2 3 4 5 6 7 9
8 10
0
2
3
4
5
6
7
8
9
10
Himpunan
B
Himpunan A

14. 8/22/2023 14
Jawab :
b. Akar kuadrat dari
1
1 2 3 4 5 6 7 9
8 10
0
2
3
4
5
6
7
8
9
10
Himpunan
B
Himpunan A

15. 8/22/2023 15
C. Himpunan pasangan
berurutan
Contoh :
Himpunan A = { 1, 2, 3, … , 25} dan
B = { 1, 2, 3, … , 10 } .
Tentukan himpunan pasangan berurutan yang
menyatakan relasi A ke B dengan hubungan :
a. kuadrat dari
b. dua kali dari
c. Satu kurangnya dari

16. 8/22/2023 16
Jawab :
a. { (1,1), (4,2), (9,3),(16,4), (25,5) }
b. { (2,1), (4,2), (6,3), (8,4), (10,5), (12,6),
(14,7),(16,8), (18,9),(20,10) }
c. { (1,2) , (2,3), (3,4), (4,5), (5,6), (6,7),
(7,8), (8,9), (9,10) }

17. Silahkan Bentuk Kelompok!
Buka LKPD masing-masing, Jika ada
pertanyaan, acungkan tanganmu, agar
kelompok lain bisa mendengarkan
bersama!

18. Refleksi
Bagaimana pembelajaran hari ini?
Apa yang kamu ketahui?
Adakah yang belum kamu pahami?

19. Kesimpulan
Relasi antara dua himpunan dapat dinyatakan
dengan 3 cara , yaitu : Diagram Panah , Diagram
Cartesius , dan Himpunan pasangan berurutan

20. EVALUASI
1. Kerjakan tugas Uji Kompetensi 1 di
BUPENA!

21. 8/22/2023 21
B.
FUNGSI
1. Pengertian Fungsi
Sebuah fungsi f : x  y adalah suatu aturan yang
memasangkan tiap anggota x pada suatu himpunan
(daerah asal / domain), dengan tepat sebuah nilai y dari
himpunan kedua (daerah kawan / kodomain). Himpunan
nilai yang diperoleh disebut daerah hasil / range fungsi
tersebut .
Untuk lebih memahami pengertian diatas perhatikan contoh
berikut :

22. 8/22/2023 22
Contoh :
Perhatikan diagram panah dibawah ini :
. 1
. 2
. 3
. 4
. 5
0 .
2 .
4 .
6 .
B
A
Daerah kawan/
kodomain
Daerah asal/
Domain
Daerah hasil/
Range

23. 8/22/2023 23
Dari diagram panah diatas dapat dilihat bahwa
:
1. Fungsi A ke B adalah relasi khusus yang
memasangkan setiap anggota A dengan
tepat satu anggota B.
2. Himpunan A = { 0, 2, 4, 6 } disebut daerah
asal ( Domain ), Himpunan B = { 1, 2, 3, 4,
5 }
disebut daerah kawan ( Kodomain ), dan
{ 1, 2, 5 } disebut daerah hasil ( Range ).

24. 8/22/2023 24
2. Notasi Fungsi
Fungsi/ pemetaan dapat dinotasikan
dengan huruf kecil f , g , h , dan
sebagainya.
Misal :
f : x  y dibaca f memetakkan x ke y ,
maka
y = f(x) dibaca sama dengan f dari x
digunakan untuk menunjukkan bahwa y
adalah fungsi dari x .

25. 8/22/2023 25
Suatu fungsi juga dapat dinyatakan dengan tiga
cara yaitu dengan diagram panah , diagram
cartesius , dan himpunan pasangan berurutan .
Contoh :
Diketahui A = { a, i, u, e, o } dan B = { 1, 2, 3, 4 }
a. Buatlah diagram panah yang menunjukkan
pemetaan f yang ditentukan oleh : a  1 ,
i  2 , u  1 , e  4 , o  2 .
b. Nyatakan pula dengan diagram cartesius
c . Nyatakan pula f sebagai himpunan
pasangan berurutan .

26. 8/22/2023 26
Jawab :
a . Diagram panah
. 1
. 2
. 3
. 4
a .
i .
u .
e .
o .
B
A

27. 8/22/2023 27
b. Diagram cartesius
1
a i u e o
0
2
3
4
5
6
7
8
9
10

28. 8/22/2023 28
{ (a , 1) , (i , 2) , (u , 1) , (e , 4) , (o , 2) }
c. Himpunan pasangan berurutan

29. 8/22/2023 29
3. Banyaknya pemetaan dari dua himpunan
Jika n(A) = a , dan n(B) = b , maka banyak
pemetaan yang mungkin terjadi dari
himpunan A ke B adalah ba dan
himpunan B ke A adalah ab
Contoh :
Berapa banyaknya pemetaan yang mungkin terjadi untuk pemetaan berikut :
a. Dari himpunan A = {a} dan B = {1}
b. Dari himpunan C = {1} dan D = { a , b }

30. 8/22/2023 30
c. Dari himpunan E = {a,b} dan F = {1}
d. Dari himpunan G = {1} dan H = { a,b,c }
e. Dari himpunan I = {1,2} dan J = { a,b}
f. Dari himpunan K = {a,i,u,e,o} dan L = {1,2,3}
g. Dari himpunan M = {a,b,c,d} dan N =
{1,2,3,4,5}
Jawab :
a. n(A) = 1 , n(B) = 1
Banyak pemetaan 11 = 1
b. n(C) = 1 , n(D) = 2
Banyak pemetaan 21 = 2

31. 8/22/2023 31
c. n(E) = 2 , n(F) = 1
Banyak pemetaan 12 = 1
d. n(G) = 1 , n(H) = 3
Banyak pemetaan 31 = 3
e. n(I) = 2 , n(J) = 2
Banyak pemetaan 22 = 4
f. n(K) = 5 , n(L) = 3
Banyak pemetaan 35 = 243
g. n(M) = 4 , n(N) = 5
Banyak pemetaan 54 = 625

32. 8/22/2023 32
f : x  y dibaca f memetakkan x ke y dan
dapat dinyatakan dengan f(x) .
Maka rumus fungsi dapat ditulis f(x) = y .
Contoh :
Diketahui suatu fungsi f : x  x + 2 dengan
daerah asal fungsi { x/ 1 < x < 6, x  A}
a. Tentukan rumus fungsi !
b. Tentukan daerah asal fungsi !
c . Tentukan daerah hasil fungsi !
d. Jika f(x) = 15 , maka tentukan nilai x !
4. Merumuskan suatu fungsi

33. 8/22/2023 33
a. Rumus fungsi f(x) = x +2
b. Daerah asal = { 2, 3, 4, 5 }
c. Daerah hasil : f(x) = x + 2
untuk x = 2  f(x) = 2 + 2 = 4
x = 3  f(x) = 3 + 2 = 5
x = 4  f(x) = 4 + 2 = 6
x = 5  f(x) = 5 + 2 = 7
Jadi daerah hasil fungsi : { 4, 5, 6, 7 }
d. f(x) = 15 x + 2 = 15
x = 15 – 2
x = 13 Jadi nilai x
= 13
Jawab :

34. 8/22/2023 34
5. Dengan tanpa membuat diagram
panahnya terlebih dahulu , tentukan
banyaknya pemetaan yang mungkin dari :
a. A = {a, b, c} B = {1, 2}
b. A = {1, 2} B = {a, b, c}
c. A = {a, b, c} B = {1, 2, 3}
d. A = {a, b, c} B = {1, 2, 3, 4}
e. A = {1, 2} B = {a, b, c, d}

35. 8/22/2023 35
C. Menghitung Nilai Fungsi
Untuk menghitung nilai fungsi dapat
digunakan rumus :
f (x) = ax + b
Contoh :
1. Suatu fungsi ditentukan dengan f : x  5x -
3
Tentukan :
a. Rumus funsi .
b. Nilai fungsi untuk x = 4 dan x = -1 .

36. 8/22/2023 36
Jawab :
a. Rumus fungsinya f(x) = 5x – 3
b. Nilai fungsi f(x) = 5x – 3
untuk x = 4 maka f(4) = 5 . 4 – 3 = 17
x = -1 maka f(-1) = 5 .(-1) – 3 = -8
Jadi nilai fungsi untuk x = 4 adalah 17
dan
x = -1 adalah -8

37. 8/22/2023 37
2.
Suatu fungsi dirumuskan g (x) = -4x +
Tentukan :
a. g ( -2 )
b. Nilai a jika g (a) = -5

38. 8/22/2023 38
Jawab :
a. g (x) = -4x + 3
g (- 2 ) = -4 . (- 2 ) + 3
= 8 + 3
= 11
b. g (a) = - 4a + 3
- 4a + 3 = - 5
- 4a = - 5 – 3
- 4a = - 8
a = 2

39. 8/22/2023 39
D. MENENTUKAN BENTUK
FUNGSI
Suatu fungsi dapat ditentukan bentuknya jika
data fungsi diketahui . Bentuk fungsi linier
dapat dirumuskan sebagai f (x) = ax + b .
Contoh :
Suatu fungsi ditentukan dengan rumus
f (x) = ax + b , jika f (2) = 10 dan f (-4) = -8 .
Tentukan :
a. Nilai a dan b
b. Bentuk fungsinya
c. Bayangan dari – 3

40. 8/22/2023 40
Jawab :
a. f (x) = ax + b
f (2) = 2a + b = 10  2a + b = 10
f (-4) = -4a + b = -8  -4a + b = -8 -
6a = 18
a = 3
untuk a = 3  2a + b = 10
2 . 3 + b = 10
6 + b = 10
b = 4
Jadi , nilai a = 3 dan b = 4

41. 8/22/2023 41
b. f (x) = ax + b
f (x) = 3x + 4
Jadi , bentuk fungsinya f (x) = 3x + 4
c. Bayangan dari – 3
f (x) = 3x + 4
f (- 3) = 3 ( - 3 ) + 4
= - 9 + 4
= - 5

42. 8/22/2023 42
E. Menggambar Grafik Fungsi
Untuk menggambar grafik fungsi ada
cara yang mudah yang dapat dilakukan
terlebih dahulu yaitu membuat tabel
dengan mendaftar semua daerah asalnya
.
1. Grafik Fungsi Linier
Contoh :
1. Gambarlah grafik fungsi f (x) = x +1
dengan domain {x/0 x 5 , x  C}



43. 8/22/2023 43
Jawab :
f (x) = x +1 daerah asal = { 0,1,2,3,4,5
}
{x,f(x)}
x+1
x
(2,3)
0 1 2 3 4 5
1 2 3 4 5 6
(0,1) (1,2) (3,4) (4,5) (5,6)

44. 8/22/2023 44
Grafiknya :
f (x) = x + 1 , x  c (0,1,2,3,4,5)
{(0,1),(1,2),(2,3),(3,4),(4,5),(5,6)}
1
1 2 3 4 5
0
2
3
4
5
6
7
8
9
10
x
+
1
x

45. 8/22/2023 45
2. a. Buatlah tabel fungsi g : x  -2x + 1
dengan
daerah asal { -4,-3,-2,-1,0,1,2,3 } !
b. Berdasarkan tabel tersebut tentukan :
(i) bayangan dari -2 , 0 , dan 2 !
(ii) himpunan pasangan berurutan !
(iii) gambarlah grafik fungsi tersebut
pada
bidang cartesius , kemudian
hubungkan titik-titik tersebut
sehingga

46. 8/22/2023 46
Jawab :
a. g (x) = - 2x + 1
1
x -4 -3 -2 -1 0 1 2 3
-2x
1
g (x)
8 6 4 2 0 -2 -4 -6
1
9 7 5 3 -1 -3 -5
1 1 1 1 1 1 1

47. 8/22/2023 47
b. (i) Bayangan dari :
-2 adalah 5
0 adalah 1
2 adalah -3
(ii) Himpunan pasangan berurutan :
{ (-4,9),(-3,7),(-2,5),(-1,3),(0,1),(1,-
1),
(2,-3),(3,-5) }

48. 8/22/2023 48
(iii) Grafiknya :
9
0
-1
-2
-3
-4
-1
-2
-3
-4
-5
1 2 3
1
2
3
4
5
6
7
8
g (x) = -2x + 1

49. 8/22/2023 49