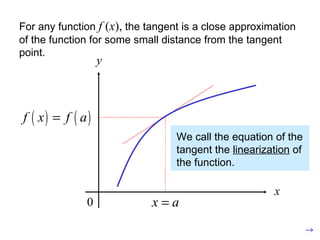
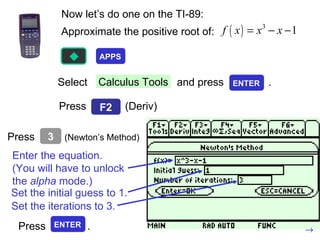
This document discusses linear approximations, differentials, and Newton's method for finding roots of functions. Linear approximations provide a linear equation that closely models a nonlinear function near a given point. Differentials represent very small changes in the variables of a function. Newton's method is an iterative algorithm that finds roots by taking successive guesses, using the slope of the tangent line at each guess to get closer to the root with each iteration. The document provides examples of applying these concepts to find how changes in variables impact a function and to approximate roots of equations.

1. 4.5: Linear Approximations, Differentials and Newton’s Method Greg Kelly, Hanford High School, Richland, Washington

2. For any function f ( x ), the tangent is a close approximation of the function for some small distance from the tangent point. We call the equation of the tangent the linearization of the function.

3. The linearization is the equation of the tangent line, and you can use the old formulas if you like. Start with the point/slope equation: linearization of f at a is the standard linear approximation of f at a.

4. Important linearizations for x near zero: This formula also leads to non-linear approximations:

5. Differentials: When we first started to talk about derivatives, we said that becomes when the change in x and change in y become very small. dy can be considered a very small change in y . dx can be considered a very small change in x .

6. Let be a differentiable function. The differential is an independent variable. The differential is:

7. Example: Consider a circle of radius 10. If the radius increases by 0.1, approximately how much will the area change? very small change in A very small change in r (approximate change in area)

8. (approximate change in area) Compare to actual change: New area: Old area:

9. Newton’s Method Finding a root for: We will use Newton’s Method to find the root between 2 and 3.

10. Guess: (not drawn to scale) (new guess)

11. Guess: (new guess)

12. Guess: (new guess)

13. Guess: Amazingly close to zero! This is Newton’s Method of finding roots. It is an example of an algorithm (a specific set of computational steps.) It is sometimes called the Newton-Raphson method This is a recursive algorithm because a set of steps are repeated with the previous answer put in the next repetition. Each repetition is called an iteration .

14. This is Newton’s Method of finding roots. It is an example of an algorithm (a specific set of computational steps.) It is sometimes called the Newton-Raphson method Guess: Amazingly close to zero! This is a recursive algorithm because a set of steps are repeated with the previous answer put in the next repetition. Each repetition is called an iteration . Newton’s Method:

15. Find where crosses .

16. There are some limitations to Newton’s method: Wrong root found Looking for this root. Bad guess. Failure to converge

17. Newton’s method is built in to the Calculus Tools application on the TI-89. Of course if you have a TI-89, you could just use the root finder to answer the problem. The only reason to use the calculator for Newton’s Method is to help your understanding or to check your work. It would not be allowed in a college course, on the AP exam or on one of my tests.

18. Now let’s do one on the TI-89: APPS Select and press . Calculus Tools ENTER If you see this screen, press , change the mode settings as necessary, and press again. ENTER APPS Approximate the positive root of:

19. Now let’s do one on the TI-89: Select and press . Calculus Tools Press (Deriv) Enter the equation. (You will have to unlock the alpha mode.) Set the initial guess to 1. Approximate the positive root of: Set the iterations to 3. APPS ENTER F2 Press (Newton’s Method) 3 Press . ENTER

20. Press to see the summary screen. ESC Press to see each iteration. ENTER

21.  Press and then to return your calculator to normal. ESC HOME