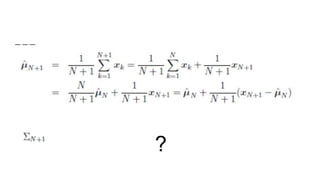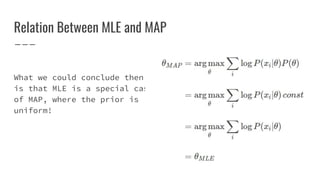
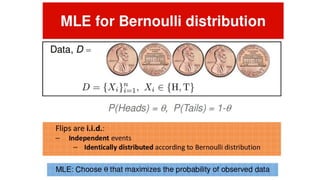
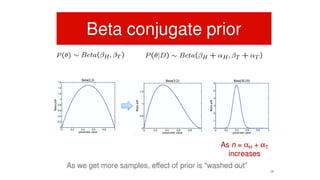
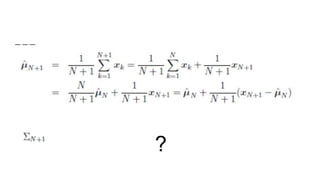
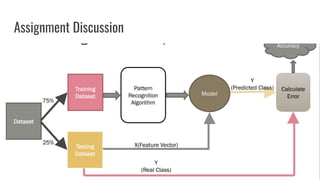
This document provides an overview of pattern recognition techniques including Bayesian decision classifiers, Bayes rule, and methods for estimating parameters like maximum likelihood estimation (MLE) and maximum a posteriori estimation (MAP). It discusses how MLE estimates parameters as fixed values by maximizing the likelihood function, while MAP includes a prior distribution and maximizes the posterior. MAP is a generalization of MLE, reducing to MLE when the prior is uniform. The document also lists problems and experiments but does not provide details.

1. Pattern Recognition
Tutorial 4- Aly Osama

2. Agenda
1. Short Review
2. Solving Sheets Problems
3. Experiments

3. Review

4. Design a Bayesian Decision Classifier?
Class-conditional densities Prior
We don’t have both in real life problems

5. Bayes Rule

6. How to estimate parameters ?
MLE vs MAP
1. Maximum Likelihood Estimation
a. Parameters are unknown but fixed
2. Maximum A Posteriori Estimation
a. Parameters are random variables having a priori distribution

7. 1. Maximum Likelihood Estimation
let’s say we have a likelihood function P(X|θ).
Then, the MLE for θ, the parameter we want to
infer, is:
To use this framework, we just need to derive the
log likelihood of our model, then maximizing it
with regard of θ using our favorite optimization
algorithm like Gradient Descent.

8. 2. Maximum a posterior Estimation
If we replace the likelihood in the MLE formula above with
the posterior, we get:
Comparing both MLE and MAP equation, the only
thing differs is the inclusion of prior P(θ) in MAP,
otherwise they are identical. What it means is that,
the likelihood is now weighted with some weight
coming from the prior.

9. Relation Between MLE and MAP
What we could conclude then,
is that MLE is a special case
of MAP, where the prior is
uniform!

18. Problems

19. Problem 1

20. Solution 1

21. Problem 2

23. Problem 3

25. ?

26. Problem 4

28. Experiments

29. Assignment Discussion

30. Assignment 4
Understand and compare your classifier using
● Accuracy
● Precision
● Recall
● F-Score