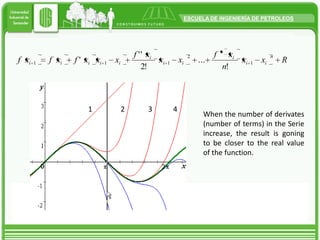
Taylor's approximation theorem allows functions to be approximated by polynomials in a specific point where the function is differentiable. It provides a finite series with a residual term to account for higher order terms. Taylor's series is useful for obtaining close approximations to the real solution of a function by using a finite number of terms. The more derivative terms that are included, the closer the result will be to the actual value of the function at that point.

1. RUBEN DARIO ARISMENDI RUEDA

2. CHAPTER 3: ‘TAYLOR’S APPROXIMATION’

3. Taylor's Series. Is a theorem that let us to obtain polynomics approximations of a function in an specific point where the function is diferenciable. As well, with this theorem we can delimit the range of error in the estimation.This is a finitiveserie, and the Residual term is include to considerate all the terms from (n+1) to infinitive.Taylor's SerieResidual term

4. McLaurin Serie.

5. HowisTaylor’s Serie Used and Whyisitimportant?Taylor’s serie isusedwith a finitivenumber of termsthatwillprovideusanapproximationreallyclosetothe real solution of thefunction.

6. 1234Whenthenumber of derivates (number of terms) in the Serie increase, theresultisgoningtobeclosertothe real value of thefunction.

7. NUMERICAL DIFFERENTIATION .FromtheTaylor’s serie of firstorder.WereflecttheFirstderivate: ; = hPROGRESSIVE DIFFERENTIATION

8. FromtheTaylor’s serie of firstorder.WereflecttheFirstderivate:; =hREGRESSIVE DIFFERENTIATION

9. FromtheTaylor’s serie of firstorder(Progressive and Regressive) -WereflecttheFirstderivate:CENTRATE DIFFERENTIATION

10. EXAMPLE.Determine theTaylor’sPolynom n = 4 , c = 1 = xiDEVELOPMENT.1.Find allthederivatesthatisneeded.

11. 2. Replacethevalues of thederivates in theTaylor’s Serie TofindthePolynom. At theend, Wewillhavethepolynomtogettheapproximatevalue of thefunction