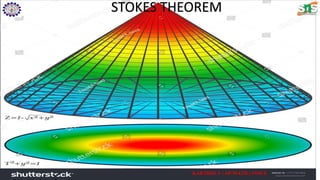
Stokes' theorem connects surface integrals of a vector field's curl to line integrals around the boundary, making it essential in vector calculus for analyzing flux in three-dimensional space. The document outlines the definitions and applications of vector calculus concepts like line and surface integrals, closed surfaces, and the conditions necessary for applying Stokes' theorem in contexts such as physics and engineering. Visual representations and calculation examples demonstrate the practical implications of Stokes' theorem in various fields.

1. STOKES THEOREM
KARTHIK.V | AP/MATH | SNSCE

2. Introduction to Stokes'
Theorem
Stokes' Theorem is a fundamental theorem in vector calculus that relates
a surface integral of a vector field to a line integral of the field's curl. It
provides a powerful tool for evaluating flux across a surface in three-
dimensional space.
KARTHIK.V | AP/MATH | SNSCE

3. Overview of Vector Calculus
Scalar and Vector
Fields
Vector calculus deals
with the study of scalar
and vector fields in
three-dimensional
space.
Gradient,
Divergence, Curl
Topics include
gradients, divergence,
curl, and their
applications in physics
and engineering.
Line and Surface
Integrals
Line and surface
integrals play a key
role in defining and
understanding vector
calculus concepts.
KARTHIK.V | AP/MATH | SNSCE

4. Understanding Line Integrals
• Definition: Line integrals measure the total effect of a vector field along a curve.
• Direction: Positive and negative results indicate the direction of the flow along the curve.
• Applications: Widely used in physics, engineering, and computer graphics for various calculations.
KARTHIK.V | AP/MATH | SNSCE

5. Explanation of Surface Integrals
1 Definition
A surface integral involves the integration of a scalar or vector field over a
surface. It measures the flux of the field through the surface.
2 Surface Orientation
The orientation of the surface plays a crucial role in determining the direction
of the flux and is essential for correctly setting up the integral.
3 Applications
Surface integrals are used in physics, engineering, and fluid dynamics to
calculate quantities like flow rates, electric flux, and surface area.
KARTHIK.V | AP/MATH | SNSCE

6. The Concept of a Closed Surface
Definition
A closed surface is a
surface that completely
encloses a finite volume
within itself. It has no
boundaries or openings,
and it is often used in
vector calculus to
understand concepts of
flux and circulation.
Application
In physics, closed
surfaces are essential for
understanding the flow of
vector fields such as
electric and magnetic
fields. They allow for the
calculation of flux, which
measures the flow of a
vector field through the
surface.
Mathematical
Representation
A closed surface can be
mathematically
represented using
equations that describe
its boundaries and any
internal volumes. These
representations are
crucial for the application
of Stokes' Theorem and
other vector calculus
concepts.
KARTHIK.V | AP/MATH | SNSCE

7. Stokes' Theorem
In vector calculus, Stokes' Theorem relates a surface integral of the curl
of a vector field to a line integral of the vector field around the boundary of
the surface. It provides a fundamental connection between line integrals
and surface integrals.
KARTHIK.V | AP/MATH | SNSCE

8. Visual representation of Stokes'
Theorem
Vector Field
Visualization
An illustration depicting a
vector field over a closed
surface, showcasing the
flow and divergence of the
field.
Circulation and
Integration
A graphic demonstrating
the concept of circulation
and its relationship to line
integrals over a closed
curve.
Flux and Surface
Integrals
An image displaying the
flux of a vector field
through a surface,
highlighting the connection
to surface integrals.
KARTHIK.V | AP/MATH | SNSCE

9. Application of Stokes' Theorem in
Physics
Stokes' Theorem finds widespread application in physics, particularly in the fields of fluid
dynamics, electromagnetism, and quantum mechanics. It allows for the conversion of
complex surface integrals into simpler line integrals, providing a powerful tool for analyzing
vector fields in three-dimensional space.
KARTHIK.V | AP/MATH | SNSCE

10. Examples of calculating line integrals
using Stokes' Theorem
Identify the vector field
Begin by identifying the vector field involved in the line integral.
Choose a closed curve
Select a closed curve that encompasses the surface of interest.
Apply Stokes' Theorem
Use the theorem to find the line integral by evaluating the curl of the vector
field over the surface.
KARTHIK.V | AP/MATH | SNSCE

11. Examples of calculating surface
integrals using Stokes' Theorem
Surface Shape Vector Field Resultant Surface Integral
Planar Surface Divergence-Free Vector Field Calculate Flux
Spherical Surface Curl-Free Vector Field Calculate Circulation
Toroidal Surface Irrotational Vector Field Compute Stream Function
KARTHIK.V | AP/MATH | SNSCE

12. KARTHIK.V | AP/MATH | SNSCE