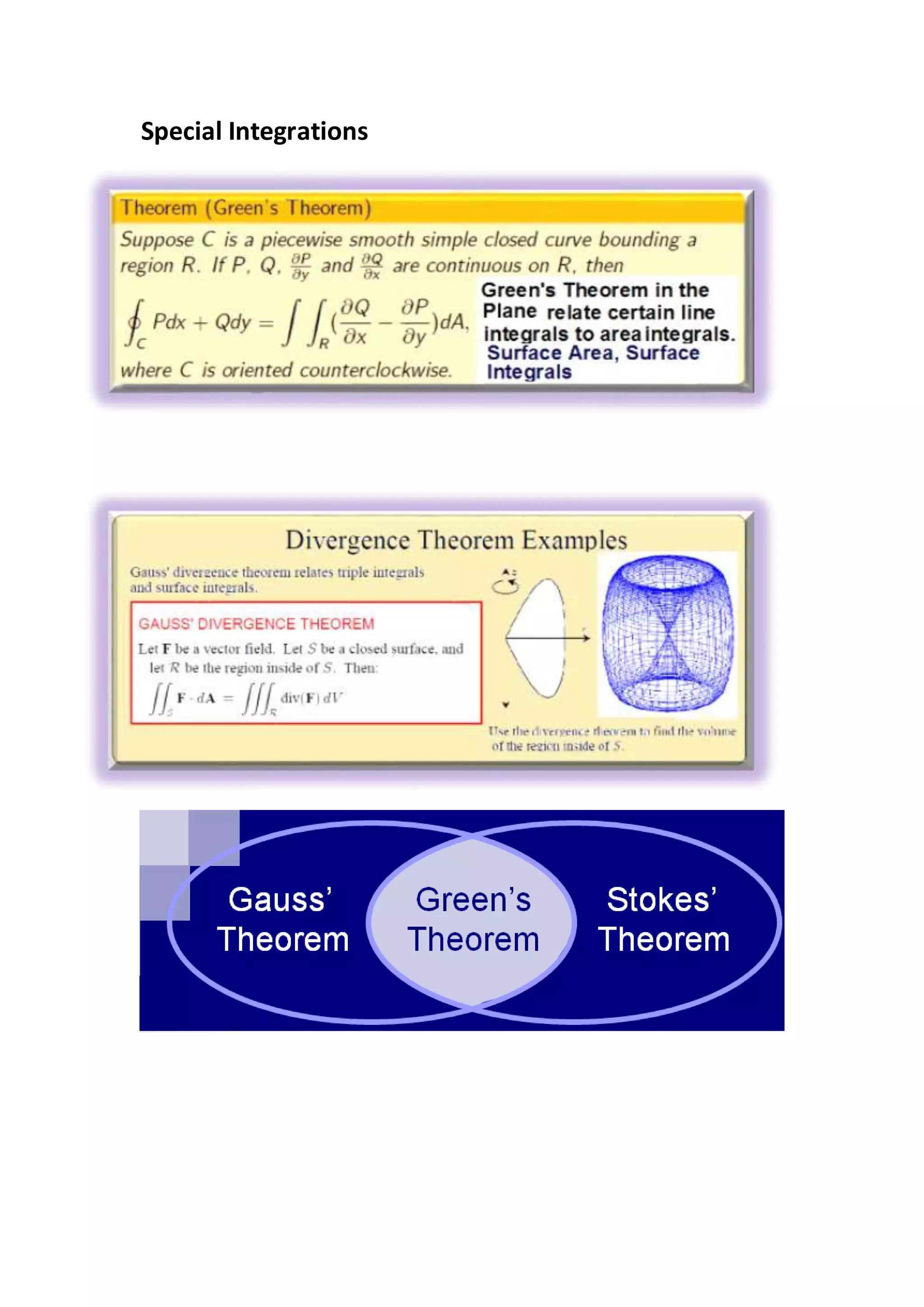
This document discusses Green's Theorem and related mathematical concepts. It provides biographical information about George Green and describes his contributions to developing Green's Theorem. Green's Theorem allows transforming a line integral into a surface integral, and was an important step in James Maxwell developing his equations of electromagnetism. Stokes' Theorem, discovered by Lord Kelvin, provides a similar transformation between line and surface integrals in three-dimensional space. Applications of these theorems include fluid dynamics, gravity, and quantum physics.

1. Special Integrations

2. Green’s Theorem
George Green
July 14, 1793 - May 31, 1841
British mathematicianand physicist
First person to try to explain a mathematicaltheory
of electricity and magnetism
!taught-selfAlmost entirely
Published “An Essay on the Application of
Mathematical Analysis to the Theories of Electricity
and Magnetism” in 1828.
Entered Cambridge University as an undergraduate
in 1833 at age 40.
The Theory
Consider a simple closed curve C, and let D be
the region enclosed by the curve.

3. :Notes
•in theno holesThe simple, closed curve has
region D
•A direction has been put on the curve with the
convention that the curve C
leftis on theDif the regionpositive orientationhas a
as we traverse the path.
Example
A particle moves once counterclockwise about the circle
of radius 6 about the origin, under the influence of the
force.
dA
y
f
x
g
gdyfdx
C D
  











jxyixxyeF x ˆ)(ˆ))cosh(( 2/3



4. Calculatethe work done.
 )sin(6),cos(6)( tttC 
)2,0(: tI

5. Green’s Theorem…andbeyond
Green’s Theorem is a crucial component in the
developmentof many famous works:
James Maxwell’sEquations
Gauss’ Divergence Theorem
Stokes’ Integral Theorem

6. Gauss’ Divergence Theorem
Gauss in the House
German mathematician,lived 1777-1855
Born in Braunschweig, Duchy of Braunschweig-
Lüneburg in Northwestern Germany
DisquisitionesPublishedArithmeticaewhen hewas
21(and what haveyoudone today)?
As a workaholic,was once interrupted while
working and told his wife was dying. He replied
“tell her to wait a moment until I’m finished”.
Gauss’ Divergence Theorem
The integral of a continuously differentiable
vector field across a boundary (flux) is equal
to the integral of the divergence of that vector
field within the region enclosed by the
boundary.

7. Applications
The Aerodynamic Continuity Equation
The surface integral of mass flux around a
control volume without sources or sinks is
equal to the rate of mass storage.
If the flow at a particular point is
incompressible, then the net velocity flux
around the control volume must be zero.
As net velocity flux at a point requires
taking the limit of an integral, one instead
merely calculates the divergence.
If the divergence at that point is zero,
then it is incompressible. If it is positive,
the fluid is expanding, and vice versa
Gauss’s Theorem can be applied to any vector
field which obeys an inverse-square law
(except at the origin), such as gravity,
electrostatic attraction, and even examples in
quantum physics such as probability density.

8. Example
Assumethere is a unit circle centered on the
)2
,xz2
origin and a vector field V(x,y,z)=(xyz,y
To find the vector flux of the field across the
surface of the sphere, both the unit normal
integral and the Gauss’ divergence integral
will be computed

9. The Integral Theoremof Stokes

10. •Irish mathematicianand physicist who
attended Pembroke College (Cambridge
University).
•Stokes was the oldest of the trio of natural
philosophers who contributed to the fame of
the Cambridge University school of
th
Mathematical Physics in the middle of the 19
century. The others were:
•James Clark Maxwell - Maxwell’s Equations,
electricity, magnetism and inductance.
•Lord Kelvin - Thermodynamics, absolute
temperature scale.
•Stokes’Theorem
•Interesting Fact : This theorem is also known
as the Kelvin – Stokes Theorem because it was
actually discovered by Lord Kelvin. Kelvin
then presented his discovery in a letter to
Stokes. Stokes, who was teaching at
Cambridge at the time, made the theory a
proof on the Smith’s Prize exam and the name

11. stuck. Additionally, this theorem was used in
the derivation of 2 of Maxwell’s Equations!
•Given: A three dimensional surface Σ in a
vector field F. It’s boundary is denoted by ∂∑
orientation n.
So what does it mean?
Simply said, the surface integral of the curl of a
vector field over a three dimensional surface is
equal to the line integral of the vector field over
the boundary of the surface.

12. As Greene’s Theorem provides the transformation
from a line integral to a surface integral, Stokes’
theorem provides the transformation from a line
integral to a surface integral in three-dimensional
space.