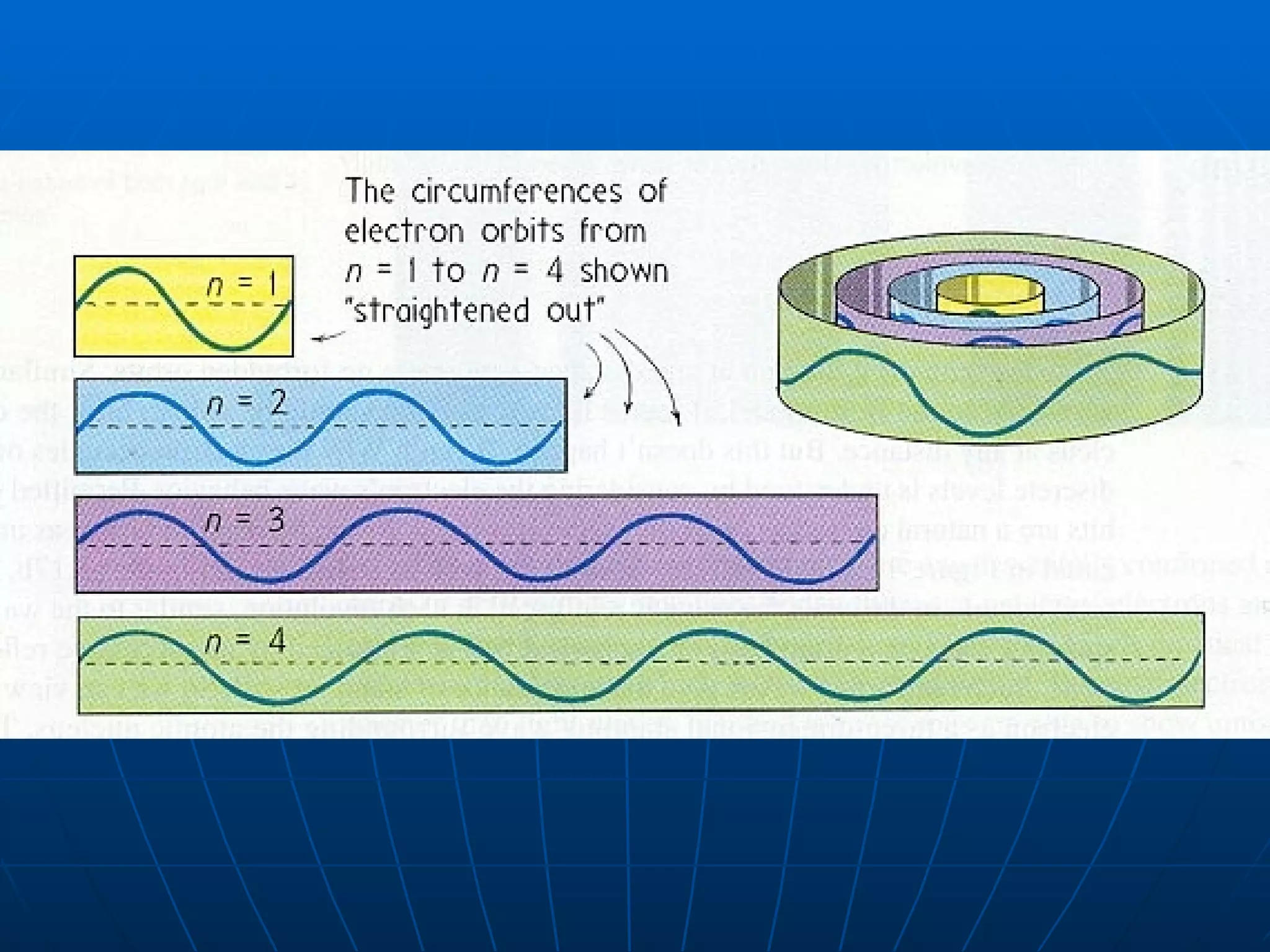
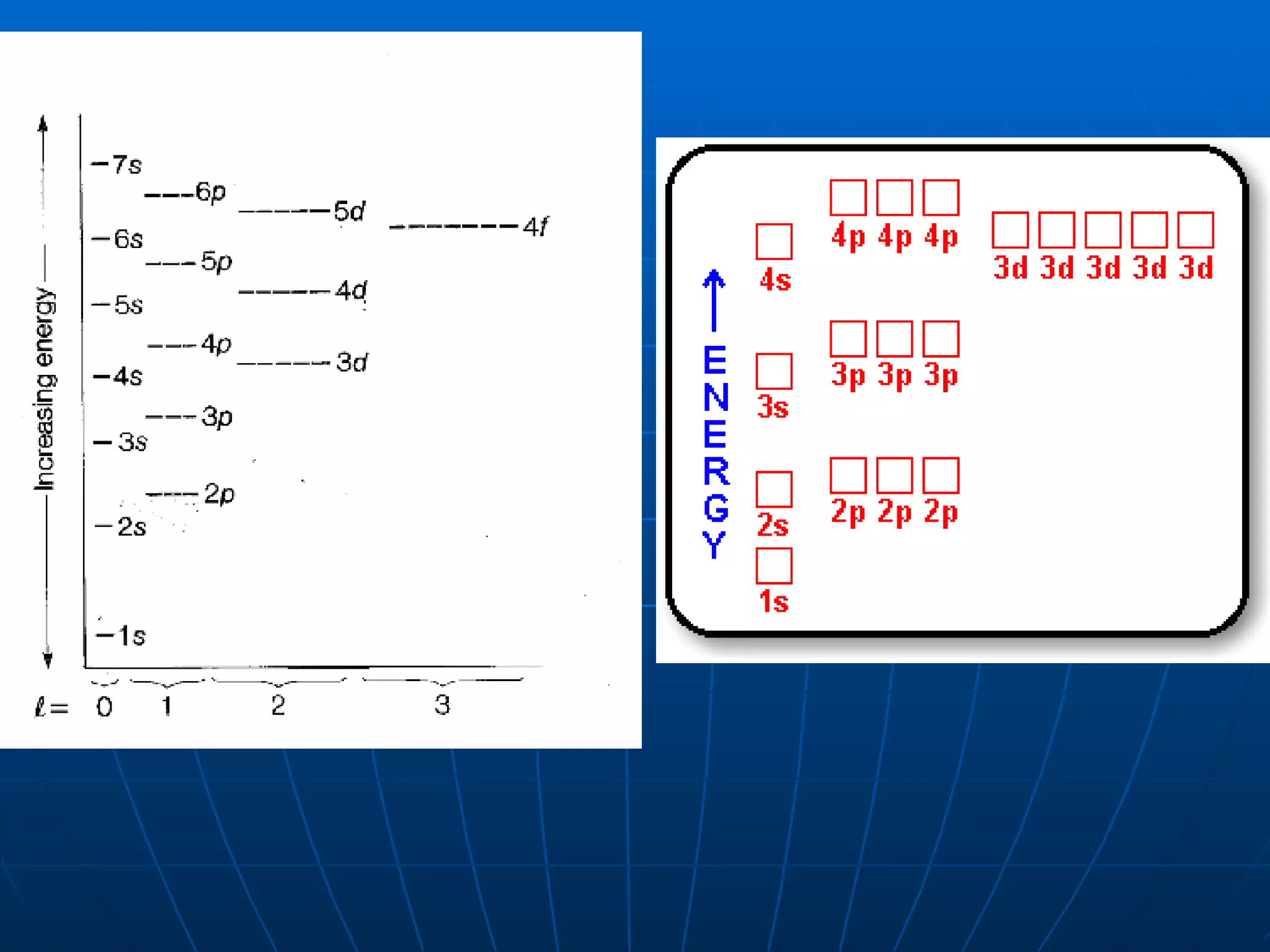
1. The quantum mechanical model of the atom describes electrons as existing in orbitals defined by four quantum numbers rather than following circular orbits. 2. The quantum numbers specify the principal energy level, subshell type, orientation in space, and spin of each electron. 3. Electrons fill atomic orbitals according to increasing energy levels, with each level and sublevel having a fixed capacity for electrons.

1. Light, Energy, and More October 23, 2007 Chemistry

2. Recap… Electromagnetic Spectrum High Energy Low Energy Wave Nature of Light

4. What’s Going On Here?

5. When we heat metal what happens?

6. Does the wave model of light explain these changes? Does not explain different wavelengths and frequencies at different temperatures What is light? Radiation….what is radiation? Particles or rays of energy What is temperature anyways? The measure of the average kinetic energy of the particles in an object Kinetic Energy vs. Potential Energy Too many questions….

7. Max Planck (1900) German Physicist Began to look for answers Matter can only gain or lose energy in small quantized amounts What’s quantized?

8. Vocab Word!!! QUANTUM Minimum amount of energy that can be gained or lost by an atom The emitted light from a glowing metal is a ENERGY…this energy is quantized

9. If energy is now quantized…how can we determine the amount of energy of a quantum? What is energy measured in? What are we observing? What happens to the color when we increase the temperature (energy)? Proportional or inversely proportional? Now we need a constant… Planck’s constant, h=6.626 x 10^-34 J*s

11. Time to put these words into action! What is the frequency and wavelength electromagnetic radiation that emits 1.68 x 10^-17 J of energy? What type of electromagnetic radiation is this? Wavelength= 1.18 x 10^-8 m Ultraviolet radiation

12. Some questions to answer… What is the color we see? What happens to the energy of the radiation when we increase the frequency, v, of the radiation emitted? Iron at room temp…color and E? Iron with a little heat…color and E? Iron with lots of heat…color and E?

13. According to Planck’s Theory… If we have a given v, matter can emit or absorb E only in whole number multiples of hv (1hv, 2hv, 3 hv…) Matter can ONLY have specific amounts of energy Wall of kids building blocks We can only add or take away in increments of whole blocks…we cannot remove half a block

14. The Big Mystery of the 1900’s… The Photoelectric Effect… What caused these color changes in metals???

15. Photoelectric Effect Electrons (photoelectrons) are emitted from a metal’s surface when a light of a certain frequency shines on the surface Certain specific amounts of energy (what’s this called???) needed to knock out electrons from metal atoms.

17. Albert Einstein (1905) Added onto Planck’s Theory… Called the electron’s emitted, PHOTONS (the little energy packets Planck called quantums) Now… E photon = hv

18. Planck paved the way for the explanation behind the mystery But some one else came into the picture…

19. Now light is not just a wave… Einstein’s Dual Nature of Light Particle and wave characteristics Light is a beam of tiny particles, called photons, acting like a wave

20. NEW WORD!!! Photon A particle of electromagnetic radiation with no mass that carries a quantum of energy

22. What Einstein added… Energy of a photon has a minimum or threshold value to eject photoelectrons What must happen for the photoelectric effect to occur? Energy of a photon (particle of EM radiation) must have the minimum energy requirement to free the electron from the atom of metal

23. Mystery Solved! No matter how long a light of a certain frequency is shone on metal (intensity), electrons will not be ejected unless the minimum amount of energy is shone. Silver metal Photoelectrons ejected when a light with a frequency of at least 1.14 x 10^15 Hz or greater is used Sodium metal Red light Violet light

24. Revised Planck’s Work… Einstein piggy-backed off of Planck’s Theory and we now have….. Photon

25. Time to do a little work…. Tiny water drops in the air disperse the white light of the sun into a rainbow. What is the Energy oa a photon from the violet portion of the rainbow if it has a frequency of 7.23x10^14 Hz? E=4.79 x 10^-19 J Energy in a photon of violet light

26. A couple more…  A photon has an energy of 2.93 x 10^-25 J. What is its frequency? What type of electromagnetic radiation is the photon? V=4.42 x 10^8 Hz TV or FM waves

27. Practice makes perfect…  What is the energy of each photon in the following types of radiation? 6.32 x 10^20 Hz 9.50 x 10^13 Hz 1.05 x 10^16 Hz What types of radiation are each? 4.19 x 10^-13 J gamma or x-ray 6.29 x 10^20 J infrared 6.96 x 10^-18 J ultraviolet

28. How does this work? (Neon Signs)

29. What do we know about neon signs? Electricity is passed through tube full of neon gas Neon atoms in tube absorb this energy What happens when something absorbs energy? Neon atoms in tube become excited Stable of Unstable? What happens when something is unstable? What do we see released energy as? Electromagnetic radiation…visible light!!!

30. EM spectrum What happens when we pass sunlight through a prism? Continuous spectrum of colors ROYGBIV

31. What happens when we pass light from neon gas or hydrogen gas through prism? Separation of colors Discontinuous spectrum This is called…

32. ATOMIC EMISSION SPECTRUM (AES) AES of an element is the set of frequencies of the electromagnetic radiation emitted by the atoms of that element Individual lines of color Only certain lines of color appear for certain elements… What does this mean…???? Every element has a unique AES Why is this important?

35. Hydrogen Atom Why did scientists want to use hydrogen? How many protons? How many electrons? Do you think it is easy to use? Check out the AES of hydrogen gas…

37. Neils Bohr (1913) Danish Physicist Worked with Rutherford Quantum Model of Hydrogen atom Predicted lines of Hydrogen AES

38. Hydrogen has only one electron but why do we get different colored lines on AES??? We get hydrogen atoms excited… Electrons move to excited levels H has certain allowable energy states…. The lowest energy state is called the GROUND STATE

39. Bohr’s Hydrogen Orbits… He related H’s energy states to the motion of an electron in an atom Single electron in moves around nucleus in circular orbits Smaller orbit, smaller radius, closer to nucleus means…? Lower energy level Larger orbit, larger radius, farther from the nucleus means…? Higher energy level

41. Bohr’s Quantum Model Assigned quantum numbers, n, to each orbit Calculated orbits radius Chart on page 127 1 st orbit  n=1 (first energy level) 2 nd orbit  n=2 (second energy level) 3 rd orbit  n=3 (third energy level)

44. When we add energy, what happens to electron? Electron excited Moves to next energy level Excited=? unstable What happens when something is unstable? Wants to get back to being stable Releases energy Goes back down to lower energy level Photon is emitted corresponding to the 2 different energy levels associated with the 2 orbits

46. NEW EQUATION /_\ E= E higher e- orbit - E lower e- orbit =E photon =hv Only certain energies are possible so only certain frequencies, v, of EM radiation are emitted Lets look at the AES of Hydrogen…

47. How many lines are there? So how many different types of radiations are we seeing? There are 4 electron transitions account for lines in the hydrogen spectrum Going from 3 rd orbital to 2 nd orbital… Going from 4 th orbital to 2 nd orbital… Going from 5 th orbital to 2 nd orbital… Going from 6 th orbital to 2 nd orbital…

48. Names for these lines… Balmer Series The 4 visible color lines Electrons that drop into n=2 Other electrons transitions not visible Lyman series Ultraviolet light Electrons drop into n=1 Paschen series Infrared Electrons drop into n=3

50. Problems with Bohr’s Model Predicted AES lines of H but not any other elements Did not account for all chemical behavior Big problem… Electrons don’t move in circular orbits Time for a new model…

52. Louis De Broglie (1924) French physics graduate student Proposed idea that accounted for the fixed energy levels in Bohr’s model

53. If waves can have particle like characteristics, then can particles, such as electrons, have wave like characteristics???

54. What he knew… Electrons have wavelike motion (because it’s a particle) An electron had restricted orbits Each orbit had a fixed radius from the nucleus Are a wide variety of wavelengths, frequencies, and energies possible?

56. No…there could only be allowed certain possible frequencies, wavelengths, and energies in an atom De Broglie came up with an equation for the wavelength of a particle of mass (m) moving at velocity (v).

57. De Broglie’s Equation

58. What does this equation do? What are we using? Wavelength Planck’s constant Mass of the particle Velocity Tells us that all moving particles have wave-like characteristics

59. Food for thought… Cars? Baseball? Do these have wavelike characteristics? Why or why not?

60. Yes…let’s look at the equation… λ = h mv The car and the baseball do have a velocity and a mass… Using De Broglie’s equation we do get a wavelength for the movement of a baseball and a car… Let’s try the calculation…

61. Problem time… Mass of car= 910 kg Velocity of car= 25m/s What is the wavelength of the moving car? 2.9 x 10^-38 m How big is this? Can we see or measure this wavelength? No, much to small to be detected, even with the most sophisticated equipment

62. Another one… Electron speed= 25 m/s Electron mass= 9.11 x 10^-28 g What is the wavelength of the moving electron? 2.9 x 10^-5 m Do you think we can measure this wavelength and see it? Yes, with the right equipment

63. Practice makes perfect  What is the wavelength of an electron of mass 9.11 x 10-28 kg traveling at a velocity of 2.00 x 108 m/s? (Planck's constant = 6.63 x 10-34 J/Hz. 3.64 x 10-15m.

65. Werner Heisenberg (1901-1976) German theoretical physicist Drew conclusion from Rutherford, Bohr, and De Broglie’s models

66. Problem with finding the position of an electron Helium balloon in a dark room How would you determine the location of this balloon? Is the balloon going to stay in the same position? Energy transfer What if I gave you a flashlight? What happens when we shine a beam of light on the balloon?

67. Photons from light that reflect off of the balloon reach our eyes and tell us where the balloon is Is there a transfer of energy? How big is the balloon compared to the photons? Can we do the same thing with finding the location of an electron in an atom? Heisenberg focused on the interactions between photons and electrons…

68. Heisenberg Uncertainty Principle It is fundamentally impossible to know precisely both the velocity and position of a particle at the same time

69. Erwin Schrodinger (1926) Austrian physicist Furthered De Broglie’s wave-particle theory Derived equation that treated hydrogen’s electron as a wave Unlike Bohr’s, his fit well with atoms of different elements

70. Quantum Mechanical Model of the atom

71. The Quantum Mechanical Model Similar to Bohr’s… Limits an electron’s energy to certain values Unlike Bohr’s… What did Bohr say about the orbit of an electron around the nucleus? The Quantum Mechanic Model makes no attempt to describe the electron’s path

72. Schrodinger’s wave equation Solutions to equation called wave function Don’t worry about the equation its self…just know the basics…. Wave function  probability of finding the electron within a particular volume of space around the nucleus High probability  more likely to occur Low probability  less likely to occur

73. What the wave function tells us The atomic orbital of the electron Atomic orbital  3-D region around nucleus Fuzzy Cloud Density of the cloud at a given point is proportional to the probability of finding the electron at that point

74. New Word Orbital  region of space where there is a 90% probability of finding an electron of a given energy “electron cloud” Orbital

75. What did Bohr assign to electron orbitals? Quantum numbers Quantum Mechanical Model does the same…

76. Four Quantum Numbers: Specify the “address” (zip code) of each electron in an atom

77. First number…Principal Quantum Number ( n) Energy level (associated with the electron) Size if orbital Lowest energy level is assigned principle quantum number of 1 (n=1) Ground state What do you think happens as we increase n? Orbital becomes larger Electron spends more time farther away from the nucleus  atom’s energy increases

78. Principle energy levels contain… Energy Sublevels

79. Principle energy level 1  single sublevel Principle energy level 2  two sublevels Principle energy level 3  three sublevels What pattern do you see in the number of sublevels as we move further away from the nucleus? They increase as n increases (the further we get from the nucleus) UPPER LEVEL

80. Electron’s are labeled according to n value In atom’s with more than one electron, two or more electron’s may have the same n value They are in the same “electron shell”

81. Second quantum number Angular Momentum Quantum Number (l)

82. Each value of l corresponds to a different type of orbital with a different shape Value of n controls l (subshells possible) Angular momentum numbers can equal 0, 1, 2, 3… l=n-1 When n=1, l=0  only one possible subshell When n=2, l=0,1  two possible subshells

83. What the number of l means… Corresponds to the name of the subshell L=0  subshell s L=1  subshell p L=2  subshell d L=3  subshell f

84. S P D F: THE SUBLEVELS Each of these 4 sublevels has a unique shape Each orbital may contain at most, 2 electrons LETTERS ORIGINATED FROM DESCRIPTIONS OF THEIR SPECTRAL LINES S  sharp…spherical P  principal…dumbbell shaped D  diffuse…not all the same shape F  fundamental…not all the same shape

87. When principle energy level n=1, then l=0, which means there is only a single sublevel (one orbital) which is the small, spherical 1s When principle energy level n=2, then l can equal 0 or 1, which means that there are two sublevels (orbitals) 2s and 2p 2s sublevel  bigger than 1s, still sphere 2p sublevel  three dumbbell shaped p orbitals of equal energy called 2px, 2py, and 2pz The letters are just there to tell you what axis the electrons go on: x,y, or z axis When the principle energy level n=3, then l can equal 0,1, or 2, which means that there are 3 possible sublevels: 3s, sphere, bigger than 1s and 2s 3p, dumbbells 3d Each d sublevel consists 5 orbitals of equal energy Four d orbitals have same shape but different orientations Fifth d orbital, 3d z2 is shaped and oriented different from the other four When the principle energy level n=4, then 1 can equal 0,1,2, or 3 which means l=n-1=4 possible sublevels: Seven f orbitals of equal energy ( 2 electrons in each orbital) 4s, sphere 4p, dumbbells 4d, 4f

88. n = # of sublevels per level n 2 = # of orbitals per level Sublevel sets: 1 s, 3 p, 5 d, 7 f

91. Orbitals combine to form a spherical shape. 2s 2p z 2p y 2p x

92. Remember… 1. Principal #  energy level 2. Ang. Mom. #  sublevel (s,p,d,f) There are two more quantum numbers (3 and 4) we will discuss next class

93. Third Quantum Number M l  specifies the orientation of the orbital in space containing the electron Tells us whether the orbital is on the x, y, or z axis

94. Fourth Quantum Number M s  related to the direction of the electron spin Tells us if electron has a clockwise spin or counter clockwise spin Specifies orientation of electrons spin axis

95. Recap… Bohr? Orbits explained hydrogen’s quantized energy states De Broglie? Dual particle and wave nature of electrons Schrodinger? Wave equation predicted existence of atomic orbitals containing electrons

96. Electron Configuration Definition: arrangement of electrons in an atom Basic rules for filling up orbital's with electrons Which is more stable, low energy or high energy? So which orbitals are going to be filled up first? We are going to want an arrangement that gives us the lowest possible energy

97. Ground state electron configuration The most stable, lowest energy electron arrangement of an atom Each element has a ground-state electron configuration

98. Three Rules for Electron Arrangement Aufbau Principle Pauli Exclusion Principle Hund’s Rule

99. Aufbau Principle Each electron occupies the lowest energy orbital available In order to do this, you must learn the sequence of atomic orbitals from lowest to highest energy Aufbau Diagram Each box represents an orbital Each arrow represents an electron Only two arrows per box… Only two electrons per orbital

102. Some important things to remember about Aufbau… All orbitals related to an energy sublevel are of equal energy All three 2p orbitals have the same energy In a multi-electron atom, the energy sublevels within a principle energy level have different energies All three 2p orbitals are of higher energy than the one 2s orbital

104. In order of increasing energies, the sequence of energy sublevels within a principle energy level is s, p, d, f Orbitals related to energy sublevels within one principle energy level can overlap orbitals related to energy sublevels within another principle level Ex. An orbital related to the atoms 4s sublevel has a lower energy than the five orbitals related to 3d sublevel.

106. Pauli Exclusion Principle States that a maximum on 2 electrons can occupy a single atomic orbital but only if the electrons have opposite spins Wolfgang Pauli Austrian Physicist Observed atoms in excited states

107. Each electron has a spin Kinda like a spinning top It can only spin in one of 2 directions In order for electrons to be together in an orbital, they must have opposite spins

108. Hund’s Rule What kind of charge do electrons have? Do they attract or repel each other? So…….. Hund’s Rule states that single electrons with the same spin must occupy all each energy equal orbital before additional electrons with opposite spins can occupy the same orbital

109. 2p orbitals

110. Read section 5-3!