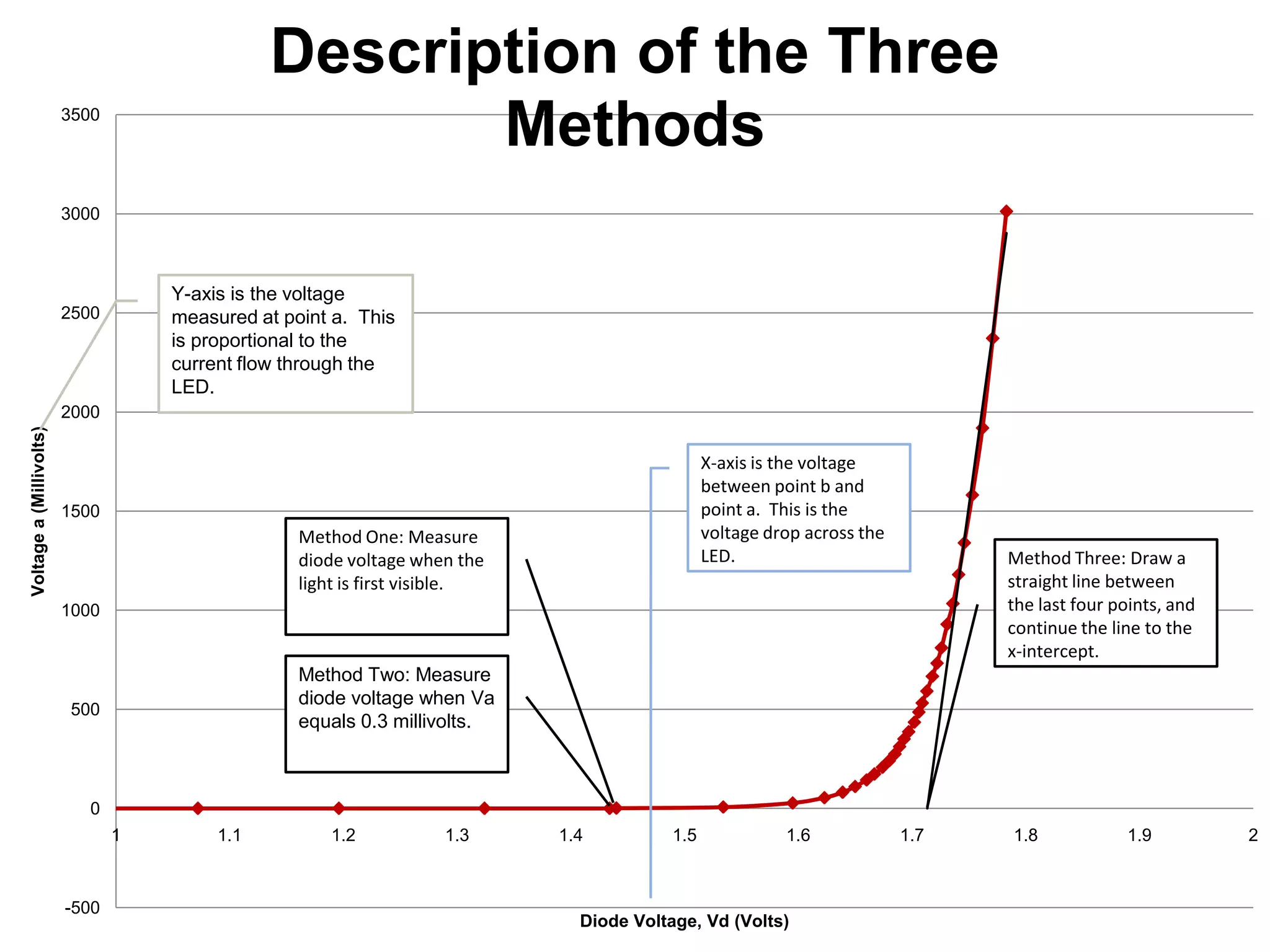
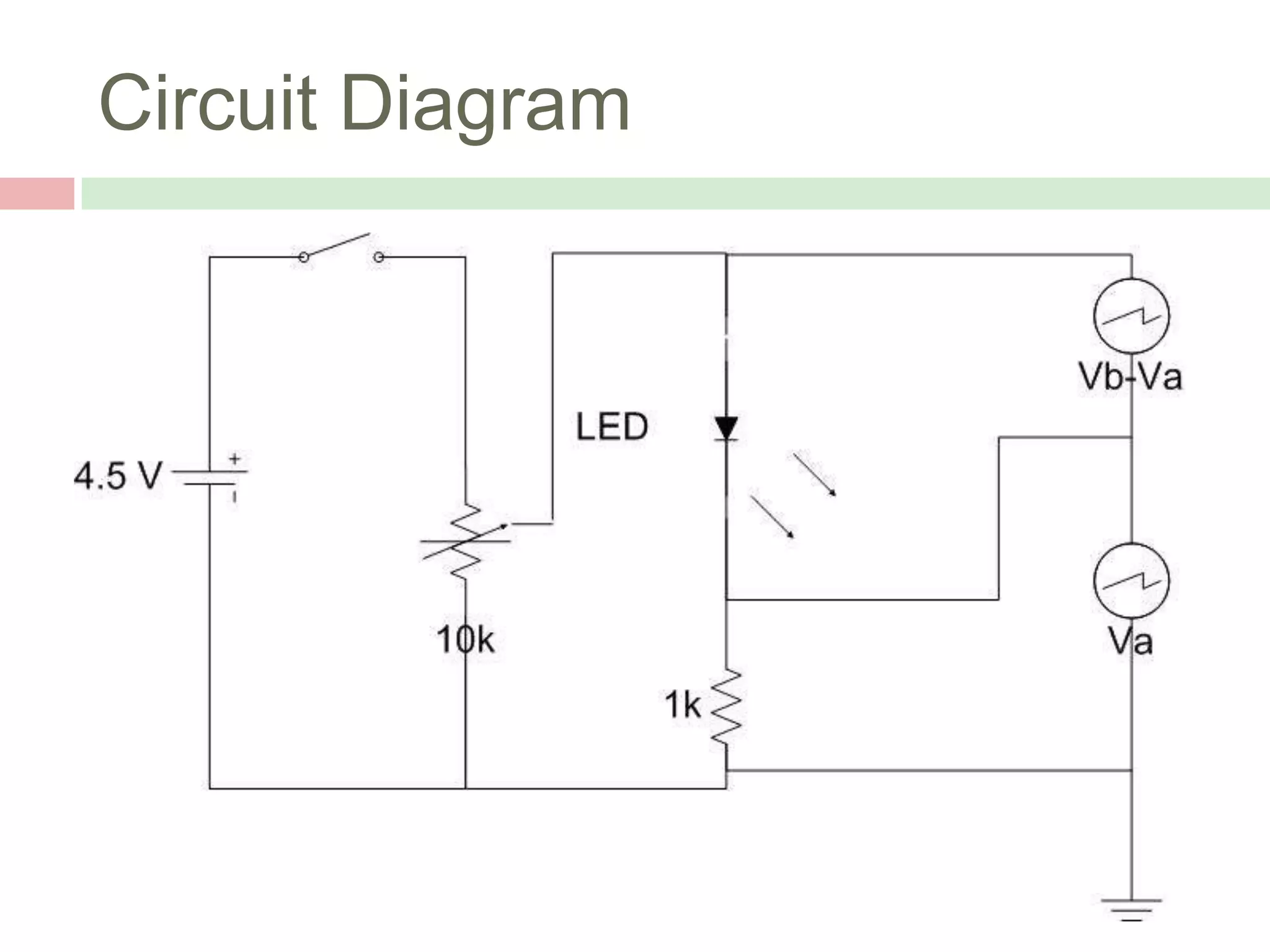
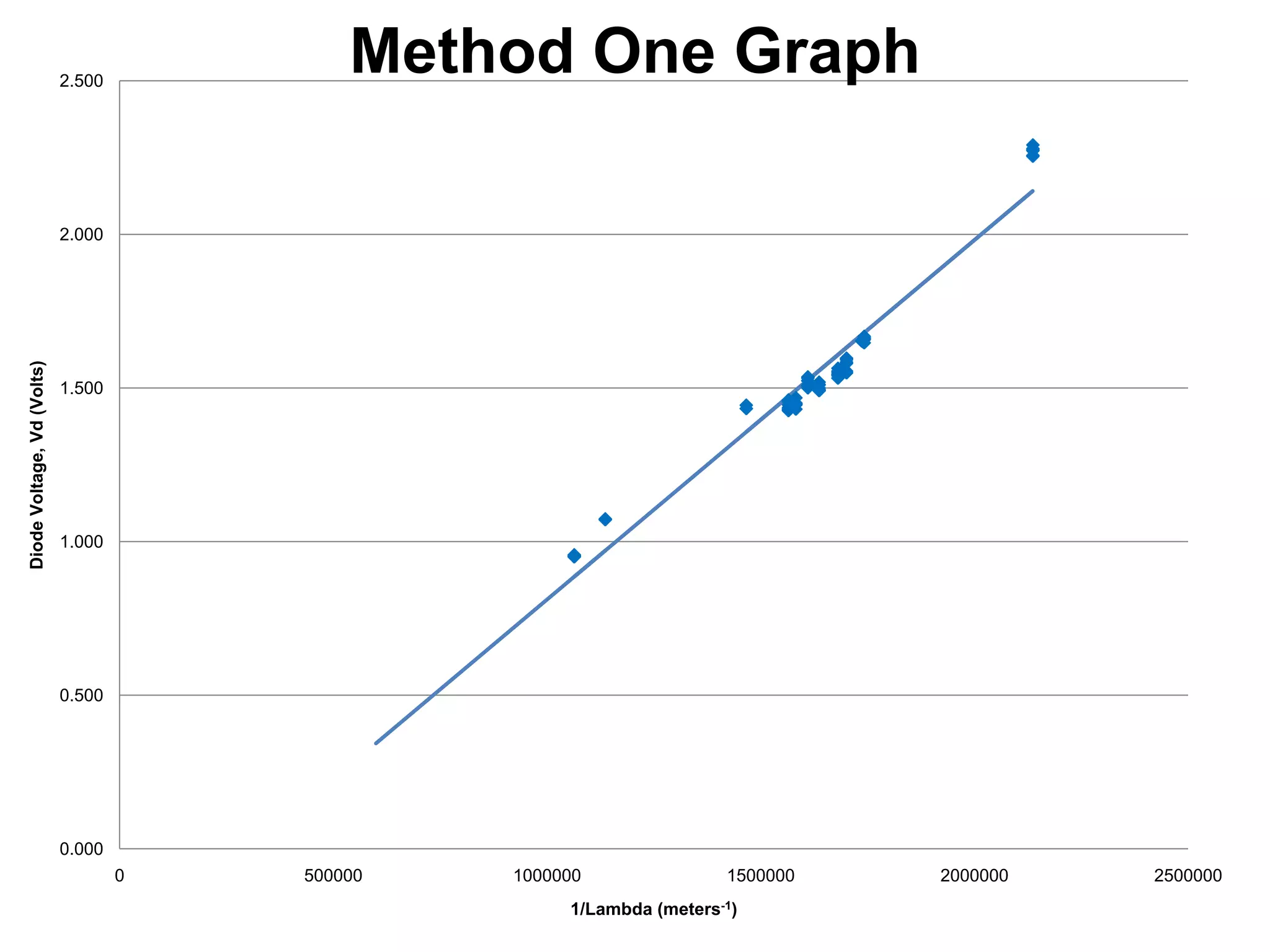
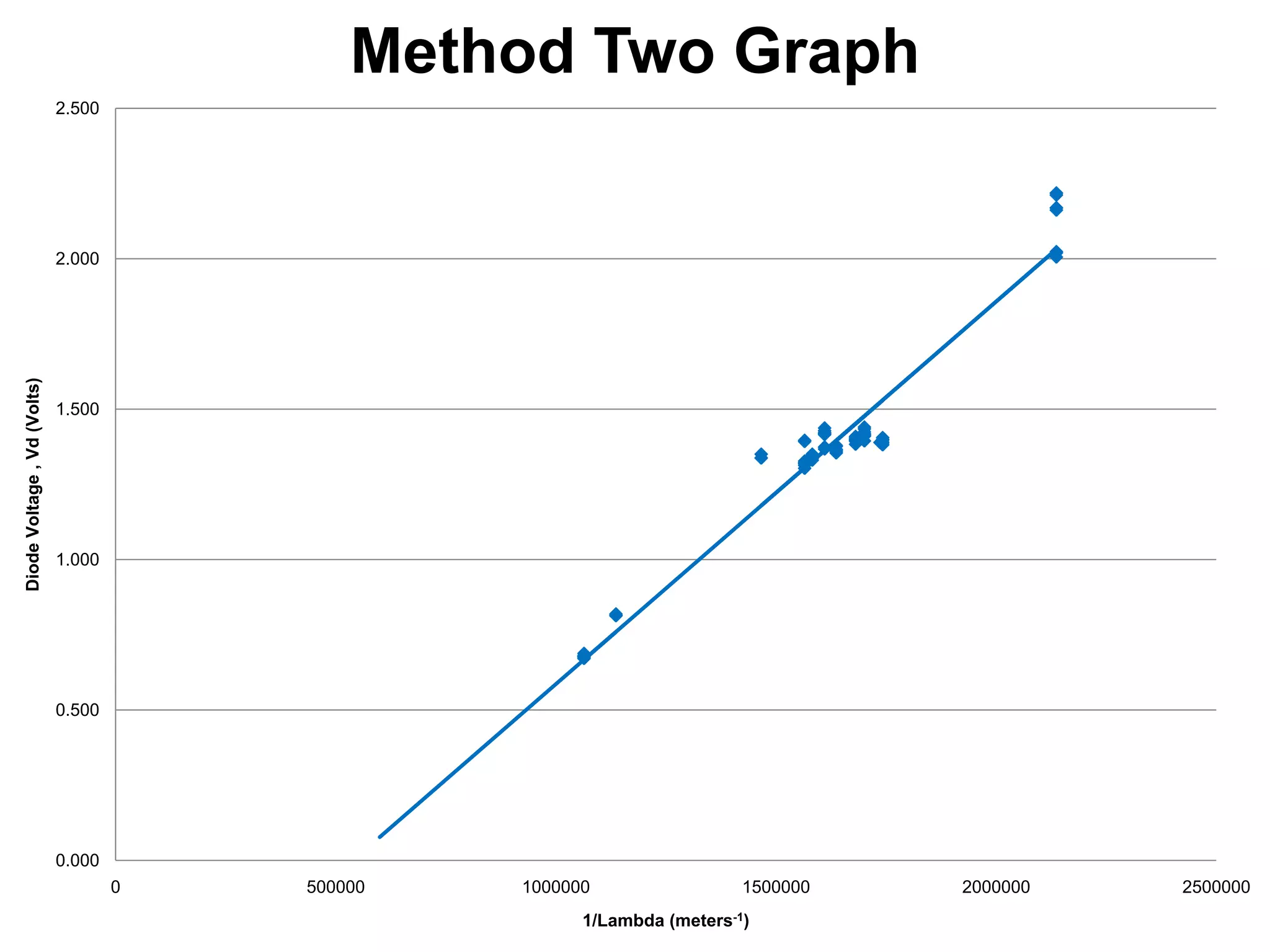
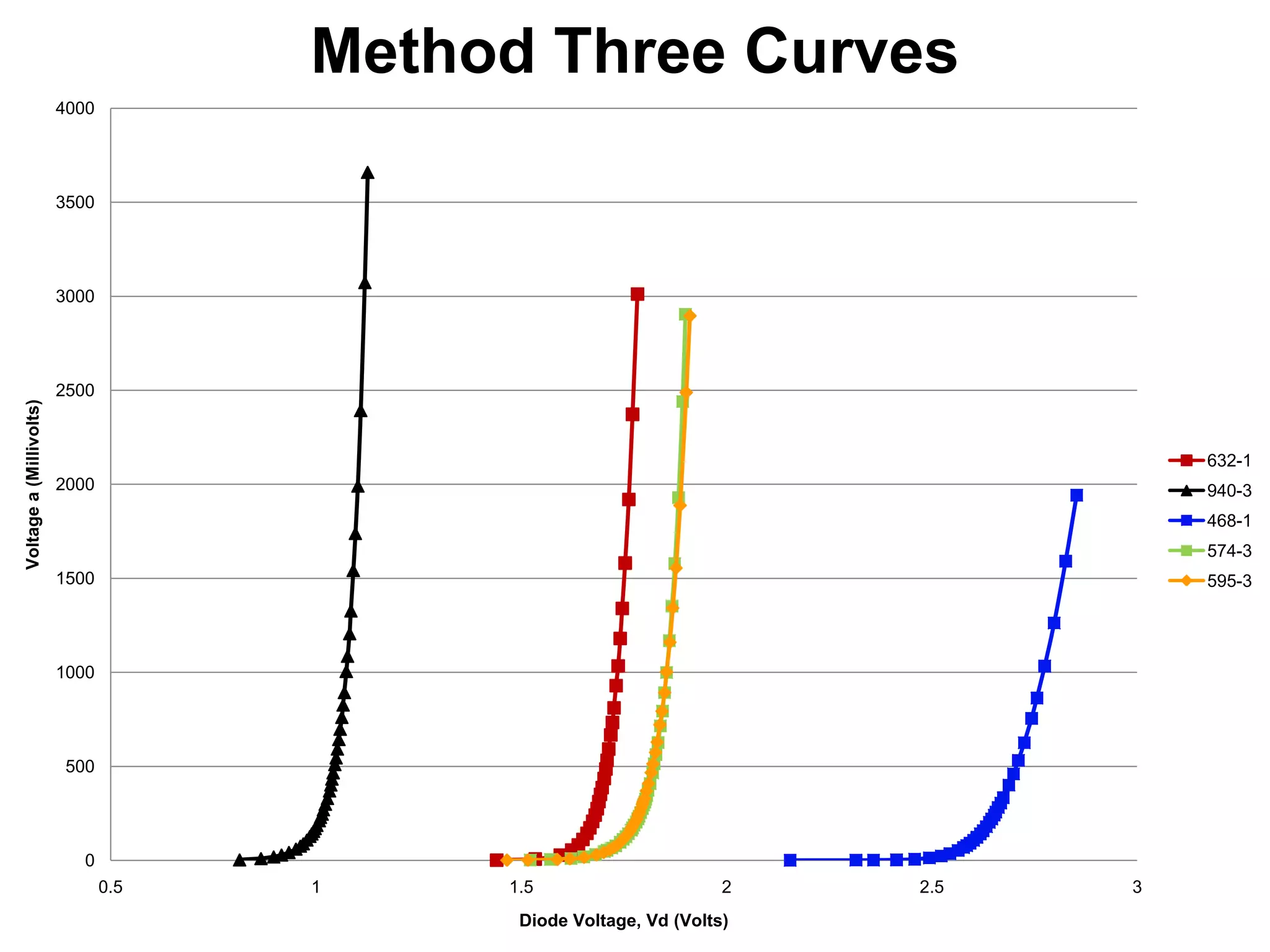
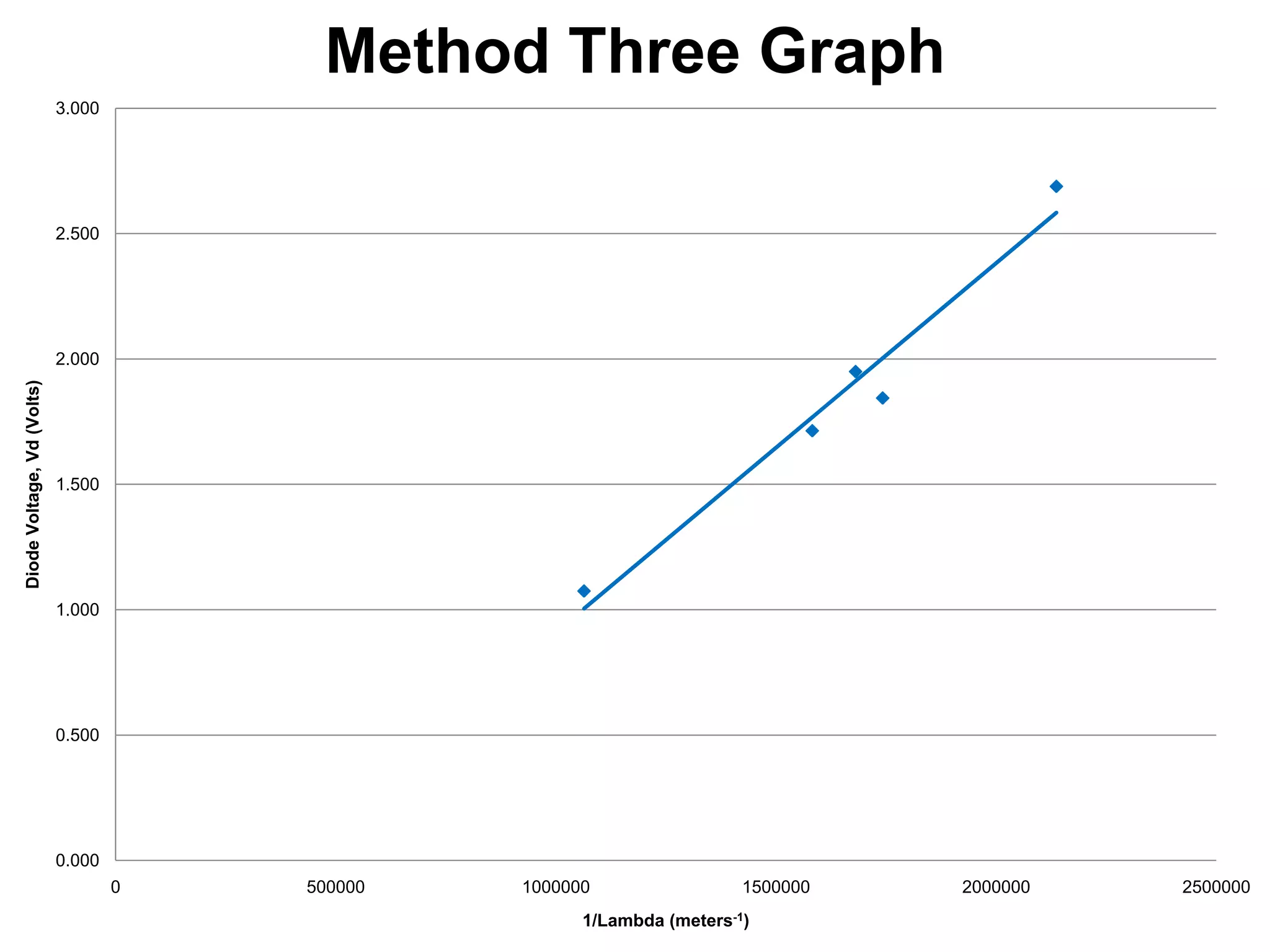
The document describes an experiment to measure Planck's constant using three different methods with LEDs of varying wavelengths. The first method observes the voltage when light first becomes visible. The second measures voltage when current begins to flow. The third graphs voltage and extrapolates the threshold. The author hypothesizes the second method will be most accurate since it relies solely on multimeter readings. Results show the second method was closest to the accepted value of Planck's constant, with the first and third methods less accurate due to human judgment factors.