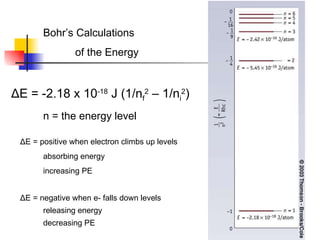
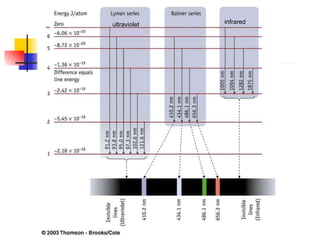
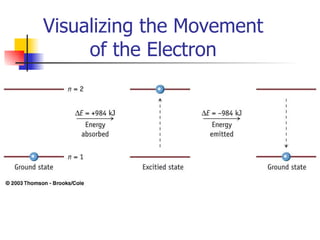
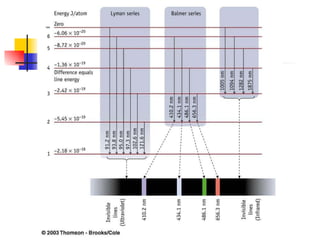
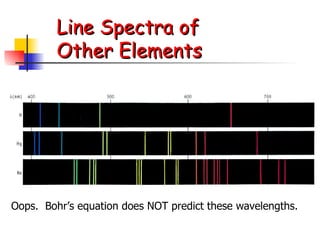
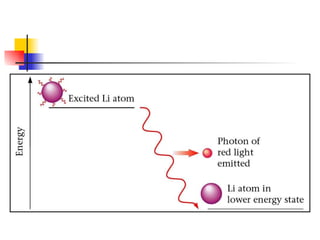
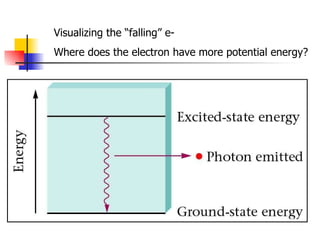
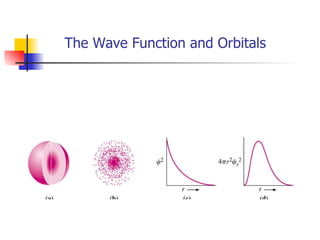
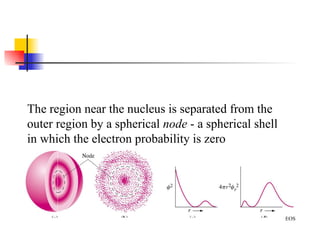
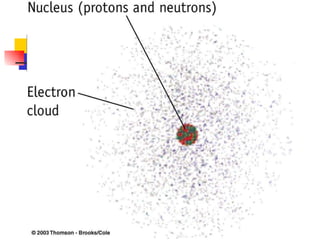
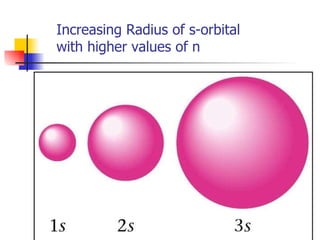
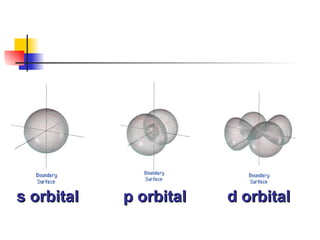
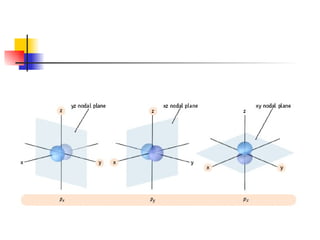
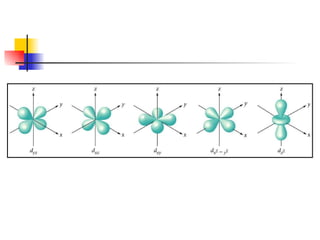
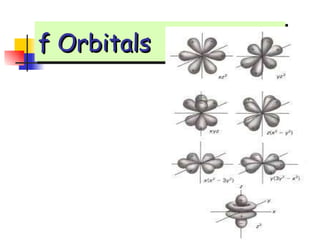
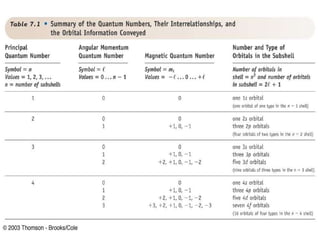
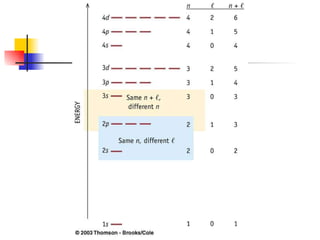
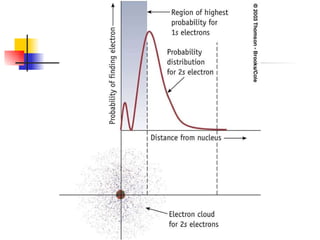
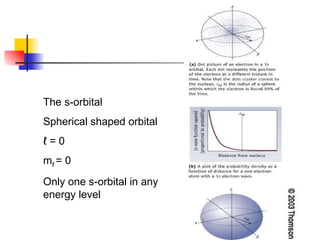
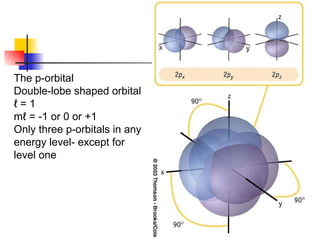
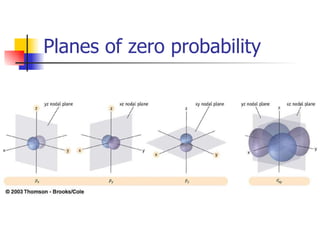
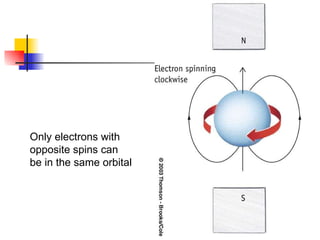
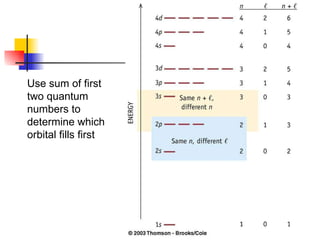
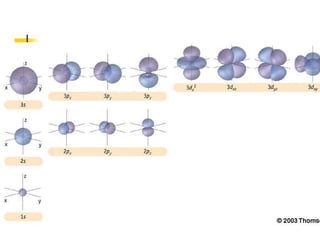
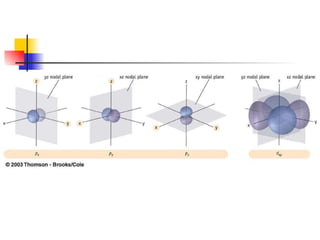
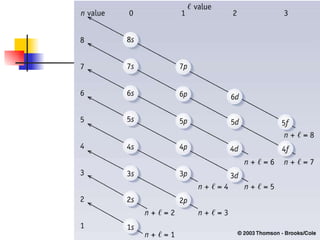
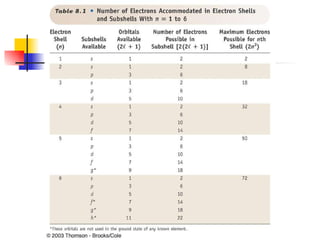
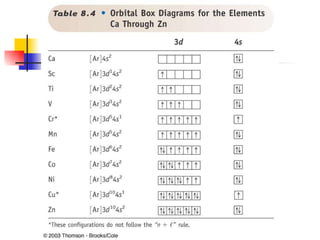
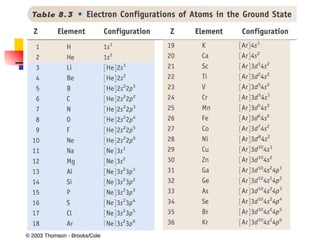
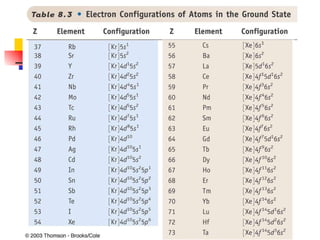
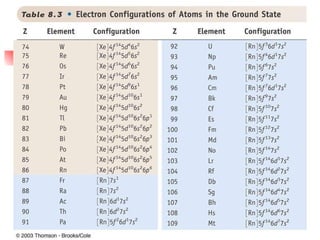
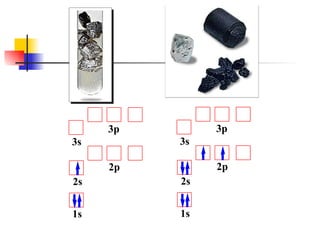
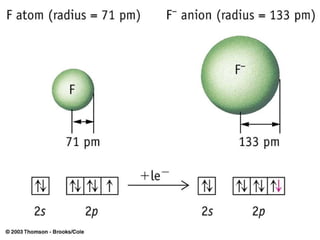
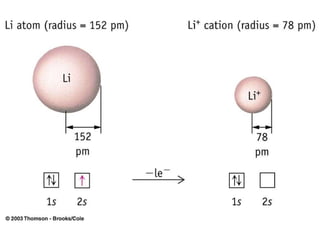
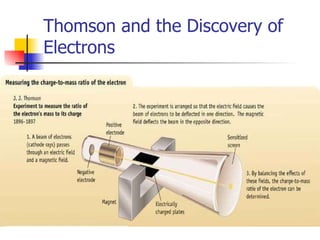
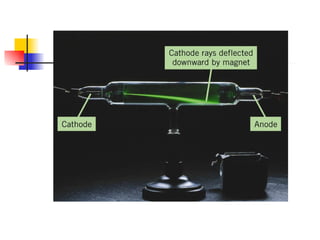
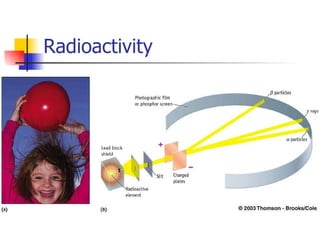
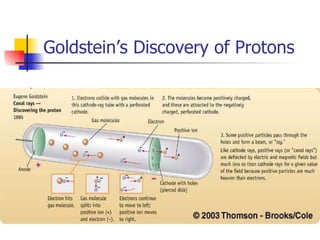
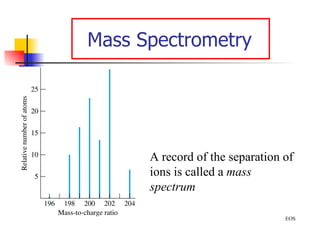
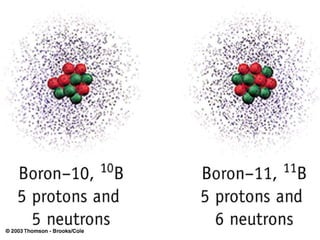
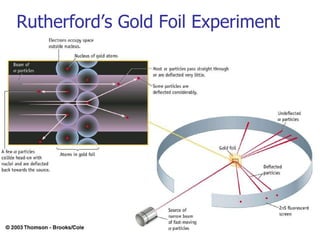
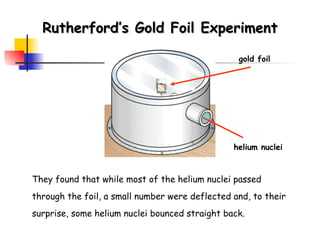
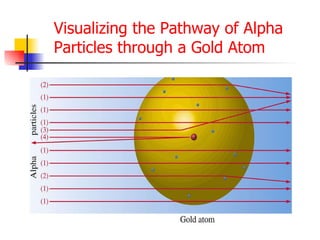
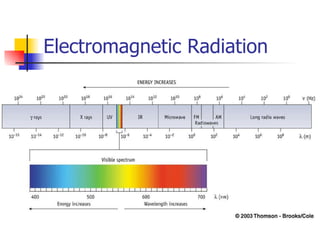
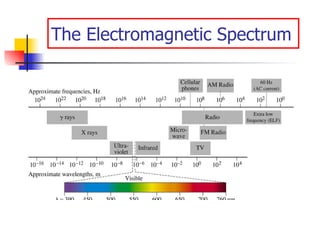
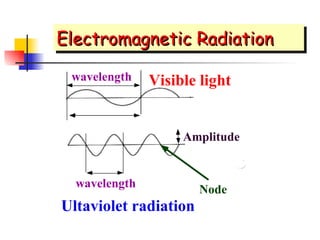
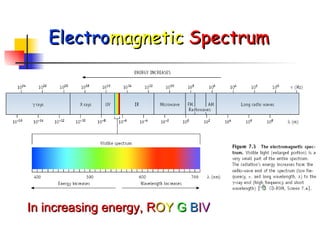
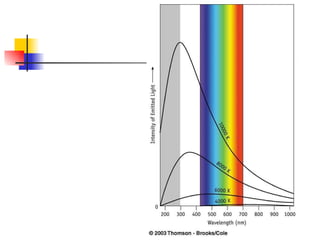
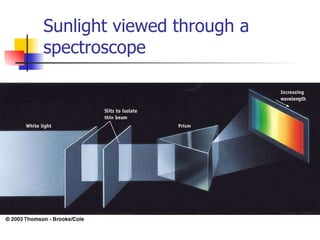
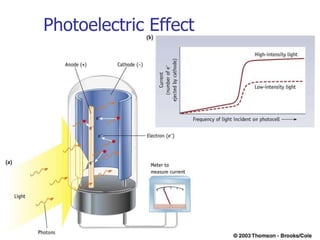
The document provides a history of the development of atomic structure models from ancient Greek philosophers' ideas of indivisible atoms to the modern quantum mechanical model. It describes key experiments and findings such as Thomson's discovery of electrons, Rutherford's gold foil experiment, and Bohr's model of electron orbits that led to modern atomic theory. The emission spectra of elements provided evidence that electrons exist in specific energy levels and orbitals within atoms.

1. Lab 9 Atomic Structure Emission Spectrum Electron Configuration

2. HISTORY OF THE ATOM 460 BC Democritus develops the idea of atoms he pounded up materials in his mortar and pestle until he had reduced them to smaller and smaller particles which he called ATOMS ( greek for indivisible )

3. Development of the Model of an Atom 400 BC Democritus – Particle Model Ancient Greek philosopher Proposes that matter is composed of smallest particles called atoms An idea with no evidence Aristotle – Continuous Model Alternative idea Continuous model of matter- no smallest piece

4. HISTORY OF THE ATOM 1808 John Dalton suggested that all matter was made up of tiny spheres that were able to bounce around with perfect elasticity and called them ATOMS

5. Dalton proposes Atomic Theory in 1803 Based upon experimental evidence All matter composed of atoms Atoms of same element have same mass and properties Atoms are neither created nor destroyed, they are rather simply rearranged in chemical reactions Evidence – Lavoiser- Conservation of Mass Compounds are composed of elements in simple whole number ratios Evidence – Proust

6. HISTORY OF THE ATOM 1898 Joseph John Thompson found that atoms could sometimes eject a far smaller negative particle which he called an ELECTRON

7. Thomson and the Discovery of Electrons

9. J. J. Thomson’s Experiment Devised an experiment to find the ratio of the cathode ray particle’s mass ( m e ) to the charge ( e ) m e / e = –5.686 x 10 –12 kg C –1

10. Thomson’s Plum Pudding Model Based upon the charge to mass ratio, the electron must be much smaller than the atom Proposed negative electrons embedded in positive matrix of atom

11. HISTORY OF THE ATOM Thomson develops the idea that an atom was made up of electrons scattered unevenly within an elastic sphere surrounded by a soup of positive charge to balance the electron's charge 1904 PLUM PUDDING MODEL

12. Millikan’s Oil Drop Experiment Measuring the Charge on an electron

13. Unstable Atoms and Radioactivity Atoms are not indestructible Atoms are composed of smaller particles Alpha particles – positively charged Beta particles – negatively charged Gamma rays – no charge

14. Radioactivity

15. Goldstein’s Discovery of Protons

16. Mass Spectrometer- Determining the Percent Abundance of Different Isotopes of same element

17. Mass Spectrometer If a stream of positive ions having equal velocities is brought into a magnetic field, the lightest ions are deflected the most, making a tighter circle

18. Mass Spectrometry EOS A record of the separation of ions is called a mass spectrum

19. Isotopes of Neon Neon-20 10 protons 10 neutrons Neon-21 10 protons 11 neutrons Neon-22 10 protons 12 neutrons

21. HISTORY OF THE ATOM 1910 Ernest Rutherford oversaw Geiger and Marsden carrying out his famous experiment. They fired Helium nuclei at a piece of gold foil which was only a few atoms thick. They found that although most of them passed through. About 1 in 10,000 hit

22. Rutherford’s Gold Foil Experiment

23. Rutherford’s Gold Foil Experiment gold foil helium nuclei They found that while most of the helium nuclei passed through the foil, a small number were deflected and, to their surprise, some helium nuclei bounced straight back.

24. Rutherford’s Nuclear Model of the Atom Most the alpha particles (helium nuclei) pass through the gold foil Atom mostly empty space Alpha particles did not hit anything A very few deflected straight back Alpha particles deflected by a dense positive nucleus

25. Visualizing the Pathway of Alpha Particles through a Gold Atom

26. ELECTROMAGNETIC RADIATION

27. Electromagnetic radiation.

28. Electromagnetic Radiation Most subatomic particles behave as PARTICLES and obey the physics of waves.

29. Electromagnetic Radiation

30. The Electromagnetic Spectrum

31. Wave Model of Light Wavelength  measured in meters (m) Frequency ƒ measured in waves per second (Hz) Energy E measured in Joules (J)

32. Wavelength, Frequency and Energy Wavelength inversely related to frequency Increasing wavelength  decreasing frequency Decreasing wavelength  increasing frequency Wavelength x frequency = speed of light c =  ƒ c = speed of light = 3.00 x 10 8 m/s Frequency directly related to energy Increasing frequency  increasing energy Energy = Planck’s constant x frequency E = h ƒ h = Planck’s constant = 6.63 x 10 -34 J/Hz

33. Electromagnetic Radiation wavelength Visible light wavelength Ultaviolet radiation Amplitude Node

34. Electro magnetic Spectrum In increasing energy, R O Y G B I V

36. Sunlight viewed through a spectroscope

37. Prisms and diffraction grating bend light Red light with longer wavelengths bend less Violet light with shorter wavelengths bend more Separates white light into ROYGBIV Red – Orange – Yellow – Green – Blue – Indigo – Violet long waves short waves low frequency high frequency low energy high energy

38. Photoelectric Effect

39. Photoelectric Effect Bright red light shined on the photocell has no effect- regardless of intensity or time Dim green light shined on the photocell causes electrons to be emitted and flow through the wire Brighter green light emits more electrons per second- greater current

40. Explaining the Photoelectric Effect ONLY the photon or particle model can be used to explain these results Energy is required to pull off negative electrons attracted to positive protons in nucleus- breaking attraction Each red photon does not have enough energy to pull off an electron – regardless of how long the light is shined Each green photon has more energy and can pull off the electron when the green photon collides

41. Light Spectrum Lab! Slit that allows light inside Line up the slit so that it is parallel with the spectrum tube (light bulb)

42. The Emission Spectrum of Hydrogen- Discrete Bands of Colored Light

43. Excited Gases & Atomic Structure

44. Emission Spectra of Different Atoms: A Fingerprint to Identify

45. Rydberg and Balmer (1886) Independently develop mathematical equations that fit the data for hydrogen emission spectrum The electron had no yet been discovered Neither had a model to explain the observed wavelengths Just an equation that worked

46. Rydberg Equation 1/ λ = R H [1/n 1 2 - 1/n 2 2 ] R H = 1.09678 x 10 -2 nm -1 Solve the equation for an electron moving from level 4 to 2.

47. Bohr’s Model of the Atom (1910) Assumed electrons orbit the nucleus in circular orbits Proposed the energy of the orbit is proportional to the distance from the nucleus (increasing distance – increasing energy) Assumed only certain allowable energies Used angular momentum to calculate the allowable energy

48. Bohr’s Model of the Atom (1910) When the atom absorbs energy Electron moves up to higher energy with more potential energy farther away from nucleus Unstable with higher PE Electron falls back down to lower levels Energy released PE converted to KE as electron fall The color of light observed reflects the energy released in the fall

49. Bohr’s Calculations of the Energy Δ E = -2.18 x 10 -18 J (1/n f 2 – 1/n i 2 ) n = the energy level Δ E = positive when electron climbs up levels absorbing energy increasing PE Δ E = negative when e- falls down levels releasing energy decreasing PE

50. Niels Bohr (1885-1962) Δ E = -2.18 x 10 -18 J (1/n f 2 – 1/n i 2 ) Calculate the energy as an electron drops from level 6 down to level 2. Calculate the frequency and wavelength of this photon.

51. ultraviolet infrared

52. Visualizing the Movement of the Electron

54. Line Spectra of Other Elements Oops. Bohr’s equation does NOT predict these wavelengths.

56. Visualizing the “falling” e- Where does the electron have more potential energy?

57. Electron is a wave - De Broglie De Broglie Since light is both particle and wave, perhaps so is matter both particle and wave Wavelength depends upon mass and velocity Objects with large mass have negligible, so small we can ignore Electrons with very small mass have wave properties that cannot be ignored λ = h/p

58. Quantum Mechanics Heisenberg Uncertainty principle Given the wavelike nature of electron Impossible to know both location and energy of electron Can only calculate the probable location Schrodinger Used calculus to “locate” the electron within orbital Orbitals – regions of space representing the most probable location of electron

59. E. Schrodinger 1887-1961 W. Heisenberg 1901-1976 Wave Functions: Calculating the Probability of locating an electron in a region of space The Uncertainty Principle: Cannot both determine location and energy of electron

60. The Wave Function and Orbitals

61. The region near the nucleus is separated from the outer region by a spherical node - a spherical shell in which the electron probability is zero EOS

63. Quantum Numbers Values that emerge from the wave functions of Schrodinger 1 st n = energy level 2 nd ℓ = shape of orbital (s, p, d or f) 3 rd m ℓ = orientation (diff versions) 4 th m s = magnetic spin of electron

64. Increasing Radius of s-orbital with higher values of n

65. s orbital p orbital d orbital

68. f Orbitals

72. The s-orbital Spherical shaped orbital ℓ = 0 m ℓ = 0 Only one s-orbital in any energy level

73. The p-orbital Double-lobe shaped orbital ℓ = 1 mℓ = -1 or 0 or +1 Only three p-orbitals in any energy level- except for level one

74. Planes of zero probability

75. Model of d-orbital

76. Only electrons with opposite spins can be in the same orbital

77. Electron Configurations Show the electrons in orbitals Box used to represent orbital Half arrow used to represent e- with opposite spins Electrons are placed in orbitals of lowest energy first

78. Use sum of first two quantum numbers to determine which orbital fills first

90. Nickel Electron Configuration and quantum numbers 1s 2s 2p 3s 3p 1 0 0 ½ 2 0 0 ½ 2 1 -1 ½ 2 1 0 ½ 3 0 0 ½ 3 1 0 ½ 2 1 0 ½ 3 1 -1 ½ 3 1 0 ½ 4s 3d 4 01 0 ½ 3 2 -2 ½ 3 2 -1 ½ 3 2 0 ½ 3 2 1 ½ 3 2 1 ½ 1 st # indicates energy level n = 1 1 st level n = 2 2 nd level 2 nd # type of orbital l = 0 is s-orbital l = 1 is p-orbital l = 2 is d-orbital