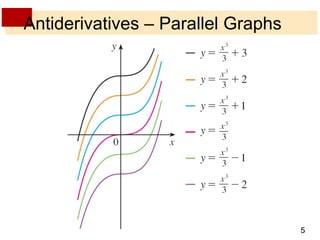
This document discusses antiderivatives and provides examples of finding antiderivatives of specific functions. It defines antiderivatives and notes their general form involves an arbitrary constant C. Example 1 finds the antiderivatives of sin x, 1/x, and x^n where n ≠ -1. It uses properties of derivatives and integral rules like the power rule to determine the antiderivatives are -cos x + C, ln|x| + C, and (x^(n+1))/(n+1) + C respectively. The document continues explaining using initial conditions to determine the value of C.

1. 4.8 Antiderivatives

2. 2
Antiderivatives - Definition

3. 3
Antiderivatives

4. 4
Antiderivatives – General Form

5. 5
Antiderivatives – Parallel Graphs

6. 6
Example 1
Find the most general antiderivative of each of the following
functions.
(a) f(x) = sin x (b) f(x) = 1/x (c) f(x) = xn, n ≠ –1
Solution:
(a) If F(x) = –cos x, then F(x) = sin x, so an antiderivative of
sin x is –cos x. By Theorem 1, the most general
antiderivative is G(x) = –cos x + C.
(b) Recall that

7. cont’d
7
Example 1 – Solution
So on the interval (0, ) the general antiderivative of 1/x
is ln x + C. We also learned that
for all x ≠ 0.
Theorem 1 then tells us that the general antiderivative of
f(x) = 1/x is ln |x| + C on any interval that doesn’t
contain 0.
In particular, this is true on each of the intervals ( , 0)
and (0, ).

8. 8
Example 1 – Solution
So the general antiderivative of f is
ln x + C1 if x > 0
ln(–x) + C2 if x < 0
(c) We use the Power Rule to discover an antiderivative of
xn. In fact, if n ≠ –1, then
cont’d
F(x) =

9. cont’d
9
Example 1 – Power Rule
Thus the general antiderivative of f(x) = xn is
This is valid for n  0 since then f(x) = xn is defined on an
interval. If n is negative (but n ≠ –1), it is valid on any
interval that doesn’t contain 0.

10. 10
Antiderivatives

11. 11
Antiderivatives - Excercises

12. 12
Find Function from 2nd Derivative

13. 13
Using Initial Conditions to find C

14. 14
Initial Conditions - Exercises