Visvesvaraya National Institute of Technology, Nagpur, Maharashtra, India, profile picture
Uploaded byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
PDF, PPTX2,169 views

Spatial filtering

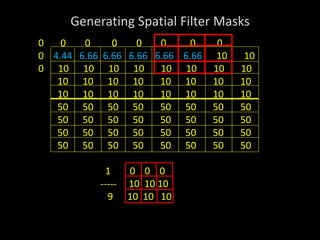
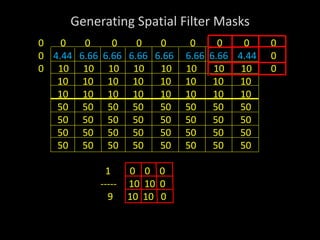
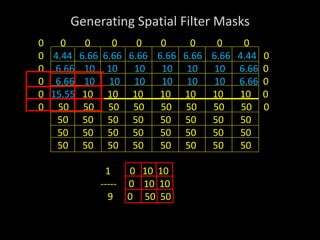
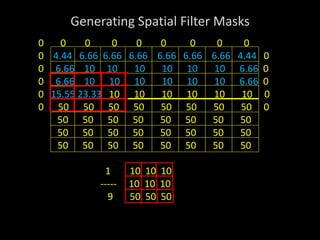
1) The document discusses spatial filtering of digital images, which refers to modifying images by applying filters in the spatial domain rather than the frequency domain. 2) Spatial filters are applied by using a kernel or mask over an image to perform operations on pixels within the mask's area. Common operations include averaging, edge detection, and noise removal. 3) A 3x3 mask is demonstrated as the simplest case, where the response value for the center pixel is the sum of the pixel values multiplied by the corresponding mask weights. This allows various filters to be generated for different purposes.

Embed presentation

Download as PDF, PPTX
DIGITAL IMAGE PROCESSING SPATIAL FILTERING by Dr. K. M. Bhurchandi
Fundamentals of Spatial Filtering • Filtering refers to accepting(passing) or rejecting certain frequency components. This effectively smoothens or sharpens the image. • E.g. Low pass filter, high pass filter, etc. • Such operations can be directly carried out on image in spatial domain also by using spatial filters (kernels, spatial masks, templates, & windows). • Spatial filters are more versatile as they are used in linear as well as non-linear filtering (Difficult in frequency domain).
Fundamentals of Spatial Filtering • Types of Spatial Filtering • 1) Point to point (pixel to pixel) operation (discussed so far) • 2) Mask based (Neighborhood) operations i) Operation with 3x3 filter (E.g. Mean, max, min, etc) ii) Correlation or Convolution • Linear vs Non-Linear Filter If the operation performed on the image pixels is linear, then the filter is called a linear spatial filter, otherwise nonlinear.
Operation with 3x3 Filter • At any point (x, y) in the image, the response, g(x, y), of the filter is the sum of products of the filter coefficients and the image pixels encompassed by the filter: g(x, y) = f(x-1,y-1).w1 + f(x-1,y).w2 + f(x-1,y+1).w3 + f(x,y-1).w4 + f( x, y).w5 + f(x,y+1).w6 + f(x+1,y-1).w7 + f(x+1,y).w8 + f(x+1,y+1).w9 • For the mask of size m x n, we assume m = 2a + 1; n = 2b + 1; where a & b are positive integers. • 3x3 is the smallest filter.
Operation with 3x3 Filter • Generalized equation: a b • g(x, y) = Σ Σ w(s, t) f(x + s, y + t) s = -a t = -b where, x & y are varied so that each pixel in w visits every pixel in f.
Operation with 3x3 Filter • 3 x 3 Neighborhood / Mask / Window / Template: (y - 1) y (y + 1) Y w(-1,-1) w(-1,0) w(-1,1) (x - 1) f(x-1, y-1) f(x-1, y) f(x-1, y+1) w(0,-1) w(0,0) w(0,1) x f(x, y-1) f(x, y) f(x, y+1) w(1,-1) w(1,0) w(1,1) (x + 1) f(x+1, y-1) f(x+1, y) f(x+1, y+1) X
Correlation & Convolution • Correlation & Convolution are two closely related concepts used in linear spatial filtering. • Correlation: It is a process of moving a filter mask over an image & computing the sum of products at each location. • Convolution: Here, the mechanics are same, except that the filter is first rotated by 180˚. • Correlation & Convolution are function of displacement. Correlation & Convolution are exactly same if the filter mask is symmetric. • 1D correlation and convolution of a filter with a discrete unit impulse is shown below.
Correlation & Convolution • Correlation is a function of displacement of the filter. • Correlating a filter w with a function that contains all ‘0’ & single ‘1’ yields a 180˚ rotated copy of w. • Correlating a function with discrete unit impulse yields a rotated (time inverted) version of the function. • Convolving a function with a unit impulse yields the same function. • Thus, to perform convolution all we have to do is rotate one function by 180˚ & perform same operation as in correlation.
Correlation & Convolution • Summarizing in equation form, we have that • The Correlation of a filter w(x, y) of size mxn with an image f(x, y)is given by: • The Convolution of w(x, y) and f(x, y) is given by:
Vector representation of Linear Filtering R = w1z1 + w2z2 + ….+w9z9 = 𝑤𝑘𝑧𝑘 9 𝑘=1 = wTz Where, w & z are 9-dimensional vectors formed from coefficients of the mask & image intensities encompassed by the mask, resp.
Generating Spatial Filter Masks 1) Average Mean Filter • The average value at any location (x, y) in the image is the sum of the nine intensity values in the 3 x 3 neighborhood centered on (x, y) divided by 9. • If zi, i = 1, 2, …, 9 denote these intensities, then the average is:
Generating Spatial Filter Masks General implementation for filtering an M x N image with a weighted average filter of size m x n is given by: 2) Exponential Filter • Some applications have a continuous function of 2 variables. E.g. Gaussian function Spatial filter mask has the basic form: where, σ is standard deviation
Generating Spatial Filter Masks Ex. 1) 8x8 Pseudo image with a single edge (High Frequency) of 10 & 50. Remove using a 3x3 size averaging mask. 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image
Generating Spatial Filter Masks 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 1 1 1 ----- 1 1 1 9 1 1 1
Generating Spatial Filter Masks 0 0 0 0 10 10 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 1 1 1 Yellow – Input Image pixels ----- 1 1 1 Red – Current pixel 9 1 1 1
Generating Spatial Filter Masks 0 0 0 0 4.44 10 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 0 10 10 9 0 10 10 Blue – Output Image pixels
Generating Spatial Filter Masks 0 0 0 0 0 4.44 6.66 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 4.44 6.66 6.66 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 10 10 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 0 9 10 10 0
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 10 0 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 10 10 ----- 0 10 10 9 0 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 10 0 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 10 0 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 10 10 10 9 10 10 10
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 10 10 10 10 10 10 10 0 0 50 50 50 50 50 50 50 50 0 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 10 10 ----- 0 10 10 9 0 50 50
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.33 10 10 10 10 10 10 0 0 50 50 50 50 50 50 50 50 0 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 10 10 10 9 50 50 50
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.3323.3323.33 23.33 23.33 23.33 15.55 0 0 24.44 36.66 50 50 50 50 50 50 0 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 50 50 50 9 50 50 50
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.3323.3323.33 23.33 23.33 23.33 15.55 0 0 24.44 36.6636.66 36.66 36.66 36.66 36.66 24.44 0 0 33.33 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 50 50 50 ----- 50 50 50 9 50 50 50
Generating Spatial Filter Masks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.3323.3323.33 23.33 23.33 23.33 15.55 0 0 24.44 36.6636.66 36.66 36.66 36.66 36.66 24.44 0 0 33.33 50 50 50 50 50 50 33.33 0 0 33.33 50 50 50 50 50 50 33.33 0 0 22.22 33.33 33.33 33.33 33.3333.33 33.33 22.22 0 0 0 0 0 0 0 0 0 0 1 50 50 0 ----- 50 50 0 9 0 0 0
Generating Spatial Filter Masks 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 23.33 23.3323.33 23.33 23.33 23.33 10 50 36.66 36.66 36.66 36.66 36.66 36.66 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 1 1 1 ----- 1 1 1 9 1 1 1
Generating Spatial Filter Masks  In the resultant image the Low frequency region has remained unchanged.  Sharp transition between 10 & 50 has changed from 10 to 23.33 to 36.66 and finally to 50.  Thus, Sharp edges has become blurred.  Best result when used over image corrupted by Gaussian noise.  Other types of low pass averaging mask are: 1 0 1 0 1 1 1 1 ---- 1 2 1 ---- 1 2 1 6 0 1 0 10 1 1 1
Order-Statistic Filters • These are non-linear spatial filters whose response is based on ordering (increasing / decreasing) the pixels contained in the image area encompassed by the filter. • Then replacing the value of the center with the middle value determined by ranking result. • E.g. Median filter, Max filter, Min Filter • i) Median Filter: • Popular with certain random noise and impulse noise (Salt & Pepper noise). – They provide excellent noise reduction – Comparatively less blurring than linear smoothing filter of same size.
Order-Statistic Filters Ex. 2) 8x8 Pseudo image with a single edge (High Frequency) of 10 & 50. Remove using a 3x3 size median filter mask. 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 250 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image
Order-Statistic Filters 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 250 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
Order-Statistic Filters 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 250 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
Order-Statistic Filters 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
Order-Statistic Filters 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
Order-Statistic Filters 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
Order-Statistic Filters 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
Order-Statistic Filters 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 Output Image
Order-Statistic Filters • ii) Max Filter: • It is used to find the brightest points in an image. – Response of a 3 x 3 max filter is given by • iii) Min Filter: – Used to find the darkest points in an image.
Sharpening Spatial Filter • The principal objective of sharpening is to highlight transitions in intensity. • Applications: Electronics Printing, Medical Imaging, Industrial Inspection, Autonomous guidance in military systems, etc. • Derivatives of a digital function are defined in terms of differences: • First Derivative: i) must be zero in areas of constant intensity. ii) must be nonzero at the onset of an intensity step / ramp. iii) Must be nonzero along ramps. • First order derivative of 1D function f(x) is difference:
Sharpening Spatial Filter • Second derivative: i) must be zero in constant areas ii) Must be nonzero at the onset and end of an intensity step / ramp iii) Must be zero along ramps of constant slope. • Second order derivative of f(x) as the difference:
The Laplacian • Isotropic Filter: They are rotation invariant. • Laplacian is simplest Isotropic derivative operator. It is defined as: • Laplacian is a linear operator.
The Laplacian • To express the equation in discrete form, • In x-direction, • In y-direction, • Thus, discrete Laplacian of 2 variables is,
The Laplacian • Filters to implement Laplacian:
The Laplacian • If background features need to be recovered by still preserving the sharpening effect of the Laplacian, then • The basic way to use the Laplacian for image sharpening is: Where, f(x, y) – input image g(x, y) – sharpened image c – (-1) or (+1) for filters with negative & positive center resp.
Unsharp Masking & Highboost Filtering • The process of subtracting an unsharp (smoothed) version of an image from the original image is called unsharp masking. • It consists of three steps: • i) Blur the original image. • ii) Subtract the blurred image from the original (results in mask). • iii) Add the mask to the original. where if, k = 1, unsharp masking, k > 1, highboost filtering, k < 1, de-emphasizes the contribution of unsharp mask.
Unsharp Masking & Highboost Filtering • Mechanics of unsharp masking
Using First-Order Derivative (Gradient) • First derivative are implemented using the magnitude of the gradient. • For image f(x, y), the gradient of f at (x, y) is given by: • This vector points in the direction of the greatest rate of change of f at (x, y). • Its magnitude is given by: • Sometimes
Using First-Order Derivative (Gradient) • Roberts operators • Sobel operators
Miscellaneous content Low Pass Median Filtering:  Averaging Filter removes the noise by blurring till it is no longer seen.  It blurs the edges too.  Bigger the averaging mass more the blurring.  Sometimes the image contains ‘salt & pepper noise’.  If averaging filter is used then it will remove the noise at the cost of ruined edges.  Thus a nonlinear filter Median filter is required.  They are also called as order statistics filter since their response is based on ordering or ranking of pixels contained within the mask.  Here we use a blank mask.
Miscellaneous content  Apply 3x3 median filter to find a new image. (w/o zero padding) 3 4 2 3 1 7 3 2 4 5 3 8 2 3 1 7 3x3 blank mask Noisy Image S & P noise
Miscellaneous content  Apply 3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 2 4 5 3 8 4 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7
Miscellaneous content  Apply 3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 3 2 4 5 3 8 4 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7 2) 2 2 3 3 3 4 5 7 8
Miscellaneous content  Apply 3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 3 2 4 5 3 8 4 3 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7 2) 2 2 3 3 3 4 5 7 8 3) 1 1 2 3 3 3 4 5 7
Miscellaneous content  Apply 3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 3 2 4 5 3 8 4 3 3 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7 2) 2 2 3 3 3 4 5 7 8 3) 1 1 2 3 3 3 4 5 7 4) 1 2 3 3 3 5 7 7 8
Miscellaneous content Ex. 3) If x = {2 3 4 3 4 5 6} & w = {-1 0 1}, perform median filtering. Size of mask is 1x3. Term ‘0’ indicates the position from where filtering starts. Soln: 2 3 4 3 4 5 6 -1 0 1 Border value: 2 2 3 4 3 4 5 6 -1 0 1 Median value {2 3 4}: 3 2 3 4 3 4 5 6 -1 0 1 Median value {3 3 4}: 3
Miscellaneous content 2 3 4 3 4 5 6 -1 0 1 Median value {3 4 4}: 4 2 3 4 3 4 5 6 -1 0 1 Median value {3 4 5}: 4 2 3 4 3 4 5 6 -1 0 1 Median value {4 5 6}: 5 2 3 4 3 4 5 6 -1 0 1 Border value: 6 Result: {2 3 3 4 4 5 6}
Miscellaneous content Ex 4). Find the median filtered image by 3x3 mask for the given image. 2 4 15 0 3 5 2 6 11 0 2 10 6 16 0 2
Miscellaneous content High Pass Filtering:  Retains HF component while eliminates LF components.  High passed image will have no background(Low freq region).  It will have enhanced edges.  Used to sharpen blurred images.  Process of mask moving on image is same only the mask coefficients change.  Mask coefficients should have positive value at centre and negative values elsewhere.  Sum of coefficients must be zero.  Since, it should give Zero after being placed on LP region.
Miscellaneous content High Pass Masks: 3x3 High pass masks -1 -1 -1 -1 8 -1 -1 -1 -1 0 -1 0 -1 -2 -1 -1 4 -1 -2 12 -2 0 -1 0 -1 -2 -1
Miscellaneous content Ex 5) 8x8 Pseudo image with a single edge (High Frequency) of 10 & 100. Remove LP using a 3x3 size High pass filter mask. 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100
Miscellaneous content 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-10-10-10-10-10+80 = 0 -1 8 -1 -1 -1 -1
Miscellaneous content 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-10-10-10-10-10+80 = 0 -1 8 -1 -1 -1 -1
Miscellaneous content 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-10-10-100-100-100+80 = -270 -1 8 -1 -1 -1 -1
Miscellaneous content 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-100-100-100-100-100+800 = +270 -1 8 -1 -1 -1 -1
Miscellaneous content 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -100-100-100-100-100-100-100-100+800 = 0 -1 8 -1 -1 -1 -1
Miscellaneous content 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -270 -270 -270 -270 -270 -270 -270 -270 270 270 270 270 270 270 270 270 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Note: -270 is replaced by 0.
Miscellaneous content Ex. 6) Obtain the digital negative of the following 8 bits per pixel image of fig.1. 121 205 217 156 151 2 1 2 2 1 139 127 157 117 125 2 3 4 5 2 252 117 236 138 142 6 2 7 6 0 227 182 178 197 242 2 6 6 5 1 201 106 119 251 240 0 3 2 2 1 fig. 1 fig. 2 Ex. 7) Perform intensity level (gray level) slicing on a 3 bpp image of fig. 2 . Let r1 = 3 & r2 = 5. Draw the modified image using with background & without background transformation.
Miscellaneous content Ex. 8) The image shown below has 8 different gray levels. Plot this image using only 4 gray levels. 0 1 1 1 1 4 1 1 2 3 2 2 1 1 2 2 3 3 1 2 4 6 2 3 1 2 4 2 4 4 1 2 3 7 2 5
Miscellaneous content 8 gray levels: 0 0 1 0 0 2 2 3 2 1 4 4 5 4 2 6 6 0 0 0 0 0 4 7 6 3 0 0 2 2 2 2 0 0 2 2 2 2 0 2 4 6 2 2 0 2 4 2 4 4 0 2 2 6 2 4

More Related Content

PDF
Frequency Domain FIltering.pdf
byMuhammad_Ilham_21
 
PPT
Spatial filtering
byshabanam tamboli
 
PPT
Spatial domain and filtering
byUniversity of Potsdam
 
PDF
UNIT-2 image enhancement.pdf Image Processing Unit 2 AKTU
byankushspencer015
 
PPT
Fields of digital image processing slides
bySrinath Dhayalamoorthy
 
PPT
Chapter 6 Image Processing: Image Enhancement
byVarun Ojha
 
PPTX
Digital Image Processing
byPreethiPreethi28
 
PPTX
Image processing second unit Notes
byAAKANKSHA JAIN
 
Frequency Domain FIltering.pdf
byMuhammad_Ilham_21
 
Spatial filtering
byshabanam tamboli
 
Spatial domain and filtering
byUniversity of Potsdam
 
UNIT-2 image enhancement.pdf Image Processing Unit 2 AKTU
byankushspencer015
 
Fields of digital image processing slides
bySrinath Dhayalamoorthy
 
Chapter 6 Image Processing: Image Enhancement
byVarun Ojha
 
Digital Image Processing
byPreethiPreethi28
 
Image processing second unit Notes
byAAKANKSHA JAIN
 

What's hot

PPT
6.frequency domain image_processing
byNashid Alam
 
PDF
Histogram processing
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PPT
Thresholding.ppt
byshankar64
 
PPT
Image segmentation
byMd Shabir Alam
 
PPTX
Chapter 8 image compression
byasodariyabhavesh
 
PPT
unit-3.ppt
bymeenalshanmuganathan
 
PPSX
Image Enhancement in Spatial Domain
byDr. A. B. Shinde
 
PPSX
Color Image Processing: Basics
byDr. A. B. Shinde
 
PPTX
Chapter 3 image enhancement (spatial domain)
byasodariyabhavesh
 
PPTX
Psuedo color
byMariashoukat1206
 
PPT
Chapter10 image segmentation
byasodariyabhavesh
 
PDF
Image segmentation
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PPTX
Module 31
byUllasSS1
 
PPT
Morphological Image Processing
bykumari36
 
PPT
Enhancement in spatial domain
byAshish Kumar
 
PPTX
Region based segmentation
byramya marichamy
 
PPTX
Image Filtering in the Frequency Domain
byAmnaakhaan
 
PPSX
Edge Detection and Segmentation
byDr. A. B. Shinde
 
PPTX
Image compression in digital image processing
byDHIVYADEVAKI
 
PPTX
Image segmentation in Digital Image Processing
byDHIVYADEVAKI
 
6.frequency domain image_processing
byNashid Alam
 
Histogram processing
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Thresholding.ppt
byshankar64
 
Image segmentation
byMd Shabir Alam
 
Chapter 8 image compression
byasodariyabhavesh
 
unit-3.ppt
bymeenalshanmuganathan
 
Image Enhancement in Spatial Domain
byDr. A. B. Shinde
 
Color Image Processing: Basics
byDr. A. B. Shinde
 
Chapter 3 image enhancement (spatial domain)
byasodariyabhavesh
 
Psuedo color
byMariashoukat1206
 
Chapter10 image segmentation
byasodariyabhavesh
 
Image segmentation
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Module 31
byUllasSS1
 
Morphological Image Processing
bykumari36
 
Enhancement in spatial domain
byAshish Kumar
 
Region based segmentation
byramya marichamy
 
Image Filtering in the Frequency Domain
byAmnaakhaan
 
Edge Detection and Segmentation
byDr. A. B. Shinde
 
Image compression in digital image processing
byDHIVYADEVAKI
 
Image segmentation in Digital Image Processing
byDHIVYADEVAKI
 

Similar to Spatial filtering

PPTX
spatial_filtering fundamentals from textbook
bylunalovegood66
 
PPTX
imge enhncement sptil filtering55555.pptx
byprojectsall
 
PPTX
7. image enhancement using spatial filtering
byMdFazleRabbi18
 
PPT
06 spatial filtering DIP
bybabak danyal
 
PPTX
SPATIAL FILTER
byshalet kochumuttath Shaji
 
PPTX
Spatial operation.ppt
byBhanubhakta Poudel
 
PPTX
Digital image processing img smoothning
byVinay Gupta
 
PPTX
2. filtering basics
byAtul Kumar Jha
 
PDF
DIP_Lecture6.pdf. jdowjwdieehekehdjejrejwhehr
bystudyd133
 
PPTX
SPATIAL FILTERING. FOR UNDERGRADUATE .pptx
bysatushisammur
 
PPTX
Image Restoration And Reconstruction
byAmnaakhaan
 
PDF
CSE367 Lecture- image sinal processing lecture
byFatmaNewagy1
 
PPT
05_Spatial_Filtering.ppt
bypawankamal3
 
PPT
Spatial filtering
bySanyam Agarwal
 
PPTX
Presentation
byVikash Kumar Das
 
PDF
Spatial Domain Filtering.pdf
byswagatkarve
 
PPTX
SPATIAL FILTERING IN IMAGE PROCESSING
bymuthu181188
 
PPT
Spatial filtering
byDeepikaT13
 
PDF
IVR - Chapter 2 - Basics of filtering I: Spatial filters (25Mb)
byCharles Deledalle
 
PPTX
Lec5_AIP [Spatial Filtering] (1).pptxt767686777
byHumaKashafKhan
 
spatial_filtering fundamentals from textbook
bylunalovegood66
 
imge enhncement sptil filtering55555.pptx
byprojectsall
 
7. image enhancement using spatial filtering
byMdFazleRabbi18
 
06 spatial filtering DIP
bybabak danyal
 
SPATIAL FILTER
byshalet kochumuttath Shaji
 
Spatial operation.ppt
byBhanubhakta Poudel
 
Digital image processing img smoothning
byVinay Gupta
 
2. filtering basics
byAtul Kumar Jha
 
DIP_Lecture6.pdf. jdowjwdieehekehdjejrejwhehr
bystudyd133
 
SPATIAL FILTERING. FOR UNDERGRADUATE .pptx
bysatushisammur
 
Image Restoration And Reconstruction
byAmnaakhaan
 
CSE367 Lecture- image sinal processing lecture
byFatmaNewagy1
 
05_Spatial_Filtering.ppt
bypawankamal3
 
Spatial filtering
bySanyam Agarwal
 
Presentation
byVikash Kumar Das
 
Spatial Domain Filtering.pdf
byswagatkarve
 
SPATIAL FILTERING IN IMAGE PROCESSING
bymuthu181188
 
Spatial filtering
byDeepikaT13
 
IVR - Chapter 2 - Basics of filtering I: Spatial filters (25Mb)
byCharles Deledalle
 
Lec5_AIP [Spatial Filtering] (1).pptxt767686777
byHumaKashafKhan
 

More from Visvesvaraya National Institute of Technology, Nagpur, Maharashtra, India

PDF
Wavelet transform
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PDF
Radon transform numerical & Fourier slice theorem
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PDF
Pixel relationships
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PDF
Morphological image processing
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PDF
Mathematical tools in dip
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PDF
Image transforms
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PDF
Image restoration and reconstruction
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
PDF
Image enhancement
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Wavelet transform
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Radon transform numerical & Fourier slice theorem
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Pixel relationships
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Morphological image processing
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Mathematical tools in dip
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Image transforms
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Image restoration and reconstruction
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 
Image enhancement
byVisvesvaraya National Institute of Technology, Nagpur, Maharashtra, India
 

Recently uploaded

PDF
Digital_Signal_Processing_for_FIR_filterspdf
bytunacevik03
 
PDF
Yes, we put AI agents in production. No, don't try this at home
byMarie-Alice Blete
 
PDF
Performance_Metrics_Evolution_DannyJiang
byDanny Jiang
 
PDF
A wire harness (also called a wiring harness or cable harness)
byabhinandankondekar2
 
PDF
Deterministic Finite Automata to Regular Expression Conversion.pdf
byNileshPardeshi28
 
PDF
UNIT02_TRE_GEOMETRIC DESIGN.pdf_________
byAaquib Ansari
 
PPTX
Atlassian for the New Age: Efficiency, Alignment & Collaboration at Scale
byAnanyaBanerjee57
 
PPTX
Symmetrical faults in power system .pptx
byRased Khan
 
PDF
lecture notes digital_design_examples.pdf
bygeekcooder2020
 
PPTX
Power Circuit Breakers and Substations .pptx
byJawadAmjad16
 
PDF
graph graph graph theory Graph presentation .pdf
bygeekcooder2020
 
PPTX
Ortho Graphic Projections for civil engineering.pptx
byUmairAli575718
 
PPTX
Design and Development of Friction Stir Welding joints of Aluminium and Coppe...
byNareshKumarSingh12
 
PPTX
CFP_Unit 5. Structure and Functions pptx
bypawarbhaktiit
 
PPTX
Steam Turbines basicsproperties power plant-1.pptx
byAjitParwani
 
PDF
BOE 2.1 Inch LCD 1600X1600 For VR AR Headset Smart Device
bySyluxdisplay
 
PDF
SURAJIT PARAMANIK_ME_3RD_THERMODYNAMICS.pdf
byastikparamanik1970
 
PPTX
Power Electronics_PE_lecture_10_presentation .pptx
bykavitabani2
 
PPTX
Solar PV An Essential Requirement in renewable energy based sources Industria...
byshilpashukla2025
 
PPTX
CFP_Unit 3 Decision Control and Looping Statements
bypawarbhaktiit
 
Digital_Signal_Processing_for_FIR_filterspdf
bytunacevik03
 
Yes, we put AI agents in production. No, don't try this at home
byMarie-Alice Blete
 
Performance_Metrics_Evolution_DannyJiang
byDanny Jiang
 
A wire harness (also called a wiring harness or cable harness)
byabhinandankondekar2
 
Deterministic Finite Automata to Regular Expression Conversion.pdf
byNileshPardeshi28
 
UNIT02_TRE_GEOMETRIC DESIGN.pdf_________
byAaquib Ansari
 
Atlassian for the New Age: Efficiency, Alignment & Collaboration at Scale
byAnanyaBanerjee57
 
Symmetrical faults in power system .pptx
byRased Khan
 
lecture notes digital_design_examples.pdf
bygeekcooder2020
 
Power Circuit Breakers and Substations .pptx
byJawadAmjad16
 
graph graph graph theory Graph presentation .pdf
bygeekcooder2020
 
Ortho Graphic Projections for civil engineering.pptx
byUmairAli575718
 
Design and Development of Friction Stir Welding joints of Aluminium and Coppe...
byNareshKumarSingh12
 
CFP_Unit 5. Structure and Functions pptx
bypawarbhaktiit
 
Steam Turbines basicsproperties power plant-1.pptx
byAjitParwani
 
BOE 2.1 Inch LCD 1600X1600 For VR AR Headset Smart Device
bySyluxdisplay
 
SURAJIT PARAMANIK_ME_3RD_THERMODYNAMICS.pdf
byastikparamanik1970
 
Power Electronics_PE_lecture_10_presentation .pptx
bykavitabani2
 
Solar PV An Essential Requirement in renewable energy based sources Industria...
byshilpashukla2025
 
CFP_Unit 3 Decision Control and Looping Statements
bypawarbhaktiit
 

Spatial filtering

  • 1.
    DIGITAL IMAGE PROCESSING SPATIALFILTERING by Dr. K. M. Bhurchandi
  • 2.
    Fundamentals of SpatialFiltering • Filtering refers to accepting(passing) or rejecting certain frequency components. This effectively smoothens or sharpens the image. • E.g. Low pass filter, high pass filter, etc. • Such operations can be directly carried out on image in spatial domain also by using spatial filters (kernels, spatial masks, templates, & windows). • Spatial filters are more versatile as they are used in linear as well as non-linear filtering (Difficult in frequency domain).
  • 3.
    Fundamentals of SpatialFiltering • Types of Spatial Filtering • 1) Point to point (pixel to pixel) operation (discussed so far) • 2) Mask based (Neighborhood) operations i) Operation with 3x3 filter (E.g. Mean, max, min, etc) ii) Correlation or Convolution • Linear vs Non-Linear Filter If the operation performed on the image pixels is linear, then the filter is called a linear spatial filter, otherwise nonlinear.
  • 4.
    Operation with 3x3Filter • At any point (x, y) in the image, the response, g(x, y), of the filter is the sum of products of the filter coefficients and the image pixels encompassed by the filter: g(x, y) = f(x-1,y-1).w1 + f(x-1,y).w2 + f(x-1,y+1).w3 + f(x,y-1).w4 + f( x, y).w5 + f(x,y+1).w6 + f(x+1,y-1).w7 + f(x+1,y).w8 + f(x+1,y+1).w9 • For the mask of size m x n, we assume m = 2a + 1; n = 2b + 1; where a & b are positive integers. • 3x3 is the smallest filter.
  • 5.
    Operation with 3x3Filter • Generalized equation: a b • g(x, y) = Σ Σ w(s, t) f(x + s, y + t) s = -a t = -b where, x & y are varied so that each pixel in w visits every pixel in f.
  • 6.
    Operation with 3x3Filter • 3 x 3 Neighborhood / Mask / Window / Template: (y - 1) y (y + 1) Y w(-1,-1) w(-1,0) w(-1,1) (x - 1) f(x-1, y-1) f(x-1, y) f(x-1, y+1) w(0,-1) w(0,0) w(0,1) x f(x, y-1) f(x, y) f(x, y+1) w(1,-1) w(1,0) w(1,1) (x + 1) f(x+1, y-1) f(x+1, y) f(x+1, y+1) X
  • 7.
    Correlation & Convolution •Correlation & Convolution are two closely related concepts used in linear spatial filtering. • Correlation: It is a process of moving a filter mask over an image & computing the sum of products at each location. • Convolution: Here, the mechanics are same, except that the filter is first rotated by 180˚. • Correlation & Convolution are function of displacement. Correlation & Convolution are exactly same if the filter mask is symmetric. • 1D correlation and convolution of a filter with a discrete unit impulse is shown below.
  • 9.
    Correlation & Convolution •Correlation is a function of displacement of the filter. • Correlating a filter w with a function that contains all ‘0’ & single ‘1’ yields a 180˚ rotated copy of w. • Correlating a function with discrete unit impulse yields a rotated (time inverted) version of the function. • Convolving a function with a unit impulse yields the same function. • Thus, to perform convolution all we have to do is rotate one function by 180˚ & perform same operation as in correlation.
  • 11.
    Correlation & Convolution •Summarizing in equation form, we have that • The Correlation of a filter w(x, y) of size mxn with an image f(x, y)is given by: • The Convolution of w(x, y) and f(x, y) is given by:
  • 12.
    Vector representation ofLinear Filtering R = w1z1 + w2z2 + ….+w9z9 = 𝑤𝑘𝑧𝑘 9 𝑘=1 = wTz Where, w & z are 9-dimensional vectors formed from coefficients of the mask & image intensities encompassed by the mask, resp.
  • 13.
    Generating Spatial FilterMasks 1) Average Mean Filter • The average value at any location (x, y) in the image is the sum of the nine intensity values in the 3 x 3 neighborhood centered on (x, y) divided by 9. • If zi, i = 1, 2, …, 9 denote these intensities, then the average is:
  • 14.
    Generating Spatial FilterMasks General implementation for filtering an M x N image with a weighted average filter of size m x n is given by: 2) Exponential Filter • Some applications have a continuous function of 2 variables. E.g. Gaussian function Spatial filter mask has the basic form: where, σ is standard deviation
  • 15.
    Generating Spatial FilterMasks Ex. 1) 8x8 Pseudo image with a single edge (High Frequency) of 10 & 50. Remove using a 3x3 size averaging mask. 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image
  • 16.
    Generating Spatial FilterMasks 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 1 1 1 ----- 1 1 1 9 1 1 1
  • 17.
    Generating Spatial FilterMasks 0 0 0 0 10 10 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 1 1 1 Yellow – Input Image pixels ----- 1 1 1 Red – Current pixel 9 1 1 1
  • 18.
    Generating Spatial FilterMasks 0 0 0 0 4.44 10 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 0 10 10 9 0 10 10 Blue – Output Image pixels
  • 19.
    Generating Spatial FilterMasks 0 0 0 0 0 4.44 6.66 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
  • 20.
    Generating Spatial FilterMasks 0 0 0 0 0 0 4.44 6.66 6.66 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
  • 21.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
  • 22.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
  • 23.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
  • 24.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 10 9 10 10 10
  • 25.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 10 10 10 10 10 10 10 10 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 0 0 ----- 10 10 0 9 10 10 0
  • 26.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 10 0 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 10 10 ----- 0 10 10 9 0 10 10
  • 27.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 10 0 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 10 10 10 9 10 10 10
  • 28.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 10 0 0 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 10 10 10 9 10 10 10
  • 29.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 10 10 10 10 10 10 10 0 0 50 50 50 50 50 50 50 50 0 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 0 10 10 ----- 0 10 10 9 0 50 50
  • 30.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.33 10 10 10 10 10 10 0 0 50 50 50 50 50 50 50 50 0 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 10 10 10 9 50 50 50
  • 31.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.3323.3323.33 23.33 23.33 23.33 15.55 0 0 24.44 36.66 50 50 50 50 50 50 0 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 10 10 10 ----- 50 50 50 9 50 50 50
  • 32.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.3323.3323.33 23.33 23.33 23.33 15.55 0 0 24.44 36.6636.66 36.66 36.66 36.66 36.66 24.44 0 0 33.33 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 50 50 50 ----- 50 50 50 9 50 50 50
  • 33.
    Generating Spatial FilterMasks 0 0 0 0 0 0 0 0 0 0 4.44 6.66 6.66 6.66 6.66 6.66 6.66 4.44 0 0 6.66 10 10 10 10 10 10 6.66 0 0 6.66 10 10 10 10 10 10 6.66 0 0 15.55 23.3323.3323.33 23.33 23.33 23.33 15.55 0 0 24.44 36.6636.66 36.66 36.66 36.66 36.66 24.44 0 0 33.33 50 50 50 50 50 50 33.33 0 0 33.33 50 50 50 50 50 50 33.33 0 0 22.22 33.33 33.33 33.33 33.3333.33 33.33 22.22 0 0 0 0 0 0 0 0 0 0 1 50 50 0 ----- 50 50 0 9 0 0 0
  • 34.
    Generating Spatial FilterMasks 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 23.33 23.3323.33 23.33 23.33 23.33 10 50 36.66 36.66 36.66 36.66 36.66 36.66 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 1 1 1 1 ----- 1 1 1 9 1 1 1
  • 35.
    Generating Spatial FilterMasks  In the resultant image the Low frequency region has remained unchanged.  Sharp transition between 10 & 50 has changed from 10 to 23.33 to 36.66 and finally to 50.  Thus, Sharp edges has become blurred.  Best result when used over image corrupted by Gaussian noise.  Other types of low pass averaging mask are: 1 0 1 0 1 1 1 1 ---- 1 2 1 ---- 1 2 1 6 0 1 0 10 1 1 1
  • 36.
    Order-Statistic Filters • Theseare non-linear spatial filters whose response is based on ordering (increasing / decreasing) the pixels contained in the image area encompassed by the filter. • Then replacing the value of the center with the middle value determined by ranking result. • E.g. Median filter, Max filter, Min Filter • i) Median Filter: • Popular with certain random noise and impulse noise (Salt & Pepper noise). – They provide excellent noise reduction – Comparatively less blurring than linear smoothing filter of same size.
  • 37.
    Order-Statistic Filters Ex. 2)8x8 Pseudo image with a single edge (High Frequency) of 10 & 50. Remove using a 3x3 size median filter mask. 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 250 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image
  • 38.
    Order-Statistic Filters 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 250 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
  • 39.
    Order-Statistic Filters 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 250 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
  • 40.
    Order-Statistic Filters 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
  • 41.
    Order-Statistic Filters 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
  • 42.
    Order-Statistic Filters 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 250 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
  • 43.
    Order-Statistic Filters 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 8x8 Image with blank mask
  • 44.
    Order-Statistic Filters 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 50 Output Image
  • 45.
    Order-Statistic Filters • ii)Max Filter: • It is used to find the brightest points in an image. – Response of a 3 x 3 max filter is given by • iii) Min Filter: – Used to find the darkest points in an image.
  • 46.
    Sharpening Spatial Filter •The principal objective of sharpening is to highlight transitions in intensity. • Applications: Electronics Printing, Medical Imaging, Industrial Inspection, Autonomous guidance in military systems, etc. • Derivatives of a digital function are defined in terms of differences: • First Derivative: i) must be zero in areas of constant intensity. ii) must be nonzero at the onset of an intensity step / ramp. iii) Must be nonzero along ramps. • First order derivative of 1D function f(x) is difference:
  • 47.
    Sharpening Spatial Filter •Second derivative: i) must be zero in constant areas ii) Must be nonzero at the onset and end of an intensity step / ramp iii) Must be zero along ramps of constant slope. • Second order derivative of f(x) as the difference:
  • 49.
    The Laplacian • IsotropicFilter: They are rotation invariant. • Laplacian is simplest Isotropic derivative operator. It is defined as: • Laplacian is a linear operator.
  • 50.
    The Laplacian • Toexpress the equation in discrete form, • In x-direction, • In y-direction, • Thus, discrete Laplacian of 2 variables is,
  • 51.
    The Laplacian • Filtersto implement Laplacian:
  • 52.
    The Laplacian • Ifbackground features need to be recovered by still preserving the sharpening effect of the Laplacian, then • The basic way to use the Laplacian for image sharpening is: Where, f(x, y) – input image g(x, y) – sharpened image c – (-1) or (+1) for filters with negative & positive center resp.
  • 53.
    Unsharp Masking &Highboost Filtering • The process of subtracting an unsharp (smoothed) version of an image from the original image is called unsharp masking. • It consists of three steps: • i) Blur the original image. • ii) Subtract the blurred image from the original (results in mask). • iii) Add the mask to the original. where if, k = 1, unsharp masking, k > 1, highboost filtering, k < 1, de-emphasizes the contribution of unsharp mask.
  • 54.
    Unsharp Masking &Highboost Filtering • Mechanics of unsharp masking
  • 55.
    Using First-Order Derivative(Gradient) • First derivative are implemented using the magnitude of the gradient. • For image f(x, y), the gradient of f at (x, y) is given by: • This vector points in the direction of the greatest rate of change of f at (x, y). • Its magnitude is given by: • Sometimes
  • 56.
    Using First-Order Derivative(Gradient) • Roberts operators • Sobel operators
  • 57.
    Miscellaneous content Low PassMedian Filtering:  Averaging Filter removes the noise by blurring till it is no longer seen.  It blurs the edges too.  Bigger the averaging mass more the blurring.  Sometimes the image contains ‘salt & pepper noise’.  If averaging filter is used then it will remove the noise at the cost of ruined edges.  Thus a nonlinear filter Median filter is required.  They are also called as order statistics filter since their response is based on ordering or ranking of pixels contained within the mask.  Here we use a blank mask.
  • 58.
    Miscellaneous content  Apply3x3 median filter to find a new image. (w/o zero padding) 3 4 2 3 1 7 3 2 4 5 3 8 2 3 1 7 3x3 blank mask Noisy Image S & P noise
  • 59.
    Miscellaneous content  Apply3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 2 4 5 3 8 4 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7
  • 60.
    Miscellaneous content  Apply3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 3 2 4 5 3 8 4 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7 2) 2 2 3 3 3 4 5 7 8
  • 61.
    Miscellaneous content  Apply3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 3 2 4 5 3 8 4 3 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7 2) 2 2 3 3 3 4 5 7 8 3) 1 1 2 3 3 3 4 5 7
  • 62.
    Miscellaneous content  Apply3x3 median filter to find a new image. 3 4 2 3 3 4 2 3 1 7 3 2 1 3 3 2 4 5 3 8 4 3 3 8 2 3 1 7 2 3 1 7 1) 1 2 3 3 3 4 4 5 7 2) 2 2 3 3 3 4 5 7 8 3) 1 1 2 3 3 3 4 5 7 4) 1 2 3 3 3 5 7 7 8
  • 63.
    Miscellaneous content Ex. 3)If x = {2 3 4 3 4 5 6} & w = {-1 0 1}, perform median filtering. Size of mask is 1x3. Term ‘0’ indicates the position from where filtering starts. Soln: 2 3 4 3 4 5 6 -1 0 1 Border value: 2 2 3 4 3 4 5 6 -1 0 1 Median value {2 3 4}: 3 2 3 4 3 4 5 6 -1 0 1 Median value {3 3 4}: 3
  • 64.
    Miscellaneous content 2 34 3 4 5 6 -1 0 1 Median value {3 4 4}: 4 2 3 4 3 4 5 6 -1 0 1 Median value {3 4 5}: 4 2 3 4 3 4 5 6 -1 0 1 Median value {4 5 6}: 5 2 3 4 3 4 5 6 -1 0 1 Border value: 6 Result: {2 3 3 4 4 5 6}
  • 65.
    Miscellaneous content Ex 4).Find the median filtered image by 3x3 mask for the given image. 2 4 15 0 3 5 2 6 11 0 2 10 6 16 0 2
  • 66.
    Miscellaneous content High PassFiltering:  Retains HF component while eliminates LF components.  High passed image will have no background(Low freq region).  It will have enhanced edges.  Used to sharpen blurred images.  Process of mask moving on image is same only the mask coefficients change.  Mask coefficients should have positive value at centre and negative values elsewhere.  Sum of coefficients must be zero.  Since, it should give Zero after being placed on LP region.
  • 67.
    Miscellaneous content High PassMasks: 3x3 High pass masks -1 -1 -1 -1 8 -1 -1 -1 -1 0 -1 0 -1 -2 -1 -1 4 -1 -2 12 -2 0 -1 0 -1 -2 -1
  • 68.
    Miscellaneous content Ex 5)8x8 Pseudo image with a single edge (High Frequency) of 10 & 100. Remove LP using a 3x3 size High pass filter mask. 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100
  • 69.
    Miscellaneous content 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-10-10-10-10-10+80 = 0 -1 8 -1 -1 -1 -1
  • 70.
    Miscellaneous content 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-10-10-10-10-10+80 = 0 -1 8 -1 -1 -1 -1
  • 71.
    Miscellaneous content 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-10-10-100-100-100+80 = -270 -1 8 -1 -1 -1 -1
  • 72.
    Miscellaneous content 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -10-10-10-100-100-100-100-100+800 = +270 -1 8 -1 -1 -1 -1
  • 73.
    Miscellaneous content 10 1010 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -1 -1 -1 -100-100-100-100-100-100-100-100+800 = 0 -1 8 -1 -1 -1 -1
  • 74.
    Miscellaneous content 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -270 -270 -270 -270 -270 -270 -270 -270 270 270 270 270 270 270 270 270 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Note: -270 is replaced by 0.
  • 75.
    Miscellaneous content Ex. 6)Obtain the digital negative of the following 8 bits per pixel image of fig.1. 121 205 217 156 151 2 1 2 2 1 139 127 157 117 125 2 3 4 5 2 252 117 236 138 142 6 2 7 6 0 227 182 178 197 242 2 6 6 5 1 201 106 119 251 240 0 3 2 2 1 fig. 1 fig. 2 Ex. 7) Perform intensity level (gray level) slicing on a 3 bpp image of fig. 2 . Let r1 = 3 & r2 = 5. Draw the modified image using with background & without background transformation.
  • 76.
    Miscellaneous content Ex. 8)The image shown below has 8 different gray levels. Plot this image using only 4 gray levels. 0 1 1 1 1 4 1 1 2 3 2 2 1 1 2 2 3 3 1 2 4 6 2 3 1 2 4 2 4 4 1 2 3 7 2 5
  • 77.
    Miscellaneous content 8 graylevels: 0 0 1 0 0 2 2 3 2 1 4 4 5 4 2 6 6 0 0 0 0 0 4 7 6 3 0 0 2 2 2 2 0 0 2 2 2 2 0 2 4 6 2 2 0 2 4 2 4 4 0 2 2 6 2 4