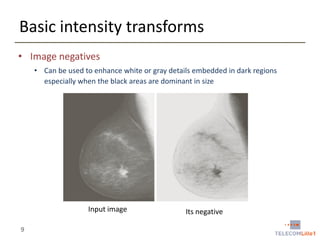
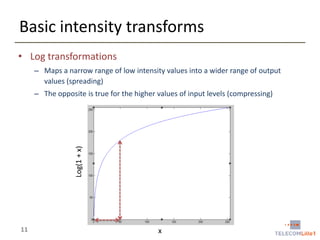
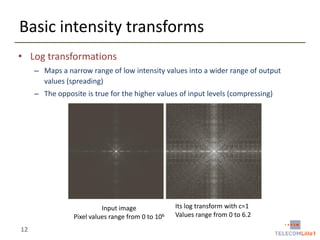
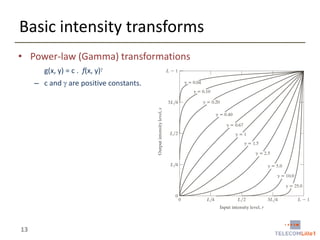
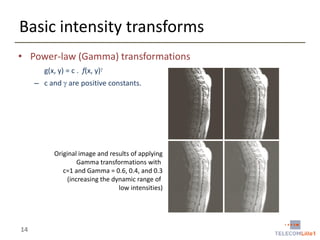
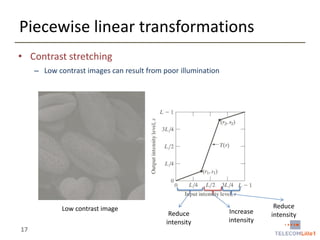
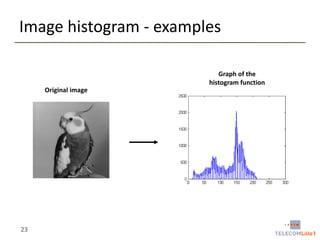
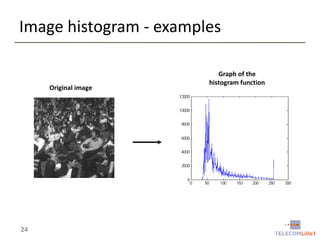
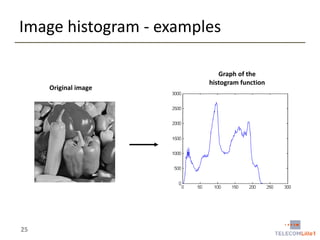
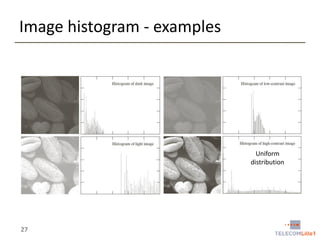
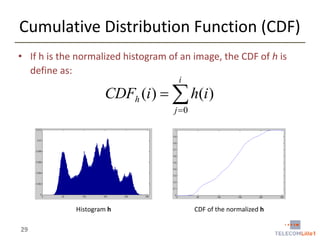
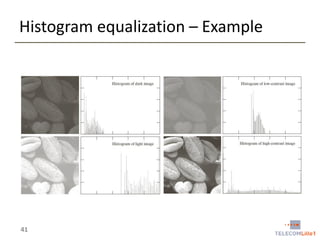
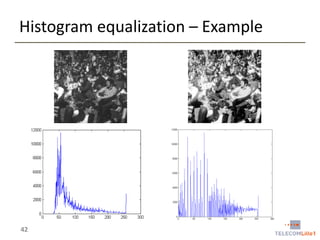
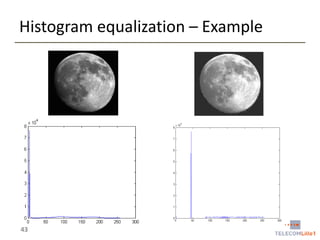
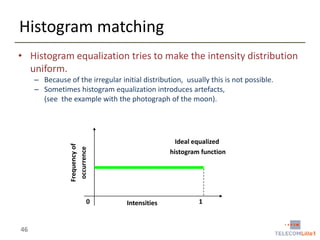
Digital Image Processing covers intensity transformations that can be performed on images. These include basic transformations like negatives, log transformations, and power-law transformations. It also discusses image histograms, which measure the frequency of each intensity level in an image. Histogram equalization aims to improve contrast by mapping intensities to produce a uniform histogram. It works by spreading out the most frequent intensity values.

1. Digital Image Processing
III. Intensity transformations
Hamid Laga
Institut Telecom / Telecom Lille1
hamid@img.cs.titech.ac.jp
http://www.img.cs.titech.ac.jp/~hamid/

2. In the previous lecture
• Colors
• The results of the interaction of light with the surface as observed by a
sensor from a viewing point
(the surface absorbs some light, depending on the material properties)
• Image
• a 2D function which encodes the color at each location of the image plane
• Digital image
• a 2D matrix, each entry is called a pixel, it can have a single value
(grayscale) or a vector of 3 values (color)
• Color spaces
• There are many color spaces, from now we will use the RGB color space.
• If we need to use another color space I will mention it explicitly
2

3. In the this lecture
• Basic processing operations that can be done on an image
•
3

4. Intensity transformations
• Outline
– Basic intensity transformations
(Image negatives, log transformations, power-law or Gamma
transformations)
– Image histogram
(Definitions, histogram equalization, local histogram processing,
histogram statistics for image enhancement)
– Your first TP (to be done in Matlab)
(Introduction to Matlab, Image manipulation with Matlab, …)
– Summary
4

5. Some definitions
• Spatial domain
• The image plane itself
• Processing in the spatial domain deals with direct manipulation of the
image pixels
• Other domains
• Frequency domain
• Consider the image as a 2D signal and apply Fourier transform
• Process the image in the transformed domain
• Apply the inverse transform to return into the spatial domain.
• Types of transformations that can be applied to an image
• Intensity transformations (this lecture)
• Operate on single pixels
• Spatial filtering (next lecture)
• Working on a neighborhood of every pixel
5

6. Basics
• Intensity transformation and spatial filtering
g ( x, y )  T  f ( x, y )
•
•
•
f : input image
g: output image
T: an operator applied to the image f
• In the discrete case
•
•
•
•
•
6
f and g are 2D matrices
of size WxH
T is a matrix of size wxh
which is much smaller than WxH
The value of each pixel of g is the result
of applying the operator T at the corresponding
location in f.
If wxh = 1x1  intensity transform
Otherwise, it’s spatial filtering.

7. Basic intensity transforms
• Definition
• g(x, y) = T (f(x, y))
• Examples
• Image negatives
• Log transformations
• Power-law (Gamma) transformations
• In the following
• Each image is represented with a 2D matrix of L intensity levels. That is each
pixel takes a value between 0 and L-1
7

8. Basic intensity transforms
• Image negatives
• Reversing the intensity levels
g(x, y) = L – 1 – f(x, y)
– It produces the equivalent of a photographic negatives
Input image
8
Its negative

9. Basic intensity transforms
• Image negatives
• Can be used to enhance white or gray details embedded in dark regions
especially when the black areas are dominant in size
Input image
9
Its negative

10. Basic intensity transforms
• Log transformations
g(x, y) = c . Log (1 + f(x, y))
– c is a constant and f(x, y) >= 0.
Input image
10
Its log transform c=1

11. Basic intensity transforms
• Log transformations
– Maps a narrow range of low intensity values into a wider range of output
values (spreading)
Log(1 + x)
– The opposite is true for the higher values of input levels (compressing)
11
x

12. Basic intensity transforms
• Log transformations
– Maps a narrow range of low intensity values into a wider range of output
values (spreading)
– The opposite is true for the higher values of input levels (compressing)
Input image
Pixel values range from 0 to 106
12
Its log transform with c=1
Values range from 0 to 6.2

13. Basic intensity transforms
• Power-law (Gamma) transformations
g(x, y) = c . f(x, y)
– c and  are positive constants.
13

14. Basic intensity transforms
• Power-law (Gamma) transformations
g(x, y) = c . f(x, y)
– c and  are positive constants.
Original image and results of applying
Gamma transformations with
c=1 and Gamma = 0.6, 0.4, and 0.3
(increasing the dynamic range of
low intensities)
14

15. Basic intensity transforms
• Power-law (Gamma) transformations
g(x, y) = c . f(x, y)
– c and  are positive constants.
Original image and results of applying
Gamma transformations with
c=1 and Gamma = 3, 4, and 5
(increasing the dynamic range of high
intensities)
15

16. Basic intensity transforms
• Piecewise linear transformation functions
– Piecewise linear functions can be arbitrary complex
 more flexibility in the design of the transformation
16

17. Piecewise linear transformations
• Contrast stretching
– Low contrast images can result from poor illumination
Low contrast image
17
Reduce
intensity
Increase
intensity
Reduce
intensity

18. Piecewise linear transformations
• Contrast stretching
– Low contrast images can result from poor illumination
Low contrast image
18
Contrast stretching

19. Intensity transformations
• Outline
– Basic intensity transformations
(Image negatives, log transformations, power-law or Gamma
transformations, piecewise-linear transformation functions)
– Image histogram
(Definitions, histogram equalization, histogram matching)
– Your first TP (to be done in Matlab)
(Introduction to Matlab, Image manipulation with Matlab, …)
– Summary
19

20. Image histogram - definitions
• Histogram
– The histogram function is defined over all possible
intensity levels.
– For each intensity level, its value is equal to the number of
the pixels with that intensity.
• Applications
– Image enhancement, compression, segmentation
– Very popular tool for realtime image processing
20

21. Image histogram - examples
• Consider the following 5x5 image
1
1
8
2
1
21
8
1
8
2
1
4
1
3
1
8
3
7
3
5
5
4
8
1
2
2

22. Image histogram - example
1
1
8
2
1
8
1
8
2
1
4
1
3
1
8
3
7
3
5
5
4
8
1
2
2
1
22
2
3
4
5
6
7
8

23. Image histogram - examples
Graph of the
histogram function
Original image
23

24. Image histogram - examples
Original image
24
Graph of the
histogram function

25. Image histogram - examples
Original image
25
Graph of the
histogram function

26. Image histogram - examples
Original image
26
Graph of the
histogram function

27. Image histogram - examples
Uniform
distribution
27

28. Image histogram - definitions
• Normalized histogram
– The normalised histogram function is the histogram function divided
by the total number of the pixels of the image
h( r )
p(r ) 
n
where n is the number of pixels in the image, and r is an intensity
level.
– It is the frequency of appearance of each intensity level (color) in the
image
– It gives a measure of how likely is for a pixel to have a certain intensity.
That is, it gives the probability of occurrence the intensity.
– The sum of the normalised histogram function over the range of all
intensities is 1.
28

29. Cumulative Distribution Function (CDF)
• If h is the normalized histogram of an image, the CDF of h is
define as:
i
CDFh (i )   h(i )
j 0
Histogram h
29
CDF of the normalized h

30. Histogram equalization
• Goal
• Increase the global contrast of an image by design a transformation (mapping) T
that that makes pixel intensities uniformly distributed over the whole range [0, L-1]
• Input
• An image f of intensity levels in [0, L-1]
• Intensity levels can be viewed as random variables
• Let’s hf be the normalized histogram of f.
hf is also the probability distribution function which we denote by Pf
• We denote by r intensity values of f
• Output
• An image g = T(f) such that the intensities of g are uniformly over the range [0, L1].
• This will improve the contrast by spreading out the most frequent intensity values
• We denote by s = T(r).
30

31. Review of probabilities
• Uniform probability distribution
• A probability distribution P is uniform if all events have the same probability of
occurrence.
• If N is the number of events then P(x) = 1 / N for every event x.
Frequency of
occurrence
Ideal equalized
histogram function
0
31
Intensities
1

32. Histogram equalization
• We want to compute
• An image g = T(f) such that the intensities of g are better distributed on the
histogram hg
• hg as a PDF, the intensities of g should follow a uniform distribution.
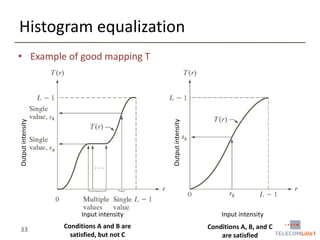
• Requirements for a good mapping T
• Condition A: T is required to be a monotonically increasing function in the
interval [0, L-1]
• That is if x < y  T(x) <= T(y)
• Avoids reversing intensities
• Condition B: x  [0, L-1]  T(x)  [0, L-1]
• This guarantees that the range of output intensities are the same as the range of input
intensities.
• Condition C: You may require strict monotonicity
• x < y  T(x) < T(y)
• This guarantees the mapping (or transformation )T is one-to-one.
32

33. Histogram equalization
Output intensity
Output intensity
• Example of good mapping T
Input intensity
33
Conditions A and B are
satisfied, but not C
Input intensity
Conditions A, B, and C
are satisfied

34. Histogram equalization
• Consider the following transformation
r
s  T (r )  ( L  1) p f (w)dw
0
• In the discrete case
r
s  T (r )  ( L  1) h f (r )
0
– That is, we add the values of the normalised histogram function from 1 to
k to find where the intensity will be mapped.
• This is the cumulative distribution function
• Short quiz:
• Prove that the transformation T defined as above satisfies the condition A
and condition B.
• Does it satisfy condition C?
34

35. Histogram equalization
• Solution to the Quiz
35

36. Histogram equalization
• Interesting property
• If we apply the transformation T to the image f we get an image g of
histogram hg such that
1
s [1, L  1], hg (s) 
L 1
• This is a uniform distribution !!!
36

37. Histogram equalization – Algorithm
• Input
• A discrete image f of L levels of intensity
• Algorithm
• Step1: Compute the normalized histogram hf of input image f
• Step 2: Compute the CDF of hf, denoted CDFhf
• Step 3: Find a transformation T: [0, L-1]  [0, L-1] such that
r
T (r )  ( L  1) h(q )  ( L  1)CDFhf (r )
q 0
• Step 4: Apply the transformation on each pixel of the input image f
• Propert ies
• The procedure is fully automatic and very fast
• Suitable for real-time applications
37

38. Histogram equalization – Example
• Do histogram equalization on the 5x5 image with integer
intensities in the range between one and eight
1
1
8
2
1
38
8
1
8
2
1
4
1
3
1
8
3
7
3
5
5
4
8
1
2
2

39. Histogram equalization – Example
• Do histogram equalization on the 5x5 image with integer
intensities in the range between one and eight
Normalised
histogram function
Intensity transformation function
p (r1 )  0.32
39
8
1
8
2
1
4
1
3
1
8
3
7
3
5
5
4
8
1
2
2
p (r2 )  0.16
T (r2 )  0.32  0.16  0.48
p (r3 )  0.12
T (r3 )  0.32  0.16  0.12  0.60
p (r4 )  0.08
T (r4 )  0.32  0.16  0.12  0.08  0.68
p (r5 )  0.08
T (r5 ) 
p (r6 )  0.00
T (r6 ) 
p (r7 )  0.04
T (r7 ) 
p (r8 )  0.20
1
1
8
2
1
T (r1 )  0.32
T (r8 ) 

40. Histogram equalization – Example
• Do histogram equalization on the 5x5 image with integer
intensities in the range between one and eight
Normalised
histogram function
Intensity
transformation function
p (r1 )  0.32
p (r2 )  0.16
T (r2 )  0.48
p (r3 )  0.12
T (r3 )  0.60
p (r4 )  0.08
T (r4 )  0.68
p (r5 )  0.08
T (r5 )  0.76
p (r6 )  0.00
T (r6 )  0.76
p (r7 )  0.04
T (r7 )  0.80
p (r8 )  0.20
40
T (r1 )  0.32
T (r8 )  1.00
The 32% of the pixels have intensity
r1. We expect them to cover 32% of
the possible intensities.
The 48% of the pixels have intensity
r2 or less. We expect them to cover
48% of the possible intensities.
The 60% of the pixels have intensity
r3 or less. We expect them to cover
60% of the possible intensities.
……………………………

41. Histogram equalization – Example
41

42. Histogram equalization – Example
42

43. Histogram equalization – Example
43

44. Histogram equalization of color images
• The above procedure is for grayscale images
• For color images
• Apply separately the procedure to each of the three channels
•  will yield in a dramatic change in the color balance
• NOT RECOMMENED unless you have a good reason for doing that.
• Recommended method
• Convert the image into another color space such as the Lab color space OR
HSL/HSV color space
• Apply the histogram equalization on the Luminance channel
• Convert back into the RGB color space.
44

45. Lab color space
• Lab color space is designed to approximate the human vision
• The L component matches the human perception of lightness
• The Lab space is much larger than the gamut of computer displays.
• Conversions
• Will be covered in a special lecture on Colors.
45

46. Histogram matching
• Histogram equalization tries to make the intensity distribution
uniform.
– Because of the irregular initial distribution, usually this is not possible.
– Sometimes histogram equalization introduces artefacts,
(see the example with the photograph of the moon).
Frequency of
occurrence
Ideal equalized
histogram function
0
46
Intensities
1

47. Histogram matching
• Instead
– We can specify the function we want for the histogram
Frequency of
occurrence
P: specified (target)
histogram
0
hf: initial (source)
histogram
1
Intensities
Find a transformation T such that the normalized
histogram of T(f) matches the probability distribution P.
P can be the normalized histogram of another image g,
then T transfers the histogram of g to f.
47

48. Histogram matching
• Goal
• Given an image f with a normalized histogram hf
• Given a probability distribution P
• Find a transformation T such that the normalized histogram of T(f)
matches the probability distribution P.
• Remarks
• If P is a uniform distribution then T is the same as the histogram
equalization.
48

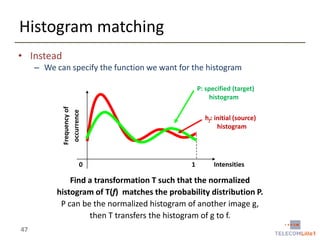
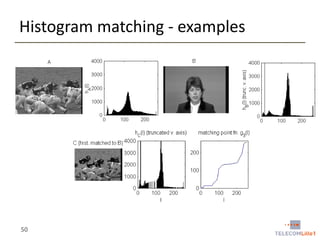
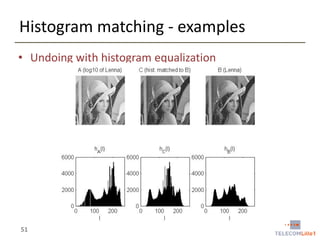
49. Histogram matching - procedure
• Input
• A source image f and a target distribution function P
• P can be the normalized histogram of another image g
• Procedure
• Calculate the histogram hf of f
• Calculate the CDFf of f and the CDFP of P
• For each gray level x  [0, L-1], find the gray level y for which
• CDFf(x) = CDFP(y)
• We denote this mapping by M
• Can be implemented as a lookup table
• Apply the mapping M to all pixels of the input image f
49

50. Histogram matching - examples
50

51. Histogram matching - examples
• Undoing with histogram equalization
51

52. Summary
• What we have seen
• Basic intensity transformations applied to individual pixels
• Histogram
• A very powerful tool in image processing
• A connection to probability and statistics
• Histogram equalization
• Histogram matching
• Enables the matching of the histogram of one image to the histogram of another
image
52

53. Next
• Spatial filtering, convolution, and enhancement
– Fundamentals
(Kernel, convolution, filtering)
– Smoothing
(Linear / non-linear filters)
– Sharpening
(The Laplacian - 2nd order derivatives, the gradient - first order
derivatives)
– Image pyramids
(The Gaussian pyramid)
– Filtering in the frequency domain
(just a short introduction)
53