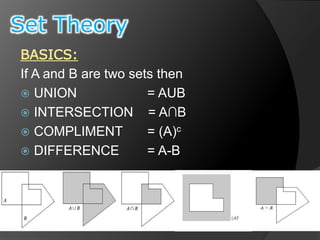
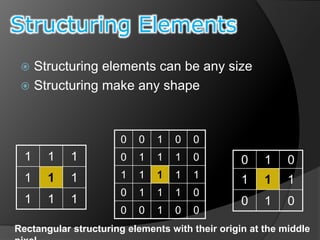
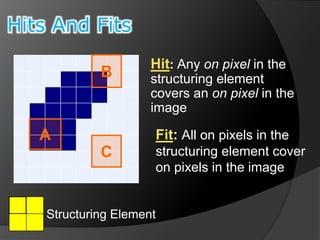
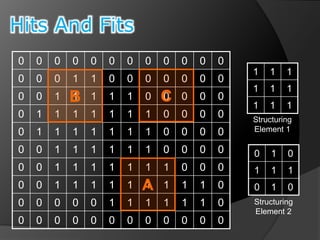
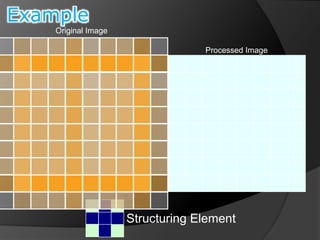
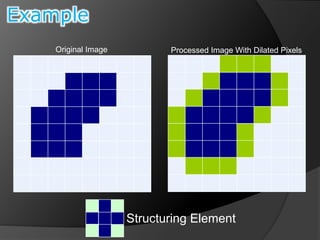
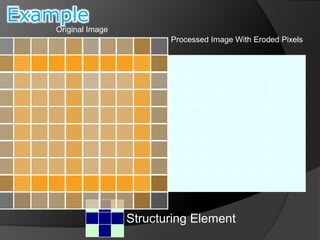
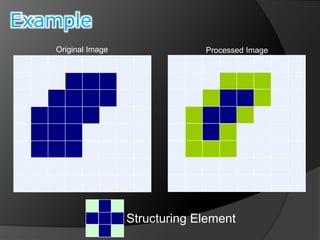
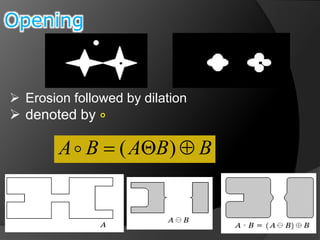
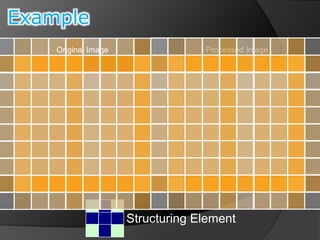
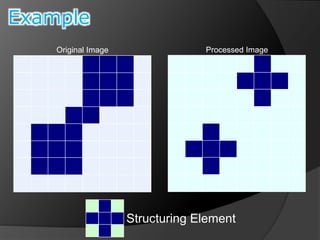
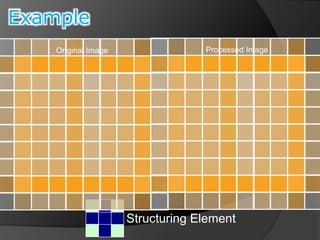
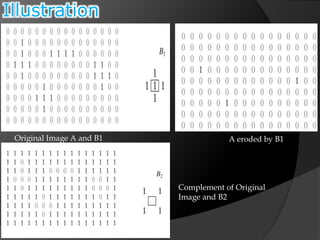
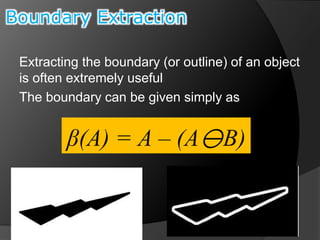
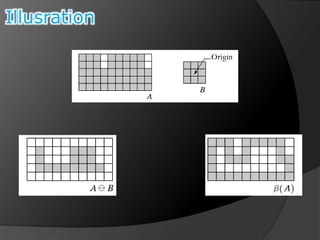
This document summarizes key concepts in morphological image processing including dilation, erosion, opening, closing, and hit-or-miss transformations. Morphological operations manipulate image shapes and structures using structuring elements based on set theory operations. Dilation adds pixels to the boundaries of objects in an image, while erosion removes pixels on object boundaries. Opening can remove noise and smooth object contours, while closing can fill in small holes and fill gaps in object shapes. Hit-or-miss transformations are used to detect specific patterns of on and off pixels. These operations form the basis for morphological algorithms like boundary extraction.

1. SEMINAR ON :
BY:
Raghukumar
D.S.

2. ABSTRCT
 Introduction
 Set Theory Concepts
 Structuring Elements , Hits or fits
 Dilation And Erosion
 Opening And Closing
 Hit-or-Miss Transformation
 Basic Morphological Algorithms
 Implementation
 Conclusion

3. Introduction
 Morphological – Shape , form , Structure
►Extracting and Describing image component
regions
►Usually applied to binary images
►Based on set Theory

4. Set Theory
BASICS:
If A and B are two sets then
 UNION = AUB
 INTERSECTION = A∩B
 COMPLIMENT = (A)c
 DIFFERENCE = A-B

5. BASIC LOGIC OPERATIONS :
A B A AND B
A.B
A OR B
A+B
NOT(A)
−
푨
0 0 0 0 1
0 1 0 1 1
1 0 0 1 0
1 1 1 1 0

6. LOGIC OPERATIONS REPRESENTATION:

7. Structuring Elements
 Structuring elements can be any size
 Structuring make any shape
1 1 1
1 1 1
1 1 1
0 0 1 0 0
0 1 1 1 0
1 1 1 1 1
0 1 1 1 0
0 0 1 0 0
0 1 0
1 1 1
0 1 0
Rectangular structuring elements with their origin at the middle
pixel

8. Hits And Fits
Hit: Any on pixel in the
structuring element
covers an on pixel in the
image
B
A
C
Fit: All on pixels in the
structuring element cover
on pixels in the image
Structuring Element

9. 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 0 0 0 0 0 0 0
0 0 1 B 1 1 1 1 0 C
0 0 0 0
0 1 1 1 1 1 1 1 0 0 0 0
0 1 1 1 1 1 1 1 0 0 0 0
0 0 1 1 1 1 1 1 0 0 0 0
0 0 1 1 1 1 1 1 1 0 0 0
0 0 1 1 1 1 1 A
1 1 1 1 0
0 0 0 0 0 1 1 1 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0
1 1 1
1 1 1
1 1 1
Structuring
Element 1
0 1 0
1 1 1
0 1 0
Structuring
Element 2
Hits And Fits

10. Dilation
Dilation of image f by structuring element s is given
by f s
The structuring element s is positioned with its origin
at (x, y) and the new pixel value is determined using
the rule:
1 if hits
  

0 otherwise
( , )
s f
g x y


11. Example
Structuring Element
Original Image
Processed Image

12. Original Image Processed Image With Dilated Pixels
Structuring Element
Example

13. Erosion
Erosion of image f by structuring element s is given
by f  s
The structuring element s is positioned with its
origin at (x, y) and the new pixel value is determined
using the rule:
  

1 if fits
0 otherwise
( , )
s f
g x y

14. Structuring Element
Original Image
Processed Image With Eroded Pixels
Example

15. Original Image Processed Image
Structuring Element
Example

16. Erosion v/s Dilation
Erosion
 removal of structures of
certain shape and size,
given by SE
 Erosion can split apart
Dilation
joined objects and strip
away extrusions
 filling of holes of
certain shape and
size, given by SE
 can repair breaks
and intrusions

17. Opening And Closing
 can be performed by performing combinations of
erosions and dilations
Combine to
keep general shape but
smooth with respect to
Opening object
Closing background

18. Opening
 Erosion followed by dilation
 denoted by ∘
A B  (AB) B

19. Original Image Processed Image
Structuring Element
Example

20. Original Image Processed Image
Structuring Element
Example

21. Closing
 Dilation followed by erosion
 denoted by •
f • s = (f s)s 

22. Original Image Processed Image
Structuring Element
Example

23. Original Image Processed Image
Structuring Element
Example

24. Opening V/S Closing
Opening
 AB is a subset
(subimage) of A
 If C is a subset of D,
then C B is a subset
of D B
 (A B) B = A B
Closing
 A is a subset
(subimage) of AB
 If C is a subset of D,
then C B is a subset
of D B
 (A B) B = A B
Note: repeated openings/closings has no effect!

25. Hit or Miss Transformation
Useful to identify specified configuration of pixels,
such as, isolated foreground pixels or pixels at end
of lines (end points)
A*B  (AB1)(AB2)

26. Illustration
Original Image A and B1 A eroded by B1
Complement of Original
Image and B2

27. Erosion of A complement
And B2
Intersection of eroded images

28. Morphological Algorithms
Using the simple technique we have
looked at so far we can begin to consider
some more interesting morphological
algorithms
We will look at:
 Boundary extraction

29. Boundary Extraction
Extracting the boundary (or outline) of an object
is often extremely useful
The boundary can be given simply as
β(A) = A – (AB)

30. Illusration

31. Example
A simple image and the result of
performing boundary extraction using a
square structuring element
Original Image Extracted Boundary

32. Conclusion
Morphology is powerful set of tools for extracting
features in an image
We implement algorithms like Thinning thickening
Skeletons etc. various purpose of image
processing activities like semantation.

33. Thank you