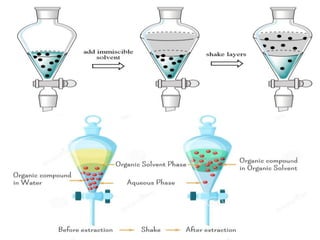
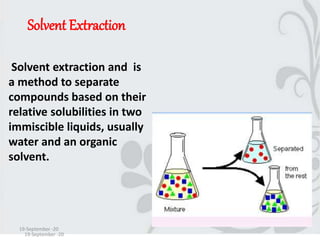
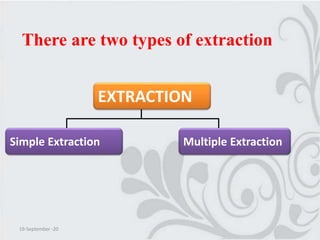
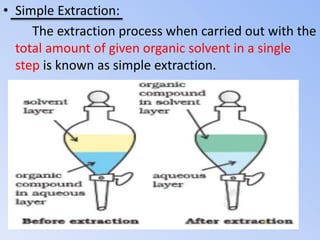
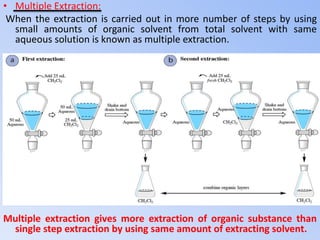
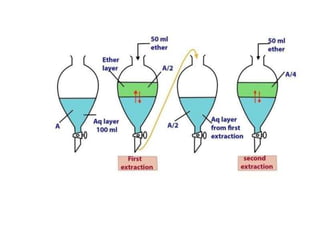
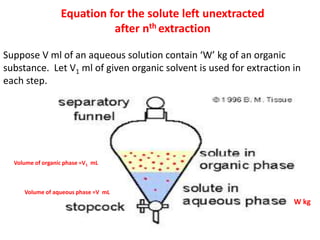
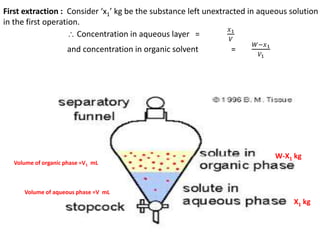
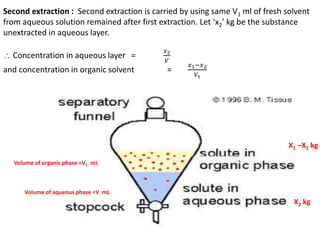
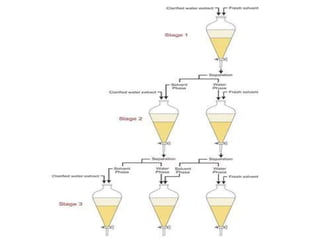
This document discusses solvent extraction, which uses the relative solubilities of compounds in immiscible liquids like water and an organic solvent to separate mixtures. It defines simple extraction as a single step process using the total solvent amount, while multiple extraction uses smaller portions of solvent over multiple steps. An equation is provided to calculate the amount of solute left unextracted after the nth extraction step based on the distribution coefficient K, volumes of solvents V and V1, and initial solute amount W. Two example problems demonstrate using this equation to determine extraction amounts for given conditions.

1. Dr. Y. S. THAKARE
M.Sc. (CHE) Ph D, NET, SET
Assistant Professor in Chemistry,
Shri Shivaji Science College, Amravati
Email: yogitathakare_2007@rediffmail.com
B Sc- II Year
SEM-III
PAPER-III
PHYSICAL CHEMISTRY
UNIT- V -PHASE EQUILIBRIUM
Topic- Application of Nernst Distribution Law
Solvent Extraction
25-September -20 1

2. Extraction
The most important application of distribution law
in industry as well as laboratory is the extraction.
Extraction (removal by a solvent) of an organic substance
from an aqueous solution. The process is carried by
shaking the aqueous solution with a immiscible organic
solvent, say ether in a separating funnel.
The distribution ratio of most of the organic
compounds is very large in favour of organic solvents. On
standing, the aqueous and ether layers separate in the
funnel. Ether layer is separated and applied to distillation.
The organic substance remains as residue in the flask.

4. Solvent Extraction
Solvent extraction and is
a method to separate
compounds based on their
relative solubilities in two
immiscible liquids, usually
water and an organic
solvent.
19-September -20
19-September -20

5. EXTRACTION
Simple Extraction Multiple Extraction
There are two types of extraction
19-September -20

6. • Simple Extraction:
The extraction process when carried out with the
total amount of given organic solvent in a single
step is known as simple extraction.

7. • Multiple Extraction:
When the extraction is carried out in more number of steps by using
small amounts of organic solvent from total solvent with same
aqueous solution is known as multiple extraction.
Multiple extraction gives more extraction of organic substance than
single step extraction by using same amount of extracting solvent.

9. Equation for the solute left unextracted
after nth extraction
Suppose V ml of an aqueous solution contain ‘W’ kg of an organic
substance. Let V1 ml of given organic solvent is used for extraction in
each step.
Volume of aqueous phase =V mL
Volume of organic phase =V1 mL
W kg

10. First extraction : Consider ‘x1’ kg be the substance left unextracted in aqueous solution
in the first operation.
 Concentration in aqueous layer =
𝑥1
𝑉
and concentration in organic solvent =
𝑊−𝑥1
𝑉1
Volume of aqueous phase =V mL
Volume of organic phase =V1 mL
X1 kg
W-X1 kg

11. From distribution law
𝐾 =
𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛 𝑖𝑛 𝑎𝑞𝑢𝑒𝑜𝑢𝑠 𝑝ℎ𝑎𝑠𝑒
𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛 𝑖𝑛 𝑜𝑟𝑔𝑎𝑛𝑖𝑐 𝑝ℎ𝑎𝑠𝑒
=
𝑥1
𝑉
𝑊 − 𝑥1
𝑉1
=
𝑥1𝑉1
𝑉(𝑊 − 𝑥1)
OR 𝐾𝑉𝑊 − 𝐾𝑉𝑥1 = 𝑥1𝑉1
𝐾𝑉𝑊 = 𝑥1𝑉1 + 𝐾𝑉𝑥1
𝐾𝑉𝑊 = 𝑥1(𝑉1+𝐾𝑉)
𝑥1 = 𝑊 (
𝐾𝑉
𝑉1+𝐾𝑉
) …..(1)

12. Second extraction : Second extraction is carried by using same V1 ml of fresh solvent
from aqueous solution remained after first extraction. Let ‘x2’ kg be the substance
unextracted in aqueous layer.
 Concentration in aqueous layer =
𝑥2
𝑉
and concentration in organic solvent =
𝑥1−𝑥2
𝑉1
Volume of aqueous phase =V mL
Volume of organic phase =V1 mL
X2 kg
X1 –X2 kg

13. From distribution law
𝐾 =
𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛 𝑖𝑛 𝑎𝑞𝑢𝑒𝑜𝑢𝑠 𝑝ℎ𝑎𝑠𝑒
𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛 𝑖𝑛 𝑜𝑟𝑔𝑎𝑛𝑖𝑐 𝑝ℎ𝑎𝑠𝑒
=
𝑥2
𝑉
𝑥1 −𝑥2
𝑉1
=
𝑥2𝑉1
𝑉(𝑥1−𝑥2)
OR 𝐾𝑉𝑥1 − 𝐾𝑉𝑥2 = 𝑥2𝑉1
𝐾𝑉𝑥1 = 𝑥2𝑉1 + 𝐾𝑉𝑥2
𝐾𝑉𝑥1 = 𝑥2(𝑉1+𝐾𝑉)
𝑥2 = 𝑥1 (
𝐾𝑉
𝑉1+𝐾𝑉
) ………(2)
𝑥2 = 𝑊
𝐾𝑉
𝑉1 + 𝐾𝑉
(
𝐾𝑉
𝑉1 + 𝐾𝑉
)
𝑥2 = 𝑊
𝐾𝑉
𝑉1+𝐾𝑉
2
…..(3)

14. 3) nth extraction : Similar to 2nd extraction, n-extractions are
carried out. Let ‘xn’ kg be the solute unextracted, then we get,
𝑥𝑛 = 𝑊
𝐾𝑉
𝑉1+𝐾𝑉
𝑛
………(4)

15. Problem :10 The distribution co-efficient of an alkaloid
between chloroform and water is 20 in favour of chlor oform.
Compare the weights of the alkaloid remaining in 100 ml
aqueous solution containing 1 gram when shaken with (a)
100 ml chloroform and (b) two successive 50 ml portions.
Solution :
K = C water 1
Csolvent 20

a) V = 100 ml
V1 = 100 ml
W = 1 g and n = 1
 1
1
KV
x W
KV V
 
  

 
1
100
20
1
1
100 100
20

 
 
= 0.0476 g
b) V = 100 ml
V1 = 50 ml
W = 1 g and n = 2
2
2
1
KV
x W
KV V
 
  

 
2
2
1
100
20
x 1
1
x100 50
20
 

 
  

 
 
= 0.0083 g
Hence the solute remained unextracted is more in case
(a) than case (b).

16. Problem : 11 An aqueous 0.1 dm3
solution of organic
compound contains 0.01 Kg of compound would be
extracted in five instalments of 0.02 dm3
each of
ether. If the partition coefficient is 5 in favour of
ether, calculate the amount extracted.
Solution :
K = Concentration of water 1
0.2
Concentration in ether layer 5
 
Given : W = 0.01 Kg
V = 0.1 dm3
V1 = 0.02 dm3
n = 5

1
KV
Amount un extracted W
KV V
 
  

 
0.2 0.1
0.01
0.2 0.1 0.02
 

  
 
 
= 3.125 x 10-4
Kg
Hence the amount extracted = 0.01 – 3.125 x 10-4
Kg.
= 9.6874 x 10-3
Kg