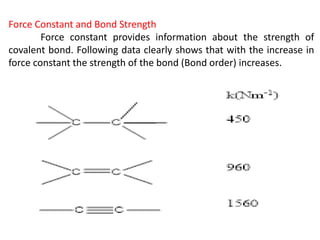
This document discusses the relationship between vibrational frequency and the force constant of a covalent bond. It states that for a diatomic molecule acting as a simple harmonic oscillator, the restoring force is proportional to displacement, as described by Hooke's Law. It then provides the equation relating vibrational frequency, force constant, and reduced mass. Several examples are given of calculating force constants from given vibrational frequencies and reduced masses. The document also notes that a higher force constant corresponds to a stronger covalent bond.

1. Dr. Y. S. THAKARE
M.Sc. (CHE) Ph D, NET, SET
Assistant Professor in Chemistry,
Shri Shivaji Science College, Amravati
Email: yogitathakare_2007@rediffmail.com
B Sc- III Year
SEM-V
PAPER-III
PHYSICAL CHEMISTRY
UNIT- VI
Vibrational Spectroscopy
OR
Infra Red Spectroscopy (IR)
24-November -20 1

2. Relationship between vibrational (or Oscillational) frequency and
force constant of a covalent bond
Diatomic molecule may be considered as a simple vibrating harmonic
oscillator. In such oscillator, the restoring force is proportional to the
displacement of the atom from it`s original position (Hook’s law).
According to Hook’s Law
F 𝛼 𝑋 OR F = 𝑘 𝑋 OR k =
𝐹
𝑋

3. Now, k =
𝐹
𝑋
OR Force constant =
𝑅𝑒𝑠𝑡𝑜𝑟𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒
𝑑𝑖𝑠𝑝𝑙𝑎𝑐𝑒𝑚𝑒𝑛𝑡
The restoring force per unit displacement is called as force constant. It
is related to the vibrational frequency by the equation.
ω𝑜𝑠𝑐 =
1
2π
k
μ
OR ω𝑜𝑠𝑐
2
=
1
4𝜋2 ×
𝑘
μ
k = 4π2μ𝜔𝑜𝑠𝑐
2
Where, µ = reduced mass =
m1m2
m1+m2
where, m1 = mass of one atom,m2 = mass of another atom,
𝜔𝑜𝑠𝑐 = 𝐶 ω𝑜𝑠𝑐
k = 4π2μ𝐶2 ω𝑜𝑠𝑐
2
ω𝑜𝑠𝑐 = vibrational frequency in term of wave no. (in cm-1);
C = velocity of light.
Thus, if 𝜔𝑜𝑠𝑐 is known, the force constant of a bond can be calculated.
The unit of k is dyne/cm. in CGS system while S.I. unit is newton/meter
(Nm-1).

4. Important terms
1. ω𝑜𝑠𝑐 =
1
2π
k
μ
2. k = 4π2
μ𝜔𝑜𝑠𝑐
2
3. 𝜔𝑜𝑠𝑐 = 𝐶 ω𝑜𝑠𝑐
4. μ =
m1m2
m1+m2
5. k = 4π2μ𝐶2 ω𝑜𝑠𝑐
2
6. 𝐶 = 𝑉𝑒𝑙𝑜𝑐𝑖𝑡𝑦 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡 = 3 × 108𝑚𝑆−1

5. Problems
Example 1 : Calculate the force constant of NO molecule if its
fundamental vibrational frequency is 1.876 x 103 cm-1. The reduced
mass of the molecule is 1.24 x 10-26 kg.
Solution :
Given that
K= ?
ω= 1.876 x 103 cm-1 =1.876 x 103 x 102 m-1 = 1.876 x 105 m-1
μ = 1.24 x 10-26 kg
𝐶 = 3 × 108𝑚𝑆−1
Π = 3.14
We know that
k = 4π2μ𝐶2 ω𝑜𝑠𝑐
2
=4 x (3.14)2 x 1.24 x 10-26x (3 × 108)2× (1.876 × 105)2
=1549Nm-1
1m = 100 cm
1m-1 =10-2cm-1
1cm-1=102m-1

6. Example 2 : Calculate the force constant of HCl, if its vibrational
frequency is 8.667 x 1013 sec-1. Reduced mass of HCl is 1.6277 x 10-
27kg.
Solution :
Given that
K= ?
𝝎 = 8.667 x 1013 sec-1 μ = 1.6277 x 10-27 kg
𝐶 = 3 × 108𝑚𝑆−1
Π = 3.14
We know that
k = 4π2μ𝜔𝑜𝑠𝑐
2
= 4 x (3.14)2 x 1.6277 x 10-27 × (8.667 × 1013)2
= 482.2 Nm-1

7. Example 3 : Calculate the force constant of HI if its vibrational
frequency is 6.6 x 1013 sec-1. Reduced mass of HI is 1.648 x 10-27kg.
Solution :
Given that
K= ?
𝝎 = 6.6 x 1013 sec-1
μ = 1.648 x 10-27kg
𝐶 = 3 × 108𝑚𝑆−1
Π = 3.14
We know that
k = 4π2μ𝜔𝑜𝑠𝑐
2
= 4 x (3.14)2 x 1.648 x 10-27kg × (6.6 × 1013)2
= 283.1 Nm-1

8. Example 4. Calculate the wave number of stretching vibration of a C=C bond.
Given
i) k = 1000Nm-1 ii) mC = 12 amu iii) C = 3 x 1010 cms-1
Solution :
Given that
K= 1000Nm-1
𝒎𝒄 = 12 amu
𝐶 = 3 × 108𝑚𝑆−1
Π = 3.14
We know that
ν =
1
2π C
k
μ
μ =
m1m2
m1+m2
=
12×12
12+12
= 6𝑎𝑚𝑢 = 6 × 1.66 × 10−27
= 9.96 × 10−27
𝑘𝑔
ν =
1
2 × 3.14 × 3 × 108
1000
9.96 × 10−27
ν = 0.01678 × 10−8

9. Force Constant and Bond Strength
Force constant provides information about the strength of
covalent bond. Following data clearly shows that with the increase in
force constant the strength of the bond (Bond order) increases.