1. ЛАПЛАСЫН ХУВИРГАЛТ
Pierre Simon Laplace (1749-1827)

2. Лекцийн хураангуй
 Удирдлагын системийн сонгомол онолын суурь
болсон Лапласын хувиргалтыг энэ бүлэгт судална.
Удирдлагын шугаман системийн динамик үйл
явцыг давтамжийн мужид тодорхойлдогоороо энэ
арга нь маш чухал хэрэгсэл юм. Лапласын
хувиргалт хэрэглэн дифференциал тэгшитгэл
бодох тул Лапласын шууд болон урвуу хувиргалт
хийхэд байнга хэрэглэгдэх үндсэн теорем, шинж
чанаруудыг авч үзнэ.
I.LI350
2

3. Дэд бүлгүүд
 Лапласын хувиргалтын тодорхойлолт
 Лапласын шууд болон урвуу хувиргалтын
харгалзуулалт
 Лапласын хувиргалт хэрэглэн шугаман
дифференциал тэгшитгэл бодох
 Нэгж импульс, нэгж үсрэлтийн функцийн
Лапласын хувиргалт
I.LI350
3

4. Лапласын хувиргалт
 Тогтмол коэффициенттой шугаман дифференциал
тэгшитгэл бодох чухал хэрэгсэлийн нэг нь
Лапласын хувиргалт юм. Шугаман дифференциал
тэгшитгэлийг алгебр тэгшитгэл болгон
хувиргадагт Лапласын хувиргалтын давуу тал
оршино.
I.LI350
4

5. Лапласын хувиргалтын
тодорхойлолт
 Хугацааны мужид тодорхойлогдох
функцийг
комплекс тоон мужид тодорхойлогдох
функц
болгох интеграл хувиргалтыг Лапласын хувиргалт
гэнэ.
энд
функцийн аргумент нь
тоон хувьсагч байна.
I.LI350
комплекс
5

6. Лапласын хувиргалтын баталгаа
Баталгаа: Эх функц
гэж өгөгдсөн гэе. Энэ эх
функцээс үүсэх дүрс функцийг Лапласын
хувиргалтаар хэрхэн олохыг харуулъя. Лапласын
хувиргалтын тодорхойлолт ёсоор
гэж бичнэ. Орлуулах аргыг хэрэглэн энэ интегралыг
бодно.
I.LI350
6

7. үед үүсэх
эх функцийг нэгж үсрэлтийн функц
гэнэ. Түүний дүрс функц нь
I.LI350
7

8. №
Эх функц
Дүрс функц
№
1
11
3
12
4
13
5
14
6
15
7
16
8
17
9
Дүрс функц
10
2
Эх функц
18
I.LI350
8

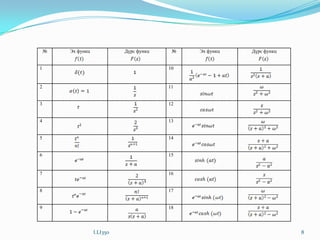
9. Лапласын хувиргалтын үндсэн теоремууд
№
Нийлбэрийн теорем
1
Төсөөтэй чанарын теорем
2
Бодит
теорем
3
Комплекс тооны шилжилтийн
теорем
4
Уламжлалын теорем
тооны
шилжилтийн
үед
5
Комплекс
функцийн
уламжлалын теорем
6
Интегралын теорем
7
Хугацааны муж дахь конволюц
үржвэрийн теорем
8
Анхны утгын теорем
9
Эцсийн утгын теорем
I.LI350
9

10. Уламжлалын тухай теорем баталгаа:
Хэрэв
эх функц болон түүний дүрс функц
Энэ эх функцийн уламжлалын дүрс функц
өгөгдсөн гэж үзье.
болохыг баталцгаая. Лапласын хувиргалтын тодоройлолт ёсоор
Дараах орлуулалтыг хийнэ:
I.LI350
10

11. функцийн хоёрдугаар эрэмбийн уламжлал ийн дүрс функцийг
олбол:
Дараах орлуулалтыг хийнэ:
I.LI350
11

12. Үүнтэй адилханаар гуравдугаар эрэмбийн уламжлал
функцийг олбол:
Дээрх үйлдлийг
удаа хэрэглэвэл
–ийн дүрс функцийг олно:
I.LI350
-ийн дүрс
эрэмбийн уламжлал
12