2. БАГТСАН ОЛОН ӨНЦӨГТ
 Хэрэв гүдгэр олон өнцөгтийн орой бүхэн
нэг тойрог дээр оршиж байвал түүнийг
тойрогт багтсан олон өнцөгт гэнэ.
Харин тойргийг нь олон өнцөгтийг
багтаасан тойрог гэнэ.

3. А3
А2
А1
А4
А5
А6
А7
А8

4. БАГТААСАН ОЛОН ӨНЦӨГТ
 Хэрэв гүдгэр олон өнцөгтийн тал бүр нэгэн
тойрогт шүргэсэн байвал түүнийг тойргийг
багтаасан олон өнцөгт гэнэ. Харин тойргийг нь
олон өнцөгтөд багтсан тойрог гэнэ

5. Багтаасан олон
өнцөгтийн аль ч
талын шүргэлтийн
цэгт татсан радиус
нь уул талдаа
перпендикуляр
байна.

6. ЗӨВ ОЛОН ӨНЦӨГТӨД БАГТСАН, БАГТААСАН ТОЙРГИЙН РАДИУС
ОЛОХ АРГА
а тал бүхий зөв n өнцөгтийг багтаасан ба багтсан тойргийн радиус харгалзан
R , r байна.
Олон өнцөгтийн бүх өнцгүүдийн нийлбэр 180(n-2) тул зөв олон өнцөгтийн
нэг өнцөг байна.
 Гурвалжин AOB-н суурийг

=
A
B
C
O
a/2

7.  Зөв гурвалжин
n=3 үед иймд
 Зөв дөрвөн өнцөгт буюу квадрат
n=4 үед иймд
 Зөв зургаан өнцөгт
n=6 үед , ,

8.  Зөв олон өнцөгтийг багтаасан тойргийн төвөөс
түүний тал хүрэх зайг уул зөв олон өнцөгтийн
анофем гэнэ.

9. ГУРВАЛЖИНГ БАГТААСАН ТОЙРОГ
Асуулт:
 Гурвалжинг багтаасан тойргийн төв хаана байх вэ?
Хариулт:
 Талуудын дундаж дээр босгосон перпендукляруудын
огтолцлын цэг нь багтаасан тойргийн төв болно.

10. Багтаасан тойргийн радиусыг R үсгээр
тэмдэглэнэ

11. ТЕОРОМ 1(ТОЙРОГТ БАГТСАН ГУРВАЛЖНИЙ ХУВЬД)

А
C
B
K
β
β
R

12. ТЕОРОМ 2(ТОЙРОГТ БАГТСАН ТЭГШ ӨГЦӨГТ ГУРВАЛЖНИЙ ХУВЬД)

B
A C
O
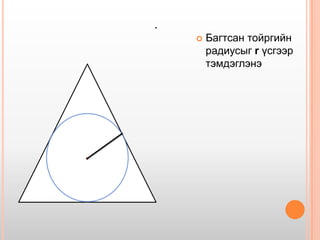
R
R R
a
b
c

13. ГУРВАЛЖИНД БАГТСАН ТОЙРОГ
 Асуулт: Багтсан тойргийн төв хаана байх вэ?
 Хариулт: Багтсан тойргийн төв нь гурвалжны 3
оройгоос татсан биссекрисүүдийн огтлолцлын
цэг байна.

14. .
 Багтсан тойргийн
радиусыг r үсгээр
тэмдэглэнэ

15. ТЕОРОМ 3(ТОЙРГИЙГ БАГТААСАН ГУРВАЛЖНИЙ ХУВЬД)

O
B
CA
L
N

16. ТЕОРОМ 4(ТОЙРГИЙГ БАГТААСАН ТЭГШ ӨГЦӨГТ ГУРВАЛЖНИЙ
ХУВЬД)

A
B
C
L
M
N
Or
r
r

17. ТОЙРГИЙГ БАГТААСАН ДӨРВӨН ӨНЦӨГТ
Чанар1:
AD+BC=AB+DC байна.
MA=AN=т
NB=BK=а
KC=FC=л
DF=MD=х
AD+BC=AB+DC
Т+а+л+х=т+а+л+х
Талх=талх буюу
AD+BC=AB+DC
Эсрэг орших талуудын
нийлбэр нь хоорондоо
тэнцүү.
N
K
F
M
т
а
л
лх
х
B
C
A т а

18. ПТОЛЕМИЙН ТЕОРЕМ
AB*CD+BC*AD= AC*BD
ac+bd =d1 d2 гэдгийг батлая
ABD-с
 d2
2= a2 + d 2 - 2ad Cos
 гурвалжин BCD-с
 d2
2= b2+c2 -2bcCos(180-)
 d2
2= b2+c2 +2bcCos болно
 d2
2= a2 + d 2 - 2ad Cos(bc)
 d2
2= b2+c2 +2bcCos (ad)
 bcd2
2+ add2
2= a2bc+d2bc+b2ad+c2ad
 d2
2(bc+ad)= ab(ac+bd)+ dc(bd+ac)
 d2
2(bc+ad)=(ac+bd)(ab+dc) (1)
 d1
2=d2+c2-2dc*Cos
 d1
2= a2+b2-2ab*Cos(180-)
 d1
2= a2+b2+2ab*Cos болно
 d1
2(ab+cd)= d2ab+c2ab+a2cd+b2 cd
 d1
2(ab+cd)= (ad+bc)(bd+ac) ( 2 )
 1 ба 2ийг гишүүнчлэн үржүүлье
 d2
2(bc+ad)* d1
2(ab+cd)=( ac+bd)(ab+dc)
(ac+bd)(ab+dc)
 d1
2* d2
2 = (ac+bd) 2
 d1d2= ac+ bd гэж батлагдав.
d1
d2
A
B
C
D
a
c
b
d